Экзаменационный билет № 11

1. Распределение скоростей молекул газа. Закон распределения скоростей Максвелла. Принцип детального равновесия. Закон распределения Больцмана. Энтропия и вероятность. Метод наиболее вероятного распределения в статистике Больцмана. Статистика Ферми-Дирака, Бозе-Эйнштейна. Теорема Нернста. Квантовая теория теплоемкости Эйнштейна.

2. Статистическая термодинамика квантовых идеальных одноатомных газов. Распределение Бозе-Эйнштейна и Ферми-Дирака. Сопоставление распределений М.-Б., Б.-Э. и Ф.-Д. Вырождение квантовых газов. Теплоёмкость твёрдых тел.

1. Распределение скоростей молекул газа. Закон распределения скоростей Максвелла. Принцип детального равновесия. Закон распределения Больцмана. Энтропия и вероятность. Метод наиболее вероятного распределения в статистике Больцмана. Статистика Ферми-Дирака, Бозе-Эйнштейна. Теорема Нернста. Квантовая теория теплоемкости Эйнштейна.

Распределение по скоростям молекул идеального газа. Максвелл. В одномерном случае распределение молекул идеального газа по одной из компонент скорости, например, 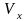описывается нормальным распределением , (1)

где - масса молекулы, - абсолютная температура, 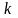постоянная Больцмана.

При этом средняя скорость молекул равна нулю, а стандартное отклонение .

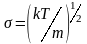Г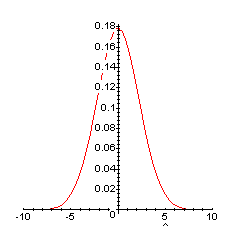 рафик функции (1) имеет вид:

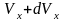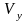Для двумерного случая распределение молекул идеального газа, компоненты скорости которых заключены в интервалы от до и от до 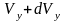имеет вид:

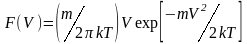, (2) где 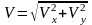; 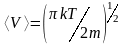- средняя скорость движения молекул; 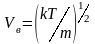- вероятная скорость движения молекул.

В трехмерном случае распределение частиц по величине скорости описывается распределением Максвелла:

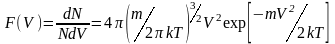, (3) где 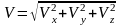; 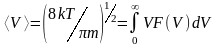- средняя скорость движения молекул; 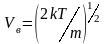- вероятная скорость движения молекул (максимум F(V)). 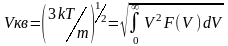- Среднеквадратичная скорость молекул

График функции (3) изображен на рис. 2.

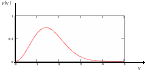Рис. 2

Значение функции распределения имеет смысл доли молекул, скорости которых лежат в пределах V…V+dV.

Интеграл от нормального распределения F(V), взятый в пределах от некоторой скорости V1 до некоторой скорости V2 дает относительное количество (долю) молекул, скорости которых лежат в диапазоне от V1 до V2. Интеграл от нормального распределения F(V) по всем скоростям от 0 до бесконечности дает 1 - все молекулы находятся в данном скоростном диапазоне. Площадь под графиком, ограниченная двумя вертикальными линиями, соответствующими скоростям V1 и V2, равна относительному количеству молекул в данном скоростном диапазоне (от V1 до V2).В любой части системы, содержащей достаточно большое количество молекул в состоянии термодинамического равновесия, справедливо распределение Максвелла для скоростей молекул.

Детального равновесия принцип, общее положение статистической физики, согласно которому любой микроскопический процесс в равновесной системе протекает с той же скоростью, что и обратный ему. Когда система, состоящая из большого числа частиц, находится в равновесии, постоянными во времени остаются лишь физические величины, относящиеся к системе в целом (они называются термодинамическими величинами). В то же время составляющие систему отдельные микрочастицы меняют своё состояние: в равновесной системе происходят столкновения частиц (атомов, молекул и др.), могут протекать химические реакции и т.п. Конечно, чтобы равновесие сохранялось, наряду с любым таким микропроцессом должен осуществляться и обратный ему (т. к., действуя лишь в одном направлении, микропроцесс может привести к изменению состояния системы в целом). Детального равновесия принцип утверждает, что скорость любого микропроцесса (число происходящих за 1 сек событий этого микропроцесса) совпадает в состоянии равновесия со скоростью обратного ему процесса. Скорость при этом трактуется статистически — как среднее по большому числу одинаковых микропроцессов.

В квантовой теории Детального равновесия принцип состоит в равенстве вероятностей прямого и обратного процессов. Этими процессами могут быть квантовые переходы, реакции между элементарными частицами и т.д.

Распределение Больцмана.

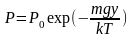
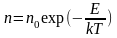Энтропия и вероятность. Им. Т.С., в кот определены суммарная энтропия, стат вес. Проделано отверстие, мол-лы вылетают. – процесс необратимый. Энтроп. и стат вес увеличив.,

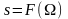
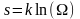
Статистика Ф.-Д., Б.-Э. Волновая функция системы бозонов симметрична, а фермионов – антисимметрична относительно перестановки любой пары частиц. Волновая функция квантового идеального газа представляется произведением волновых функций отдельных частиц и полностью определяется заданием чисел заполнения n_k каждого к-го одночастичного состояния. Требование антисимметрии волновой функции системы фермионов приводит к тому, что они удовлетворяют принципу Паули: в заданном квантовом состоянии может находиться не более одной частицы, т.е. n_k=0; 1. В каждом одночастичном состоянии бозе-газа может находиться любое число частиц: n_k=0;1;2,…N, где N – общее число частиц в системе.

Распределение частиц по одночастичным квантовым состояниям зависит от того, являются ли частицы бозонами или фермионами. В соответствии с этим существуют две квантовые статистики: статистика Бозе-Эйнштейна (для бозонов) и статистика Ферми-Дирака (для фермионов). Функция распределения по квантовым состояниям обоих классов частиц имеет вид:

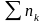
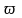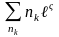
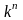= (n_k) = ^k / 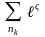^k 1. Распределение бозе-частиц по состояниям называется распределением Бозе-Эйнштейна: = 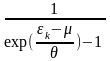оно было установлено в 1924 г. Распределение частиц по энергиям найдем, умножив на число g_k микросостояний с энергией 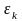: ( ) = 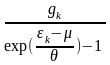2. Распределение Ферми-Дирака Среднее число ферми-частиц в к-ом состоянии равно: = 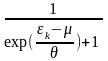Распределение электронов по эгеогиям (s=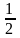 ) будет ( ) =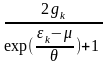 сопоставление распределений М-Б, Б-Э и Ф-Д: все эти три функции распределения идеальных газов можно записать в едином виде: = 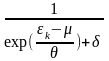, (1) где 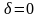для распределения М-Б, 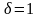для распределения Ф-Д, 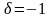для распределения Б-Э. На рис приведены графики этих функций распределения. Из (1 ) видно, что распределения Б-Э и Ф-Д переходят в распределение М-Б, т.е. газ становится классическим, ес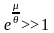ли . (2) Если 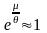, то функция распределения газа отличается от максвелл-больщмановской и говорят, что газ вырожден. Величина 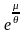называется фактором вырождения, выражение (2) – критерием невырожденности, а противоположные неравенства – критерием сильного вырождения.

Теплоемкость твердых тел рассчитывается по формуле Дюлонга и Пти: 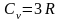Твердое тело рассматривается как совокупность N независимых атомов, колеблющихся с одной и той же частотой ν. Однако средняя энергия, приходящаяся на одну степень свободы, полагается равной не КТ, а вычисляется по формуле Планка для средней энергии линейного осциллятора: 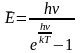(1)энергия грамм-атома, имеющего 3N степеней свободы, равна: 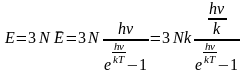(2), величину 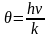, имеющего размерность температуры, Эйнштейн назвал характеристической температурой тела. Следовательно 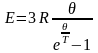, дифференцируя по температуре, получим

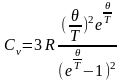
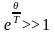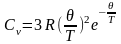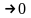
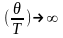При низких температурах (Т<<θ), , вследствие чего единицей в знаменателе можно пренебречь и записать: При Т , а

Теорема Нернста: когда система приходит к температуре абсолютного нуля, то энтропия приходит к 0.следовательно достигнуть абс. 0 нельзя.

2. Статистическая термодинамика квантовых идеальных одноатомных газов. Распределение Бозе-Эйнштейна и Ферми-Дирака. Сопоставление распределений М.-Б., Б.-Э. и Ф.-Д. Вырождение квантовых газов. Теплоёмкость твёрдых тел.

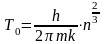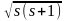При температурах Т<Т₀ ( ) система частиц становится квантовой. Квантовые частицы помимо волновых свойств обладают собственным (спиновым) механическим моментом. Его величина равна h ,где спин s – целое (включая нуль) или полуцелое положительное число, определяемое природой частиц. Таким образом, состояние квантовой частицы данного типа определяется волновой функцией Ψ(x,y,z) и спиновым числом m_s (характеризующим одно из возможных значений проекций спинового момента на фиксированную ось). Возможны 2s+1 состояний с заданной волновой функцией, отличающейся ориентацией спина.

Так как в отсутствие магнитного поля энергия частицы не зависит от ориентации спина, то наличие спина увеличивает число квантовых состояний с заданной энергией в 2s+1 раз. В зависимости от того, является ли спин целым или полуцелым, частицы делятся на два класса: бозе-частицы, или бозоны (с целым спином), и ферми-частицы, или фермионы (с полуцелым спином). Бозонами являются фотон (s=1), π- и К-мезоны (s=0). Большинство элементарных частиц (электроны, протоны, нейтроны и др.) имеют спин s = и являются фермионами.

Спин сложной частицы определяется числом входящих в нее фермионов. Если это число четное (Н, Н₂, Не⁴), то сложная частица является бозоном, если нечетное (D, HD) – фермионом.

Волновая функция системы бозонов симметрична, а фермионов – антисимметрична относительно перестановки любой пары частиц. Волновая функция квантового идеального газа представляется произведением волновых функций отдельных частиц и полностью определяется заданием чисел заполнения n_k каждого к-го одночастичного состояния. Требование антисимметрии волновой функции системы фермионов приводит к тому, что они удовлетворяют принципу Паули: в заданном квантовом состоянии может находиться не более одной частицы, т.е. n_k=0; 1. В каждом одночастичном состоянии бозе-газа может находиться любое число частиц: n_k=0;1;2,…N, где N – общее число частиц в системе.

Распределение частиц по одночастичным квантовым состояниям зависит от того, являются ли частицы бозонами или фермионами. В соответствии с этим существуют две квантовые статистики: статистика Бозе-Эйнштейна (для бозонов) и статистика Ферми-Дирака (для фермионов). Функция распределения по квантовым состояниям обоих классов частиц имеет вид:

= (n_k) = ^k / ^k 1. Распределение бозе-частиц по состояниям называется распределением Бозе-Эйнштейна: = оно было установлено в 1924 г. Распределение частиц по энергиям найдем, умножив на число g_k микросостояний с энергией : ( ) = 2. Распределение Ферми-Дирака Среднее число ферми-частиц в к-ом состоянии равно: = Распределение электронов по эгеогиям (s= ) будет ( ) = сопоставление распределений М-Б, Б-Э и Ф-Д: все эти три функции распределения идеальных газов можно записать в едином виде: = , (1) где для распределения М-Б, для распределения Ф-Д, для распределения Б-Э. На рис приведены графики этих функций распределения. Из (1 ) видно, что распределения Б-Э и Ф-Д переходят в распределение М-Б, т.е. газ становится классическим, если . (2) Если , то функция распределения газа отличается от максвелл-больщмановской и говорят, что газ вырожден. Величина называется фактором вырождения, выражение (2) – критерием невырожденности, а противоположные неравенства – критерием сильного вырождения.

Теплоемкость твердых тел рассчитывается по формуле Дюлонга и Пти: Твердое тело рассматривается как совокупность N независимых атомов, колеблющихся с одной и той же частотой ν. Однако средняя энергия, приходящаяся на одну степень свободы, полагается равной не КТ, а вычисляется по формуле Планка для средней энергии линейного осциллятора: (1)энергия грамм-атома, имеющего 3N степеней свободы, равна: (2), величину , имеющего размерность температуры, Эйнштейн назвал характеристической температурой тела. Следовательно , дифференцируя по температуре, получим

При низких температурах (Т<<θ), , вследствие чего единицей в знаменателе можно пренебречь и записать: При Т , а