
- •1.Область применения конструкций из дерева и пластмассы.
- •2.Достоинства древесины как конструктивного материала:
- •3.Строение древесины.
- •4.Влага в древесине. Влажность.
- •5.Форма изменяемости деревянных элементов.
- •6.Прочность древесины и сопротивление её огню.
- •10.Механические свойства древесины.
- •11.Пороки древесины.
- •12.Работа древесины на растяжение, сжатие и поперечный изгиб.
- •13.Работа древесины его смятие, скалывание и раскалывание.
- •14.Влияние влажности на прочность древесины.
- •15.Влияние температуры на прочность древесины.
- •16.Строительная фанера как конструктивный материал.
- •17.Временное, нормативное и расчётное сопротивление древесины.
- •19.Расчёт элементов деревянных конструкций по предельным состояниям.
- •20.Пластмассы.
- •21.Виды конструкторских пластмасс.
- •22.Расчёт центрально растянутых элементов.
- •23.Расчёт центрально сжатых элементов цельного сечения.
- •25.Расчёт деревянных элементов цельного сечения на поперечный изгиб.
- •26.Расчёт деревянных элементов цельного сечения на косой изгиб.
- •27.Расчёт элементов конструкций на внецентренное сжатие и сжатие с изгибом.
- •28.Расчёт элементов деревянных конструкций на растяжение с изгибом.
- •29.Классификация и виды соединений.
- •30,31.Требования, предъявляемые к соединениям.
- •32.Врубки.
- •33.Требования и рекомендации при изготовлении лобовых врубок.
- •34.Расчёт лобовых врубок.
- •35.Нагельные соединения.
- •38.Расчётные формулы для нагельных соединений.
- •39.Клеевые соединения.
- •(39)Требования предъявляемые к клеям.
- •40.Виды клеев.
- •41.При конструкции клеевых соединений следует:
- •42.Соединения на вклеёных стержнях.
- •46.Подвижность связи и её учёт при расчёте составных элементов деревянных конструкций
- •Расчёт составных элементов на поперечный изгиб.
- •Гибкость составных элементов.
- •48.Расчёт элементов составного сечения на сжатие с изгибом.
- •49.Настилы. Покрытия.
- •(49).Расчёт элементов настила.
- •50.Прогоны покрытия.
- •Неразрезные прогоны.
- •Консольно-балочные прогоны.
- •Конструкции из дерева и пластмасс. Клейфанерные балки.
- •53.Расчёт клейфанерных балок с плоской фанерной стенкой.
- •(53).Метод приведённого сечения:
- •54.Особенности конструирования и расчёта клейфанерных балок с волнистой фанерой.
26.Расчёт деревянных элементов цельного сечения на косой изгиб.
Косоизгибаемые элементы –это, как правило, балки и прогоны скатных покрытий. Косым называется изгиб, при котором направление действия усилия не совпадает с направлением одной из главных осей поперечного сечения элемента. В этом случае действующее усилие раскладывается по направлению главных осей в сечении, а затем находят изгибающие моменты, действующие в этих плоскостях.
В данном случае нормальные напряжения находят по формуле δu=Мx/Wx+Мy/Wy≤Ru,
Вертикальная нагрузка, например, равномерная «q» и изгибающий момент от неё М при косом изгибе элемента прямоугольного сечения под углом α раскладывается на нормальные и тангенсальные (скатные) составляющие вдоль осей сечений.
Относительно этих же осей определяют моменты сопротивления W и моменты инерции Y сечений:
δu=Мx/Yx×y1,2, Yx=Ycosα
Косоизгибаемые элементы, так же необходимо проверять по прогибам. Эти прогибы вычисляют с учётом геометрической суммы прогибов относительно каждой оси по формуле:
![]() ,
,
![]() ,
,
27.Расчёт элементов конструкций на внецентренное сжатие и сжатие с изгибом.
Сжатоизгибаемые элементы работают одновременно на сжатие и изгиб. Например, это элементы верхнего пояса ферм, в которых кроме сжатия действует ещё изгиб от межузловой нагрузки от веса покрытия.
Элементы верхнего пояса ферм могут так же испытывать внецентренное сжатие, когда на элементы действует поперечная нагрузка и продольная сила (сжимающая) действует на элемент с эксцентриситетом. Мало того, эксцентриситет в элементе может быть различным, т.е. (l1+l2)/2
На сжатие с изгибом так же работает верхний пояс арок.
На внецентренное сжатие или сжатие с изгибом работают так же стойки с колоннами. Изгибающий момент может создаваться: а) внецентренно приложенной сжимающей силой, тогда элемент называют внецентренно сжатым; б) поперечной нагрузкой.
При расчёте сжато изгибаемых деревянных стержней применяют теорию краевых напряжений, предложенную К.С. Завриевым. В соответствии с этой теорией несущая способность стержня считается исчерпанной в тот момент, когда краевое напряжение сжатия делается равным расчётному сопротивлению сжатию. Эта теория принята в действующих нормах проектирования. Эта теория приближённая, мене точная, чем теория устойчивости, однако, даёт более простое решение, весьма удобна для проектировщиков.
Рассмотрим стержень нагруженный продольной нагрузкой N и поперечной нагрузкой Q. При расчёте таких элементов не в коем случае нельзя использовать принцип независимости действия сил.
N/F+M/W , т.е. когда суммируют напряжения (нормальные) от действия продольных сил и напряжение от действия изгибающего момента. Потому что наличие одной нагрузки (напряжения) изменяет характер напряжений от действия другой нагрузки. В сечении сжато изгибаемого элемента действуют продольные сжимающие силы N, от этих сил возникают равномерные напряжения сжатия и изгибающий момент М, от которого появляются сжимающие и растягивающие напряжения, которые максимальны в крайних волокнах и равны нулю на нейтральной оси.
Напряжения сжатия, возникающие в сечении древесного элемента, складываются на напряжение сжатия и растяжения – вычитаются. Максимальное сжимающее напряжение возникает в крайних волокнах сечения в месте действия максимального изгибающего момента. Разрушение сжато изгибаемого элемента начинается с потери устойчивости сжатых волокон, что обнаруживается появлением складок и повышенными прогибами. ∞Такое разрушение частично пластично, т.к. жёсткость стержня не является ∞, то он под влиянием изгибающего момента прогибается. При этом центрально приложенная сжимающая сила, теперь уже будет иметь эксцентриситет = деформации стержня от момента. И, таким образом, создаёт дополнительный сжимающий момент. Появление дополнительного момента от нормальной силы увеличивает деформацию стержня, что приводит к ещё большему возрастанию момента. Такое наращивание дополнительного момента и прогибов будет продолжаться некоторое время и затем затухнет. В основу метода Завриева положено:
1.Независимо от характера распределения нагрузки, стержень всегда изгибается по закону синусоиды. В действительности это возможно, если нагрузка распределяется по синусоиде.
2.Стержень работает упруго.
3.Напряжения (опасные) достигают предела прочности при сжатии.
Вообще, полный прогиб стержня и уравнение кривой неизвестны, поэтому непосредственно формулой краевых напряжений пользоваться нельзя.
![]() (1),
(1),
Полный изгибающий момент стержня равен
![]() (2),
(2),
В обоих уравнениях есть 3 неизвестных: δс, у, МХ.
Всякую кривую аналитически можно выразить в виде ряда который при этом должен быть быстросходящимся и удовлетворять краевым значениям. Таким является тригонометрический ряд:
![]()
При симметричной загрузке первый член
ряда даёт точность 95-97%. Для упрощения
решений считают нагрузку симметричной.
Тогда можно ограничится первым частным
ряда
![]()
С появлением этого уравнения мы получаем
4 недостающее неизвестное f1.
Из курса строительной механики видно,
что вторая производная уравнения кривой
деформирования равная
![]()
После дифференцирования получим:
![]() ,
следовательно
,
следовательно
![]() .
.
Если из этого уравнения выделить МХ
и подставить в уравнение МХ=Мq+Мy,
то после преобразований, имея в виду
что
![]() и
и
![]() и Ymax=f,
то получим следующее выражение:
и Ymax=f,
то получим следующее выражение:
![]()
Найденная зависимость позволяет решать
вопрос об определении напряжения. Для
этого значение f1
подставим в выражение:
![]()
![]()
После преобразования получим:
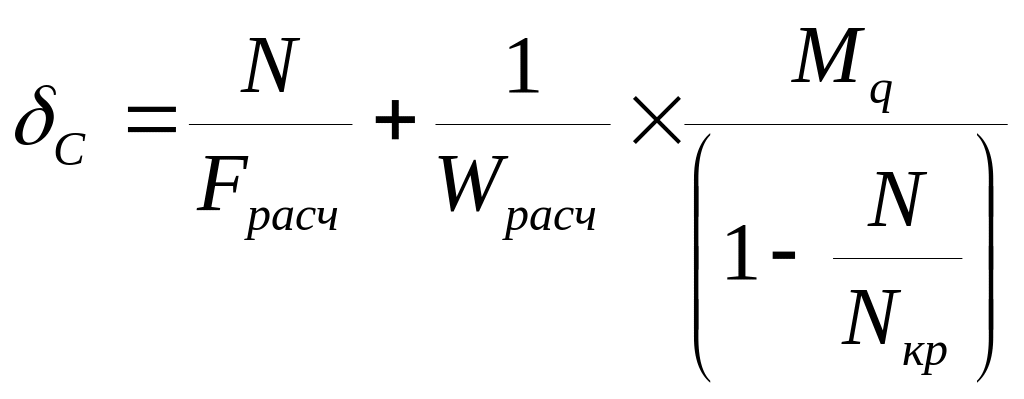 , где
, где
![]()
![]() -
коэффициент, учитывающий дополнительный
изгибающий момент от продольной силы
при деформации стержня. Применим при
значении от «0» до «1».
-
коэффициент, учитывающий дополнительный
изгибающий момент от продольной силы
при деформации стержня. Применим при
значении от «0» до «1».
Nкр=φ×RС×Fбр.
Окончательно выражение можно записать
в виде:
![]() ,
где
,
где
![]() ;
;![]() ,
т.к. 0<
<1.
,
т.к. 0<
<1.
Если =0, то N=φ×F×R=0?
Если =1, то N=0 – продольной силы нет
Если
≤0,
то (невозможно)
![]()
В связи с тем, что значение коэффициента
пропорционального изгиба при вычисление
значения
всегда определяется по следующей
формуле: φ=3000/λ2, то при малых
изгибающих напряжениях
![]() ,
,
![]() ,
то работа стержня близка к условиям
продольного изгиба и формула даст
неправильный результат. В этом случае
стержень надо рассчитывать на продольный
изгиб без учёта изгибающего момента.
При определении прогиба сжато изгибаемого
элемента надо учитывать влияние
дополнительного момента от продольной
силы f=f0/
,
,
то работа стержня близка к условиям
продольного изгиба и формула даст
неправильный результат. В этом случае
стержень надо рассчитывать на продольный
изгиб без учёта изгибающего момента.
При определении прогиба сжато изгибаемого
элемента надо учитывать влияние
дополнительного момента от продольной
силы f=f0/
,
![]()
Общая формула
Далее по действующему СНиПу рекомендуется следующее уточнение. При несимметричном нагружении, нагрузку раскладывают на симметричную и кососимметричную.
![]()
Далее СНиП рекомендует домножать коэффициент влияния продольной силы на изгибающий момент: kН –поправочный коэффициент, зависящий от формы эпюры изгибающего момента.
kН =αн+ (1-αн), где αн =0,81 –при прямоугольной эпюре, αн =1,22 - при треугольной эпюре.
Этот поправочный коэффициент даёт уточнение в 5%. Также при необходимости сжато изгибаемые элементы необходимо проверять на прочность по скалывающим напряжениям: τ≤Rск;
Сжато изгибаемый элемент должен быть
так же проверен на устойчивость плоской
формы деформирования.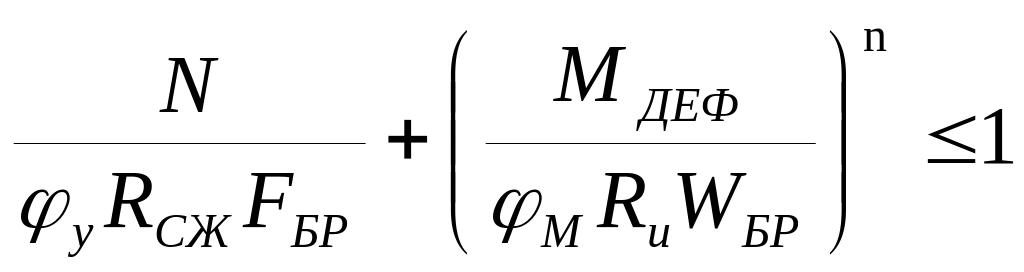 ,
где φу-коэффициент продольного
изгиба с учётом работы стержня из
плоскости, φу =3000/λ2- для
гибкости участка элемента расчётной
длины lp
из плоскости деформирования, φМ-коэффициент
продольного изгиба от действия изгибающего
момента, FБР - площадь
брутто, с максимальными размерами
сечения элемента на участке lp,
WБР – максимальный
момент сопротивления (брутто) на участке
lp, n
– коэффициент, зависящий от закрепления
растянутой зоны из плоскости деформирования
n=2 – без закрепления
растянутой зоны из плоскости, n=
1 – для элементов имеющих такие
закрепления.
,
где φу-коэффициент продольного
изгиба с учётом работы стержня из
плоскости, φу =3000/λ2- для
гибкости участка элемента расчётной
длины lp
из плоскости деформирования, φМ-коэффициент
продольного изгиба от действия изгибающего
момента, FБР - площадь
брутто, с максимальными размерами
сечения элемента на участке lp,
WБР – максимальный
момент сопротивления (брутто) на участке
lp, n
– коэффициент, зависящий от закрепления
растянутой зоны из плоскости деформирования
n=2 – без закрепления
растянутой зоны из плоскости, n=
1 – для элементов имеющих такие
закрепления.
