Задачи для самостоятельного решения

4.1. Изменить порядок интегрирования в повторном интеграле

.

4.2. Расставить различными способами пределы интегрирования в тройном интеграле , где - трехмерная область, ограниченная поверхностями и .

Замена переменных в двойном и тройном интегралах

Если замкнутая область плоскости преобразуется в замкнутую область плоскости при помощи непрерывно дифференцируемых функций , тогда модуль якобиана преобразования равен коэффициенту искажения меры и двойной интеграл преобразуется следующим образом

.

Если область преобразуется в область при помощи непрерывно дифференцируемых функций , , , тогда в тройном интеграле замена переменных осуществляется по формуле

.

При вычислении двойных интегралов часто используется переход к полярной системе координат или к обобщенной полярной системе координат . Якобианы в этом случае равны и , соответственно.

В трехмерном случае часто используется переход к цилиндрическим координатам с якобианом или к сферическим координатам , , с якобианом .

Пример 4.7. Вычислить двойной интеграл , где область интегрирования удовлетворяет неравенству .

Р ешение. Область интегрирования представляет собой кольцо, образованное двумя окружностями с центром в начале координат и радиусами 1 и 2. Так как область интегрирования образована двумя окружностями, и подынтегральная функция содержит двучлен вида , вычисление двойного интеграла значительно упростится при переходе к полярной системе координат: , . При замене переменных подынтегральная функция преобразуется к виду , а элементарная площадка с учетом якобиана (коэффициента преобразования площади) преобразуется к виду . Расставим пределы интегрирования в повторном интеграле. В качестве внутреннего возьмем интеграл по . Внутри области при произвольном поместим отрезок, параллельный радиусу вектору. Один конец отрезка лежит на внутренней окружности радиуса 1, а второй – на внешней окружности радиуса 2. Поворачивая отрезок на угол против часовой стрелки от до , мы заметаем все точки области . Таким образом, , следовательно

.

Однократные интегралы в полученном повторном интеграле независимы, потому их можно вычислять в произвольном порядке

.

Пример 4.8. Вычислить тройной интеграл , где область интегрирования ограничена поверхностями , , .

Решение. Область интегрирования снизу ограничена плоской поверхностью , сверху конической поверхностью , с боков цилиндрической поверхностью , поэтому тройной интеграл сведем к однократному интегралу по и к двойному интегралу по проекции области на плоскость - кругу единичного радиуса . Вычисляем интеграл по и получаем двойной интеграл . Для вычисления двойного интеграла по кругу единичного радиуса переходим к полярной системе координат , . Учитывая, что и , получаем .

Для вычисления тройного интеграла в данном примере можно было перейти к цилиндрической системе координат , , и тройной интеграл сразу свести к трем однократным

.

Заметим, что при переходе к цилиндрической системе координата не изменяется, а координаты и изменяются также как при переходе к полярной системе координат, поэтому коэффициент искажения объема и коэффициент искажения площади в этих преобразованиях одинаковы и равны .

Пример 4.9. Вычислить тройной интеграл , где область интегрирования определяется неравенством .

Решение. Переписываем неравенство в виде и определяем, что область интегрирования представляет собой замкнутый (содержащий границу) шар радиуса с центром, смещенным по оси на . Переходим к сферическим координатам , , с якобианом . При этом подынтегральная функция принимает вид , элемент объема с учетом якобиана равен , а неравенство, определяющее область интегрирования, приобретает вид . Область интегрирования в сферических координатах можно представить в виде , поэтому тройной интеграл сводим к трем однократным

.
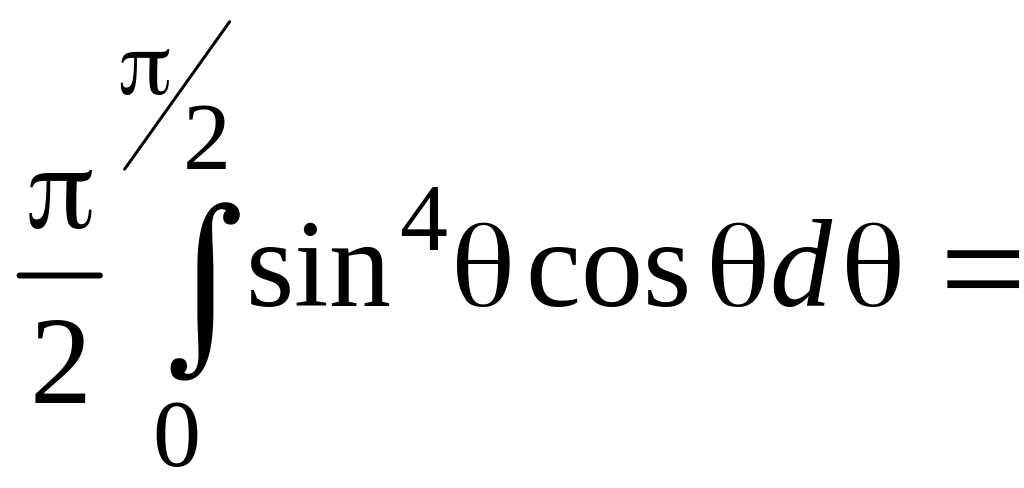
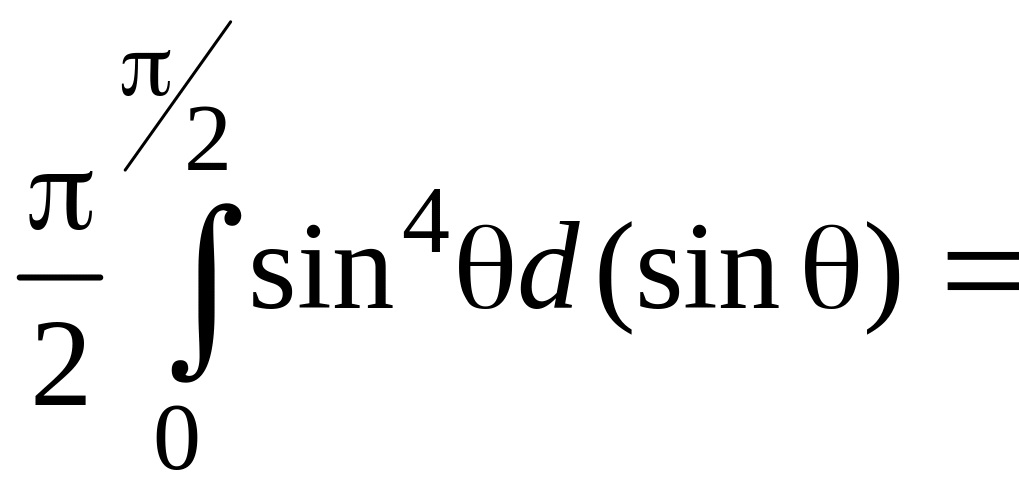