
Кратные интегралы
Пусть непрерывная
функция
![]() задана на замкнутом, интегрируемом по
Жордану, множестве
задана на замкнутом, интегрируемом по
Жордану, множестве
![]() в плоскости
в плоскости
![]() и пусть
и пусть
![]() -
произвольное разбиение множества
на ячейки
-
произвольное разбиение множества
на ячейки
![]() с мерой (площадью)
с мерой (площадью)
![]() .
Диаметром ячейки
.
Диаметром ячейки
![]() назовем максимальное расстояние между
точками множества
назовем максимальное расстояние между
точками множества
![]() .
Выберем в каждой ячейке произвольную
точку
.
Выберем в каждой ячейке произвольную
точку
![]() и составим интегральную сумму
и составим интегральную сумму
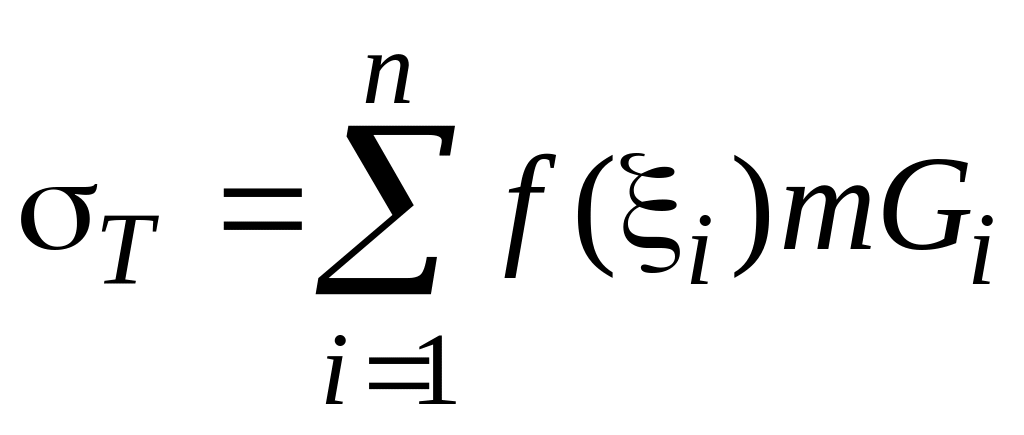 .
.
Возьмем предел данной интегральной суммы при стремлении максимального диаметра ячеек к нулю. Этот предел, если он существует и конечен, не зависит от разбиения и от выбора точек , называется двойным интегралом или интегралом Римана от функции по множеству и обозначается
 .
.
Двойной интеграл
можно вычислить с помощью повторного
интеграла. Если множество
задано неравенствами
![]() ,
где
,
где
![]() и
и
![]() - непрерывные на отрезке
- непрерывные на отрезке
![]() функции, то двойной интеграл сводится
к повторному
функции, то двойной интеграл сводится
к повторному
 ,
,
в котором интеграл
по
![]() будем называть внутренним, а по
будем называть внутренним, а по
![]() - внешним интегралом. Если множество
задано неравенствами
- внешним интегралом. Если множество
задано неравенствами
![]() ,
где
,
где
![]() и
и
![]() - непрерывные на отрезке
- непрерывные на отрезке
![]() функции, то двойной интеграл сводится
к повторному
функции, то двойной интеграл сводится
к повторному
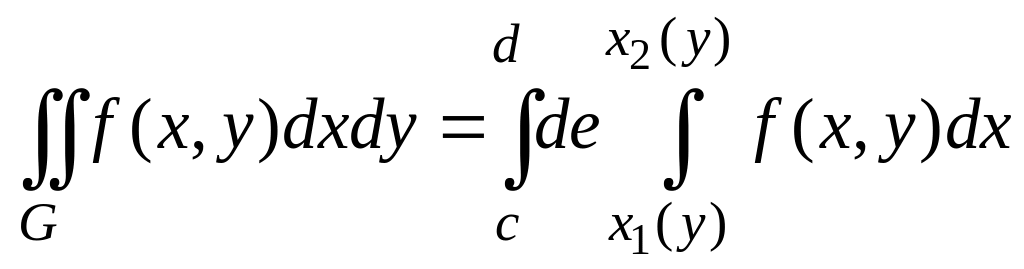 ,
,
в котором интеграл по называется внутренним, а по - внешним интегралом.
Пусть непрерывная
функция
задана на замкнутом, интегрируемом по
Жордану, множестве
![]() пространства
пространства
![]() с
мерами (объемами) ячеек
с
мерами (объемами) ячеек
![]() ,
тогда интеграл Римана от функции
по множеству
называется тройным интегралом и
обозначается
,
тогда интеграл Римана от функции
по множеству
называется тройным интегралом и
обозначается
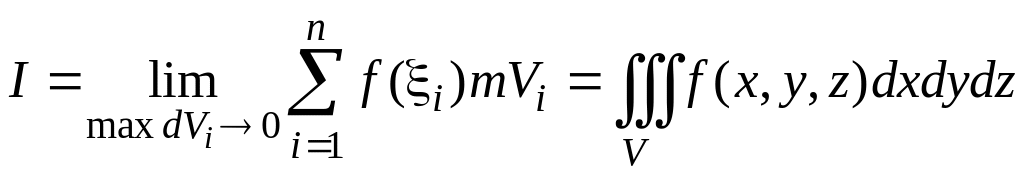 .
.
В декартовой
системе координат вычисление тройного
интеграла сводится к вычислению двойного
интеграла и однократного интеграла.
Если, например, множество
ограничено снизу поверхностью
![]() ,
сверху поверхностью
,
сверху поверхностью
![]() и с боков цилиндрической поверхностью
с образующей параллельной оси
и с боков цилиндрической поверхностью
с образующей параллельной оси
![]() ,
тогда тройной интеграл вычисляется по
формуле
,
тогда тройной интеграл вычисляется по
формуле
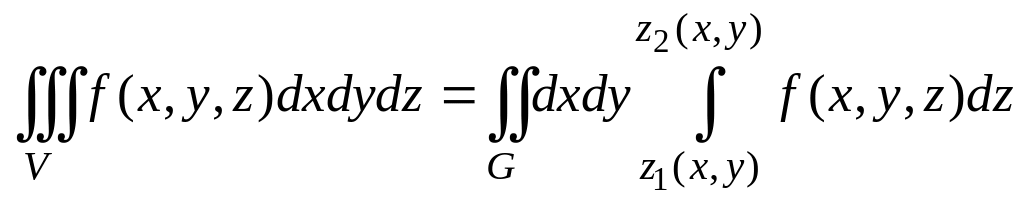 ,
,
где
- проекция множества
на плоскость
![]() .
.
Тройной интеграл
также можно вычислить с помощью трех
однократных интегралов. Если множество
задано неравенствами
,
![]() ,
где
,
,
,
где
,
,
![]() и
и
![]() - непрерывные в соответствующих областях
функции, то тройной интеграл сводится
к виду
- непрерывные в соответствующих областях
функции, то тройной интеграл сводится
к виду
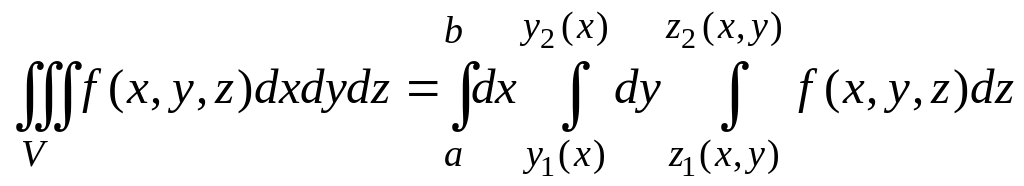 .
.
Пример 4.1. Свести
двойной интеграл
![]() к повторному. Область
определяется уравнениями
к повторному. Область
определяется уравнениями
![]() и
и
![]() .
.
Решение.
Кривые, определяющие границу области
,
пересекаются в точках с координатами
![]() и
и
![]() .
Сначала в качестве внутреннего интеграла
возьмем интеграл по
.
Для этого внутри области
при произвольном значении
.
Сначала в качестве внутреннего интеграла
возьмем интеграл по
.
Для этого внутри области
при произвольном значении
![]() поместим отрезок, параллельный оси
поместим отрезок, параллельный оси
![]() .
.
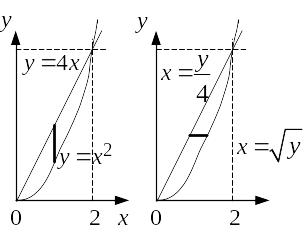
Нижняя координата
отрезка определяется уравнением
,
а верхняя координата уравнением
![]() .
Данный отрезок заметает все точки
области при изменении
от 0 до 2. Таким образом,
.
Данный отрезок заметает все точки
области при изменении
от 0 до 2. Таким образом,
![]() ,
следовательно
,
следовательно
![]() =
= .
Теперь в качестве внутреннего интеграла
возьмем интеграл по
.
В области
при произвольном значении
поместим отрезок, параллельный оси
.
Теперь в качестве внутреннего интеграла
возьмем интеграл по
.
В области
при произвольном значении
поместим отрезок, параллельный оси
![]() .
Левая координата отрезка определяется
уравнением
.
Левая координата отрезка определяется
уравнением
![]() ,
а правая координата уравнением
,
а правая координата уравнением
![]() .
Данный отрезок заметает все точки
области
при изменении
.
Данный отрезок заметает все точки
области
при изменении
![]() от 0 до 4. Таким образом,
от 0 до 4. Таким образом,
![]() ,
следовательно
,
следовательно
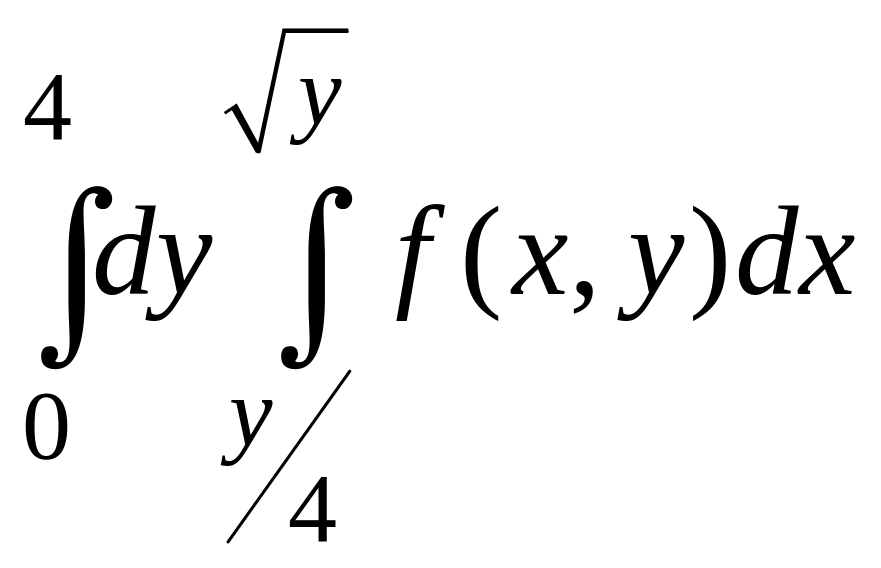 .
.
Пример 4.2. Изменить порядок интегрирования в повторном интеграле
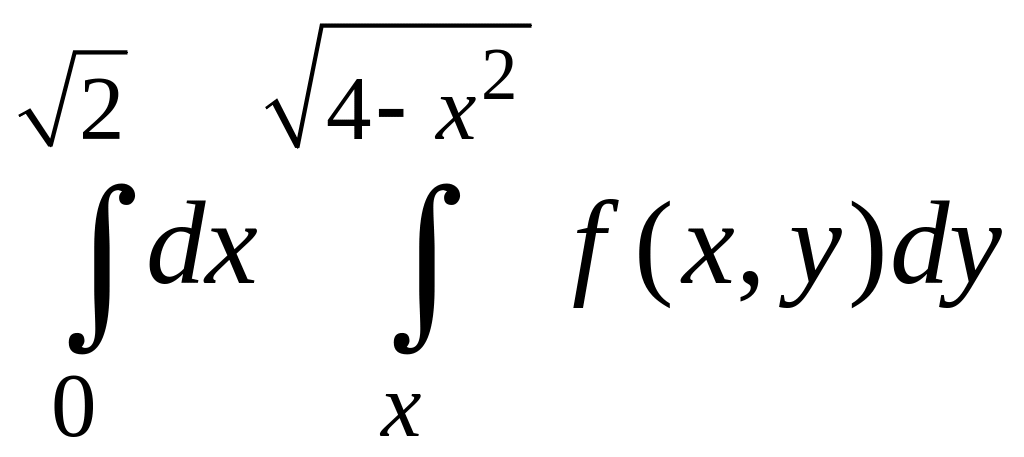 .
.
Решение.
По пределам интегрирования повторного
интеграла определим область интегрирования
.
Так как внутренний интеграл берется по
,
его пределы показывают, какими линиями
ограничена область
снизу и сверху. Пределы внешнего интеграла
показывают, между какими вертикальными
прямыми расположена область
.
Таким образом,
![]() .
Ч
.
Ч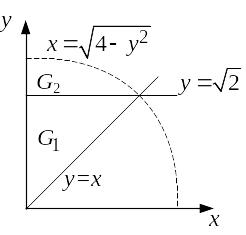 тобы
изменить порядок интегрирования в
повторном интеграле область
при помощи прямой
тобы
изменить порядок интегрирования в
повторном интеграле область
при помощи прямой
![]() разбиваем на две области
разбиваем на две области
![]() и
и
![]() .
.
![]() ,
,
![]() .
Эти области можно представить в виде:
.
Эти области можно представить в виде:
![]() ,
,
![]() .
Следовательно, повторный интеграл буден
иметь вид:
.
Следовательно, повторный интеграл буден
иметь вид:
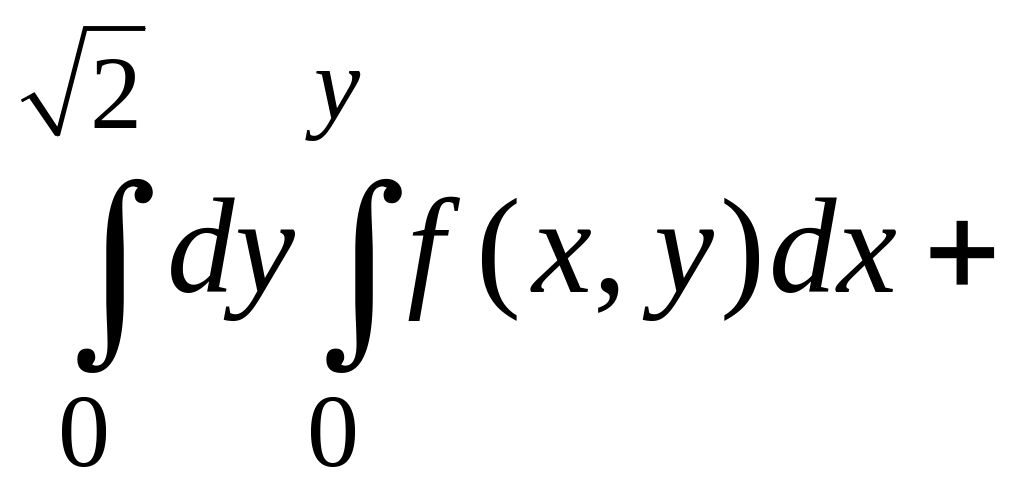
 .
.
Пример 4.3. Расставить различными способами пределы интегрирования в тройном интеграле
![]()
 .
.
Решение.
По пределам интегрирования повторного
интеграла определим область интегрирования
![]() - конус с вершиной в начале координат и
с осью, совпадающей с осью
.
Записав множество
в виде
- конус с вершиной в начале координат и
с осью, совпадающей с осью
.
Записав множество
в виде
![]() ,
получим
,
получим
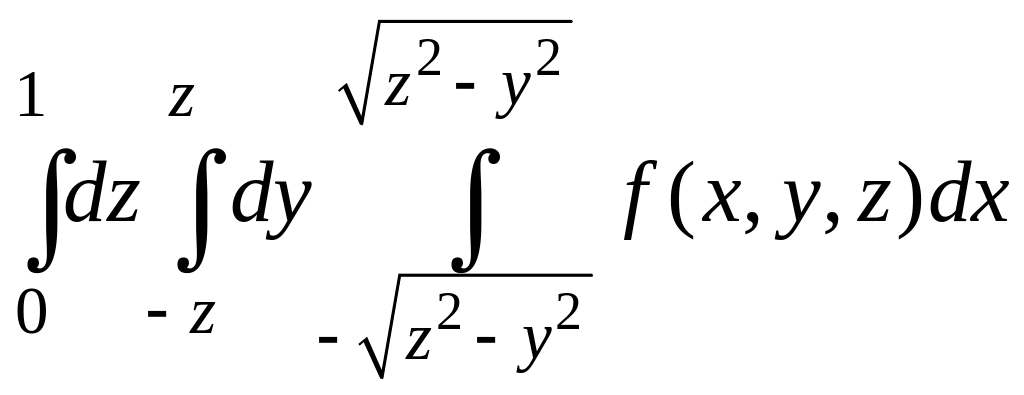 .
Представив
в виде
.
Представив
в виде
![]() ,
получим
,
получим
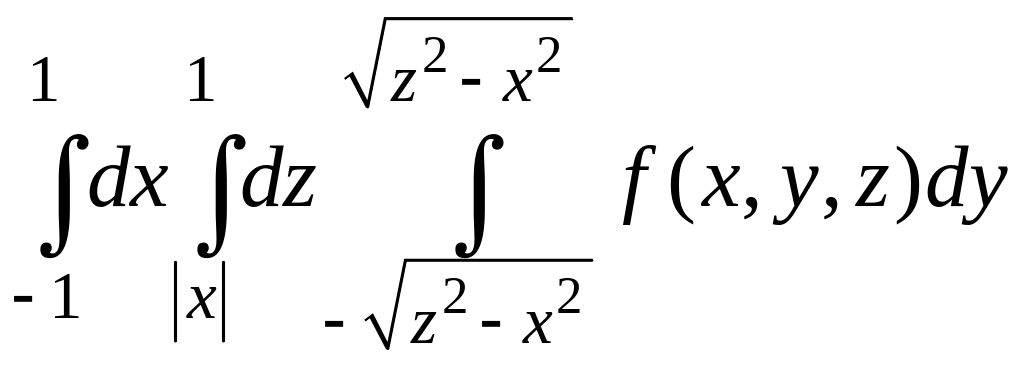 .
.
Пример 4.4. Вычислить
двойной интеграл
 ,
где область интегрирования
задана пересечением прямых
,
где область интегрирования
задана пересечением прямых
![]() ,
,
![]() ,
,
![]() .
.
Решение.
Двойной интеграл сведем к повторному
с внутренним интегралом по
и внешним по
.
Область
представим в виде:
![]() .
Тогда получаем интеграл
.
Тогда получаем интеграл
 .
Проинтегрировать его не представляется
возможным, так как первообразная для
подынтегральной функции внутреннего
интеграла
.
Проинтегрировать его не представляется
возможным, так как первообразная для
подынтегральной функции внутреннего
интеграла
![]() не выражается через элементарные
функции.
не выражается через элементарные
функции.
Поменяем порядок
интегрирования. Для этого область
интегрирования представим в виде:
![]() .
Двойной интеграл сводится к повторному
интегралу следующего вида
.
Двойной интеграл сводится к повторному
интегралу следующего вида
 .
Этот интеграл легко вычисляется
.
Этот интеграл легко вычисляется
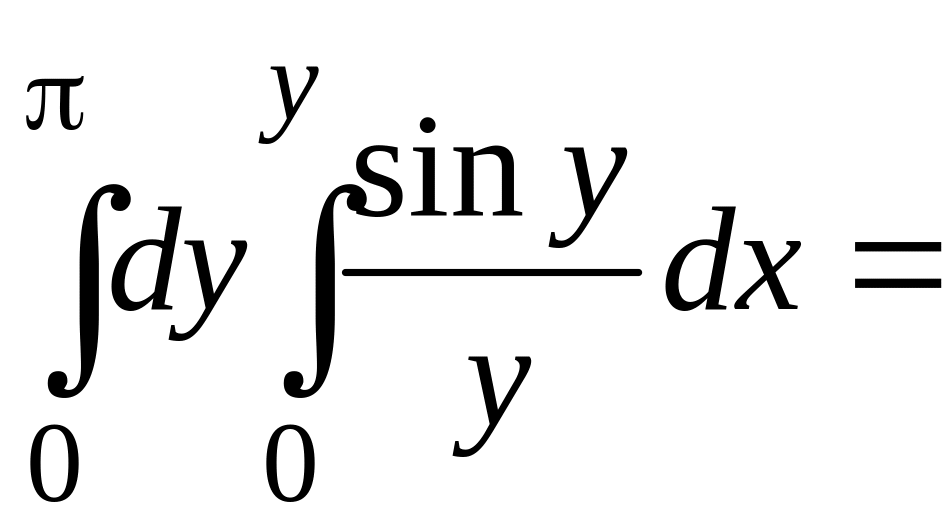
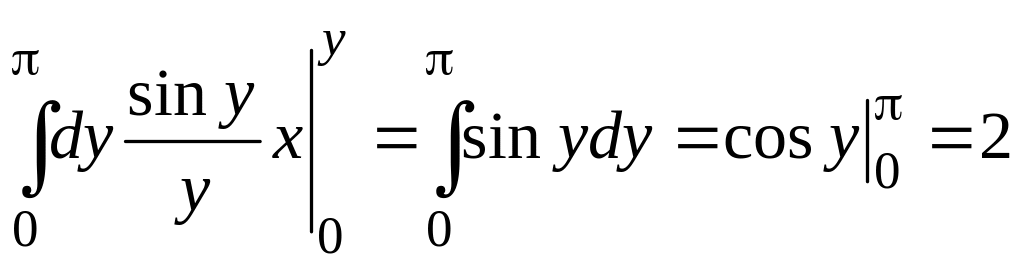 .
.
Пример 4.5. Вычислить
тройной интеграл
![]() ,
где область интегрирования
ограничена поверхностями
,
где область интегрирования
ограничена поверхностями
![]() ,
,
,
,
![]() и координатной плоскостью
и координатной плоскостью
![]() .
.
Решение.
Множество
снизу ограничено плоской поверхностью
сверху некоторой поверхностью
и с боков цилиндрическими поверхностями
,
.
Это позволяет свести наш тройной интеграл
к двойному по проекции множества
на плоскость
и к однократному по
![]() :
:
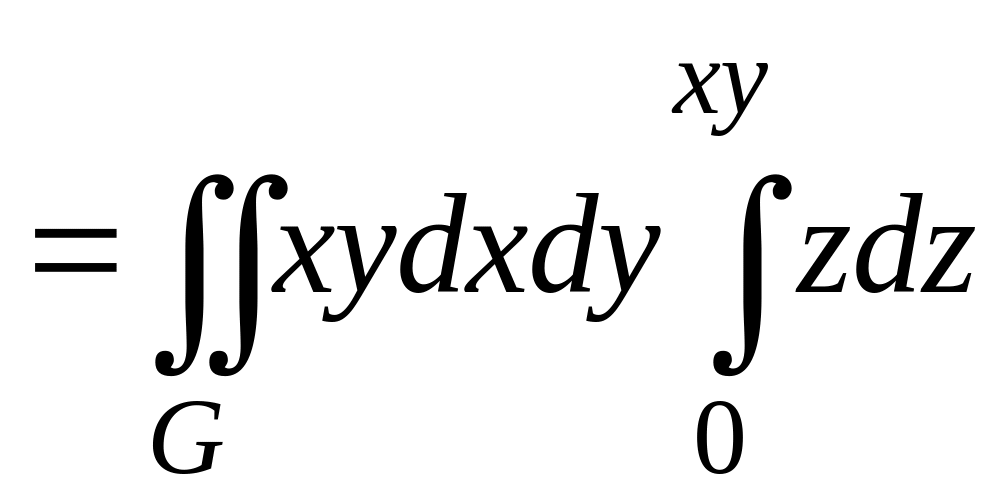 .
Вычисляя однократный интеграл, получаем
.
Вычисляя однократный интеграл, получаем
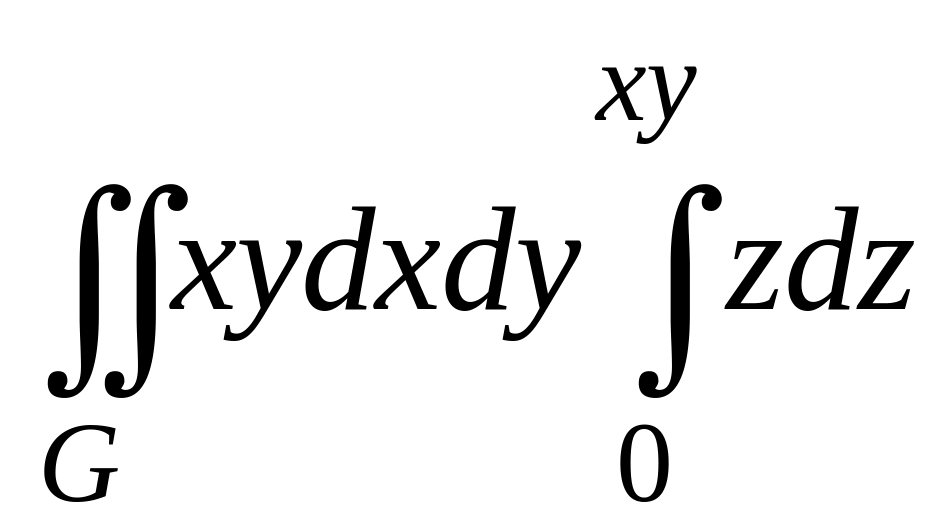
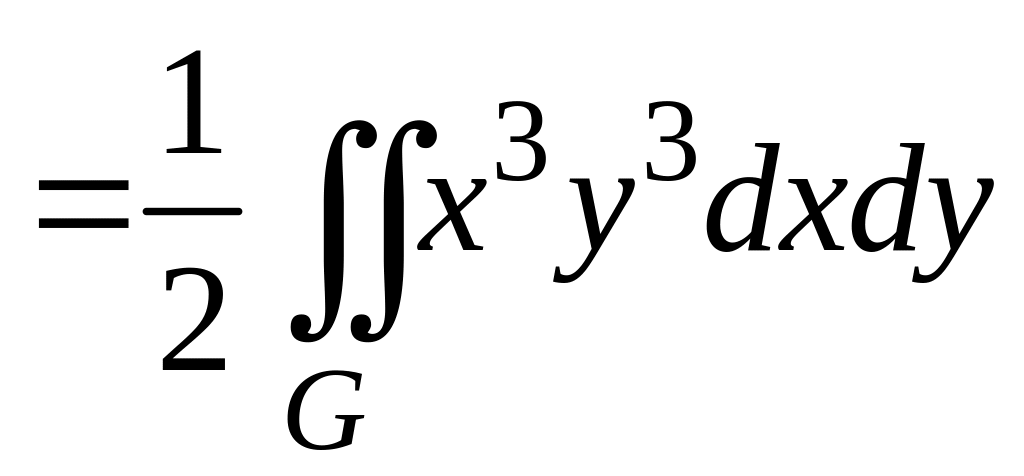 .
Для вычисления полученного двойного
интеграла изобразим область
.
Кривые
и
пересекаются в точках
и
.
Для вычисления полученного двойного
интеграла изобразим область
.
Кривые
и
пересекаются в точках
и
![]() .
Внутри области
при произвольном
помещаем отрезок, параллельный оси
.
Концы отрезка лежат на кривых
и
,
поэтому координаты концов
.
Внутри области
при произвольном
помещаем отрезок, параллельный оси
.
Концы отрезка лежат на кривых
и
,
поэтому координаты концов
![]() и
и
![]() .
При перемещении отрезка параллельно
оси
от точки 0 до точки 1 он заметает все
точки множества
.
Таким образом, множество
записывается в виде
.
При перемещении отрезка параллельно
оси
от точки 0 до точки 1 он заметает все
точки множества
.
Таким образом, множество
записывается в виде
![]() ,
следовательно, наш двойной интеграл
сводится к повторному
,
следовательно, наш двойной интеграл
сводится к повторному

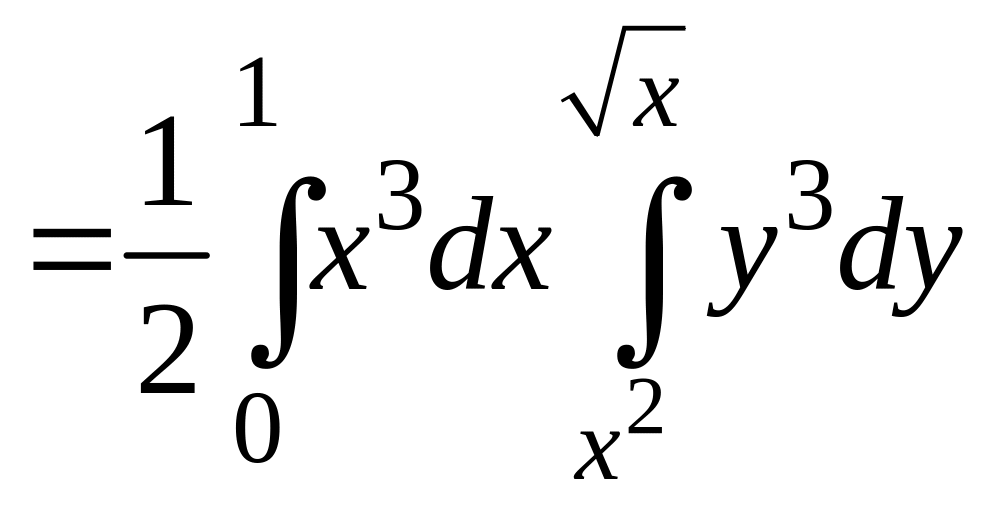 .
Вычисляем повторный интеграл
.
Вычисляем повторный интеграл
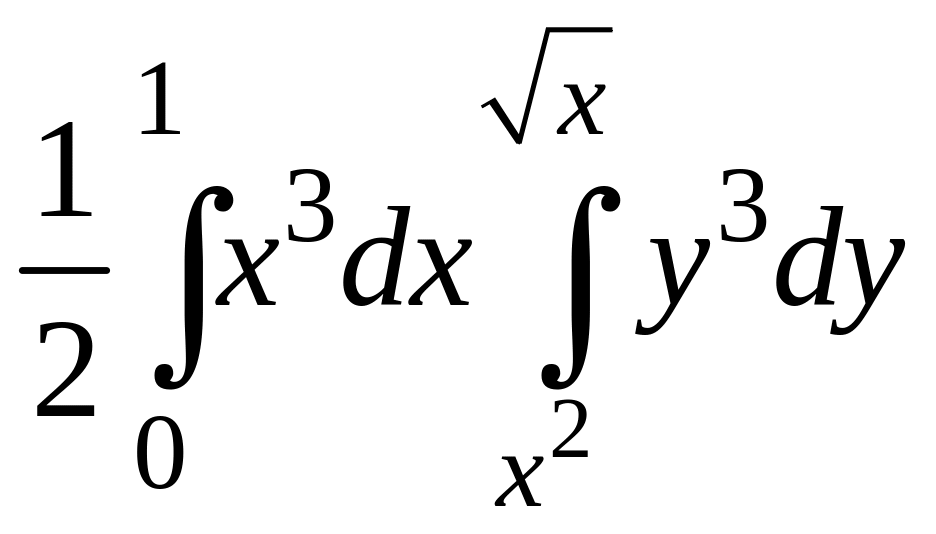
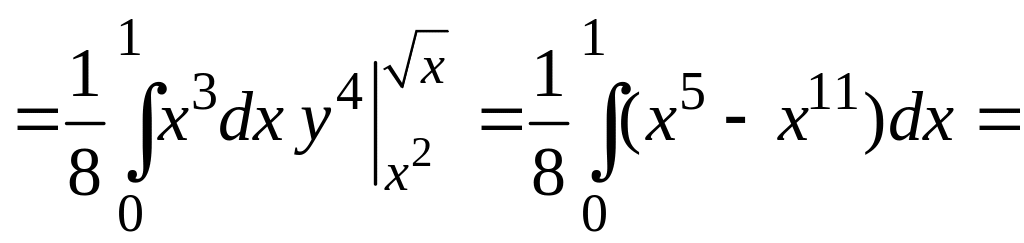
![]() .
.
П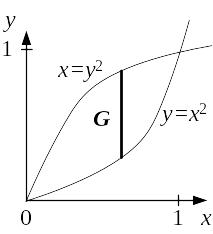 ример
4.6. Вычислить
тройной интеграл
ример
4.6. Вычислить
тройной интеграл
![]() ,
где область интегрирования
ограничена координатными плоскостями
,
,
где область интегрирования
ограничена координатными плоскостями
,
![]() ,
и плоскостью
,
и плоскостью
![]() .
.
Р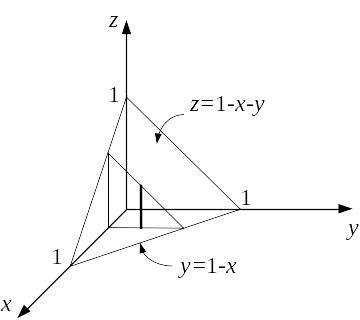 ешение.
Тройной интеграл сведем к повторному
с внутренним интегралом по
.
Для этого внутри области
при произвольных
и
поместим отрезок, параллельный оси
.
Нижняя координата этого отрезка равна
0, а верхняя координата равна
ешение.
Тройной интеграл сведем к повторному
с внутренним интегралом по
.
Для этого внутри области
при произвольных
и
поместим отрезок, параллельный оси
.
Нижняя координата этого отрезка равна
0, а верхняя координата равна
![]() .
Перемещая отрезок параллельно оси
от
до
.
Перемещая отрезок параллельно оси
от
до
![]() ,
получаем все точки плоской поверхности
расположенной в области
при произвольном
.
Перемещение полученной плоской
поверхности параллельно оси
от
до
,
получаем все точки плоской поверхности
расположенной в области
при произвольном
.
Перемещение полученной плоской
поверхности параллельно оси
от
до
![]() заметает все точки области
.
Таким образом область
записывается в виде:
заметает все точки области
.
Таким образом область
записывается в виде:
![]() ,
следовательно
,
следовательно
![]()
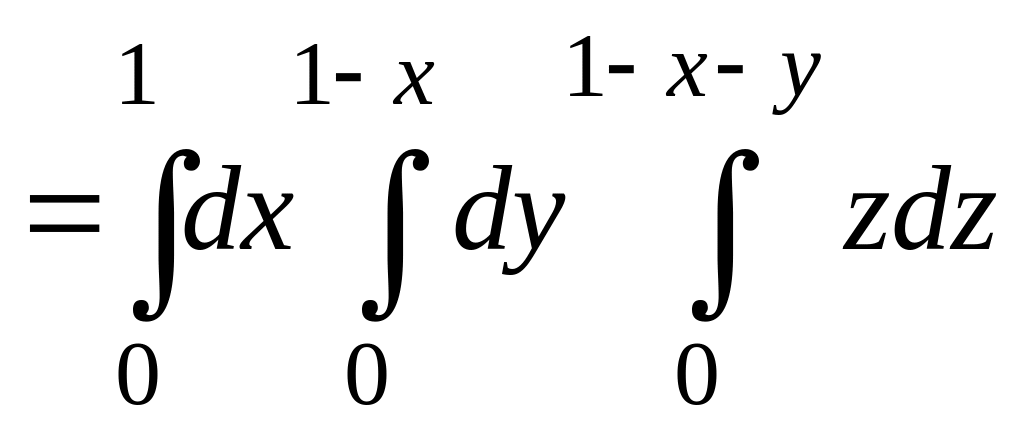
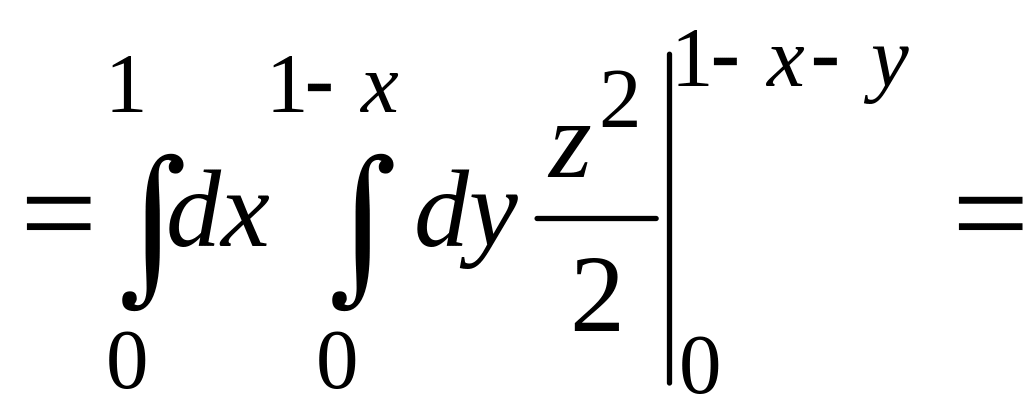
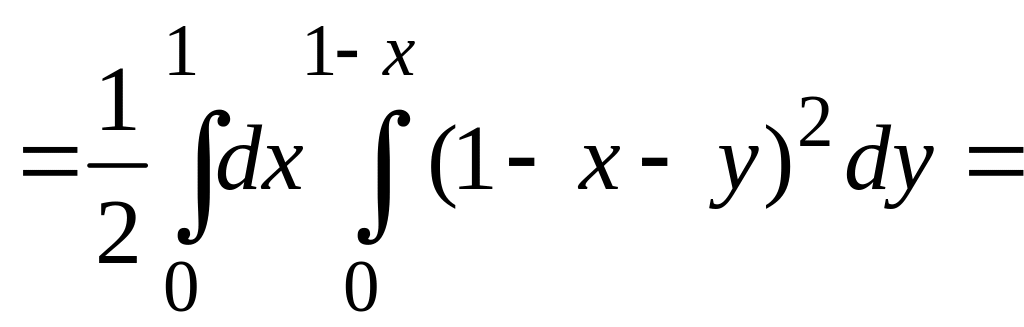
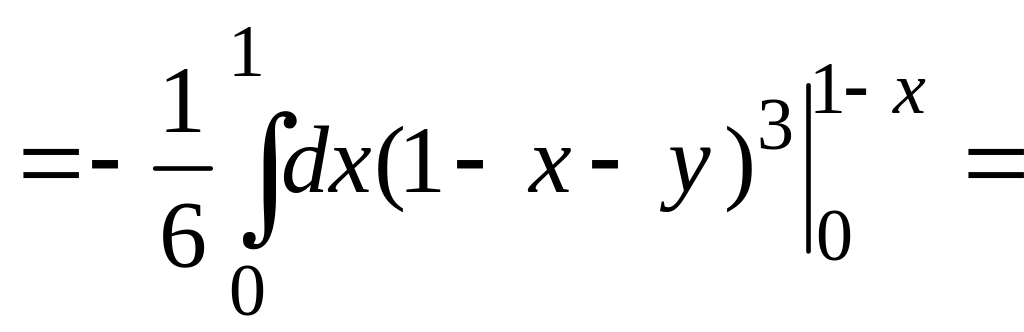
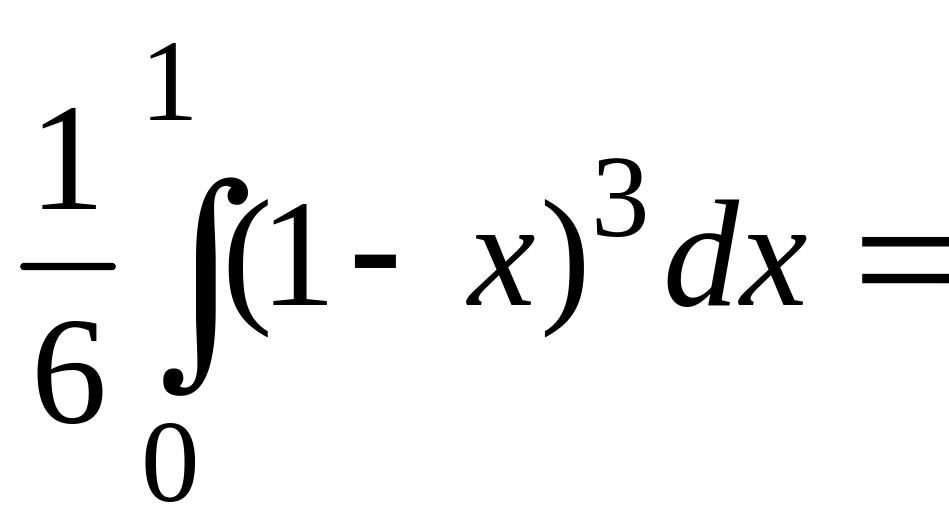
![]() .
.
