• Спектральный анализ — обработка речевых, звуковых, сейсмических, гидроакустических сигналов; распознавание образов

• Частотно-временной анализ — компрессия изображений, гидро- и радиолокация, разнообразные задачи обнаружения сигнала

• Адаптивная фильтрация — обработка речи, изображений, распознавание образов, подавление шумов, адаптивные антенные решетки

• Нелинейная обработка — вычисление корреляций, медианная фильтрация; синтез амплитудных, фазовых, частотных детекторов, обработка речи, векторное кодирование

• Многоскоростная обработка — интерполяция (увеличение) и децимация (уменьшение) частоты дискретизации в многоскоростных системах телекоммуникации, аудиосистемах

• Свертка - традиционные типы

• Секционная свертка

• 1. Дискретизация полосовых сигналов

Выполнить дискретизацию радиосигнала S(t) методом полосовой дискретизации.

N=84

B=1 (номер по журналу)

Дано:

f_с=N(группы) – частота сигнала , f_с=84 МГц;

B=12 МГц – полоса частот радиосигнала.

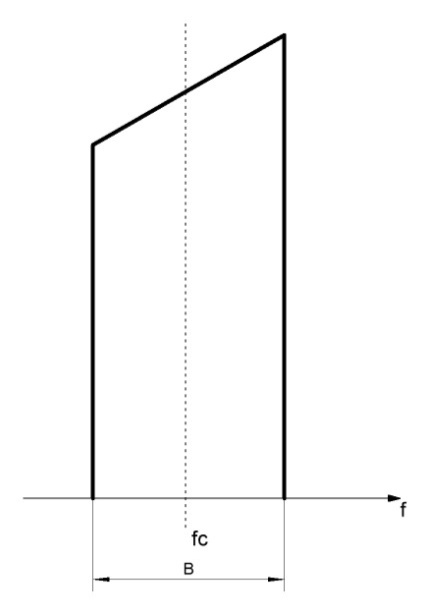
Рисунок 1.1 – Полосовой радиосигнал.

Решение:

Определить диапазон целочисленных значений коэффициента k.

f₁= f_с- B/2= 84-12/2=78МГц (нижняя частота сигнала)

f₂= f_с+B/2= 84+12/2=90 МГц (верхняя частота сигнала)

k выбираем исходя из условия:

k<f₁/(f₂-f₁)=78/(90-78)=6,5. Округляем до целого в меньшую сторону.

K=6

Определить диапазон возможных частот дискретизации .

Диапазон дискретизации выбираем из условия :

(2f_с +B)/(k+1)≤f_d≤(2f_с -B)/k (*)

При k=1: (2*84+12)/2 ≤f_d≤(2*84-12)/1; 90≤f_d≤156

При k=2: (2*84+12)/3 ≤f_d≤(2*84-12)/2; 60≤f_d≤78

При k=3: (2*84+12)/4 ≤f_d≤(2*84-12)/3; 45≤f_d≤52

При k=4: (2*84+12)/5 ≤f_d≤(2*84-12)/4; 36≤f_d≤39

При k=5: (2*84+12)/6 ≤f_d≤(2*84-12)/5; 30≤f_d≤31,2

При k=6: (2*84+12)/7 ≤f_d≤(2*84-12)/6; 25,71≤f_d≤26

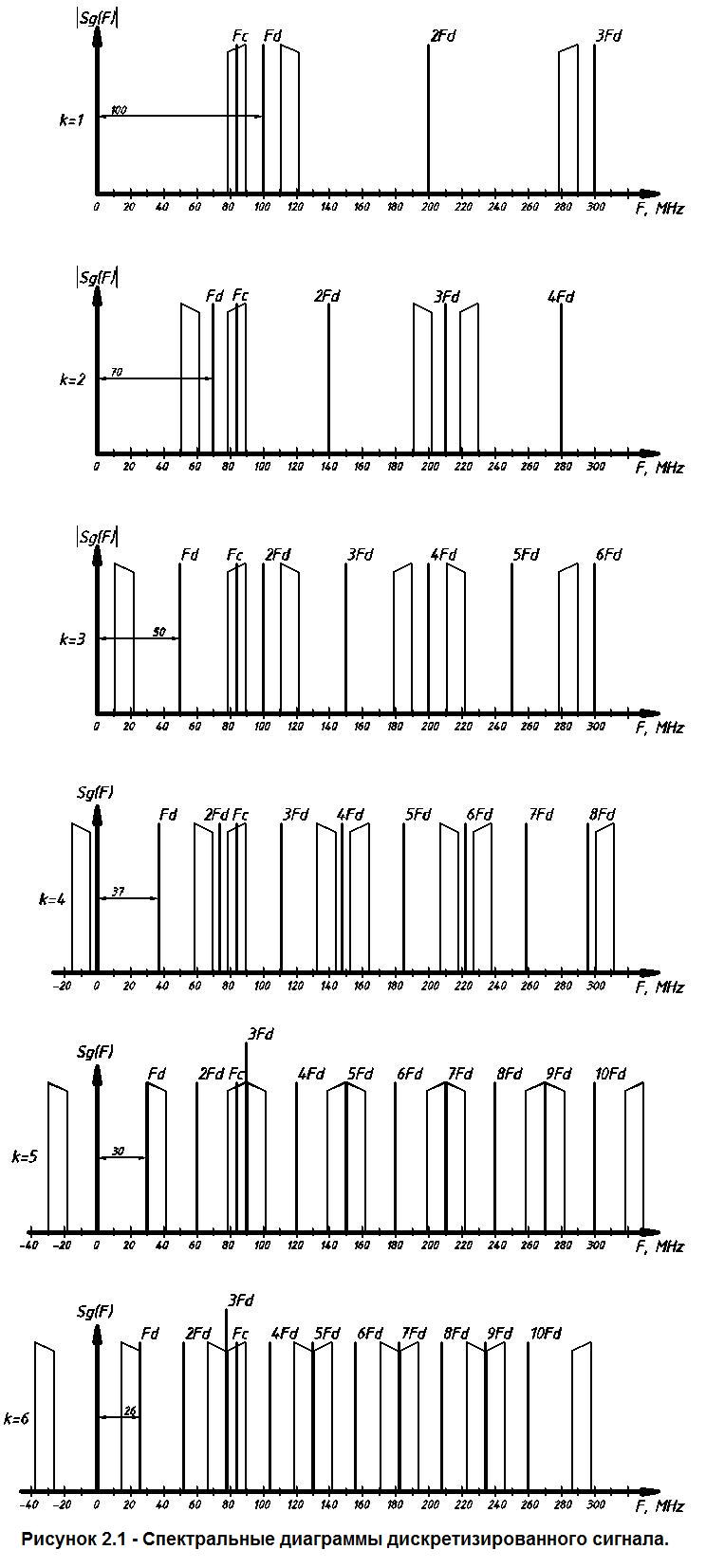
Построить спектральные диаграммы дискретизированного сигнала для полученных значений k и частот дискретизации. Обозначить на спектре положительные частоты дискретизации и пронумеровать соответствующие полосы дискретизации для всех k.

{Значение f_d для каждого k ,берём любое исходя из интервала!}

См. рисунок 1.2

Полосовой сигнал это тот сигнал, центральная частота которого не равна нулю.

Важно чтобы не было наложения сигнала. Для точного восстановления сигнала по его дискретным отчетам требуется обеспечить отсутствие перекрытий сдвинутых копий спектра. При этом восстановление исходного сигнала происходит при помощи цифрового фильтра.

При некотором целом значении k зеркальная половина спектра должна быть распооложена между k и k+1 сдвинутыми копиями спектра из условия (*).

2. Исследование дпф и одпф

2.1

• Вычислить ДПФ периодического сигнала S(t). Построить комплексный спектр ПФ, спектр ДПФ.

• На спектре ДПФ указать соответствующие отчеты спектра и соответствующие частоты в Гц.

• Отчеты сигнала берутся в соответствии с условием: ;

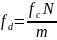• Привести временную диаграмму отчетов сигнала на 2 периодах и диаграмму ДПФ.

Дискретное преобразование Фурье (в англоязычной литературе DFT, DiscreteFourierTransform) — это одно из преобразований Фурье, широко применяемых в алгоритмах цифровой обработки сигналов (его модификации применяются в сжатии звука в MP3, сжатии изображений в JPEG и др.), а также в других областях, связанных с анализом частот в дискретном (к примеру, оцифрованном аналоговом) сигнале. Дискретное преобразование Фурье требует в качестве входа дискретную функцию. Такие функции часто создаются путём дискретизации (выборки значений из непрерывных функций). Дискретные преобразования Фурье помогают решать частные дифференциальные уравнения и выполнять такие операции, как свёртки. Дискретные преобразования Фурье также активно используются в статистике, при анализе временных рядов. Преобразования бывают одномерные, двумерные и даже трёхмерные.

Решение:

№_группы=84; №_{по журналу}=1;

N – количество точек ДПФ и количество сигнала на 2 периодах.

N=8;

f_c= частота сигнала S(t).

f_c=№_группы+№_{по журналу}=84+1=85 Гц

S(t)=cos(2πf_ct);

m=1;

S(t), N, m - у всех одинаковый!

f_d= частота дискретизации

f_d=85*8/1=680 Гц

U_m=1

С_n= ;

С_n= коэфф. ряда Фурье.

|С_n|= |С_-n|= U_m/2=0.5

Строим комплексный спектр ПФ.

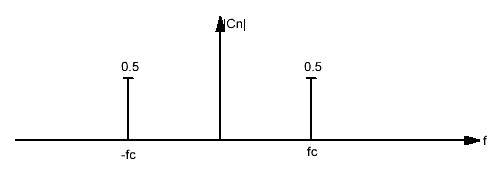
Рисунок 2.1.1Комплексный спектр ПФ входного сигнала.

Сигнал S(t):

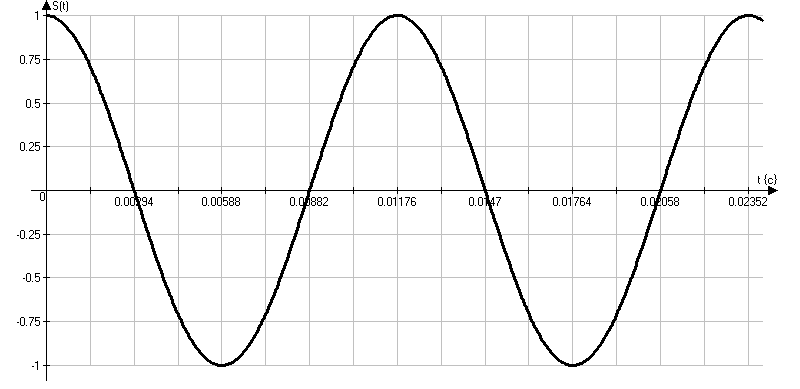
Рисунок 2.1.2. Временная диаграмма входного сигнала.

Разбили на N отчетов за период.

Δt=1/f_d – интервал дискретизации.

Δt=1/680=1.47*10^-3c

T – период сигнала.

T=1/f_c=11.76*10^-3c

Проверим: N=T/ Δt= 11.76*10^-3c/1.47*10^-3c=8

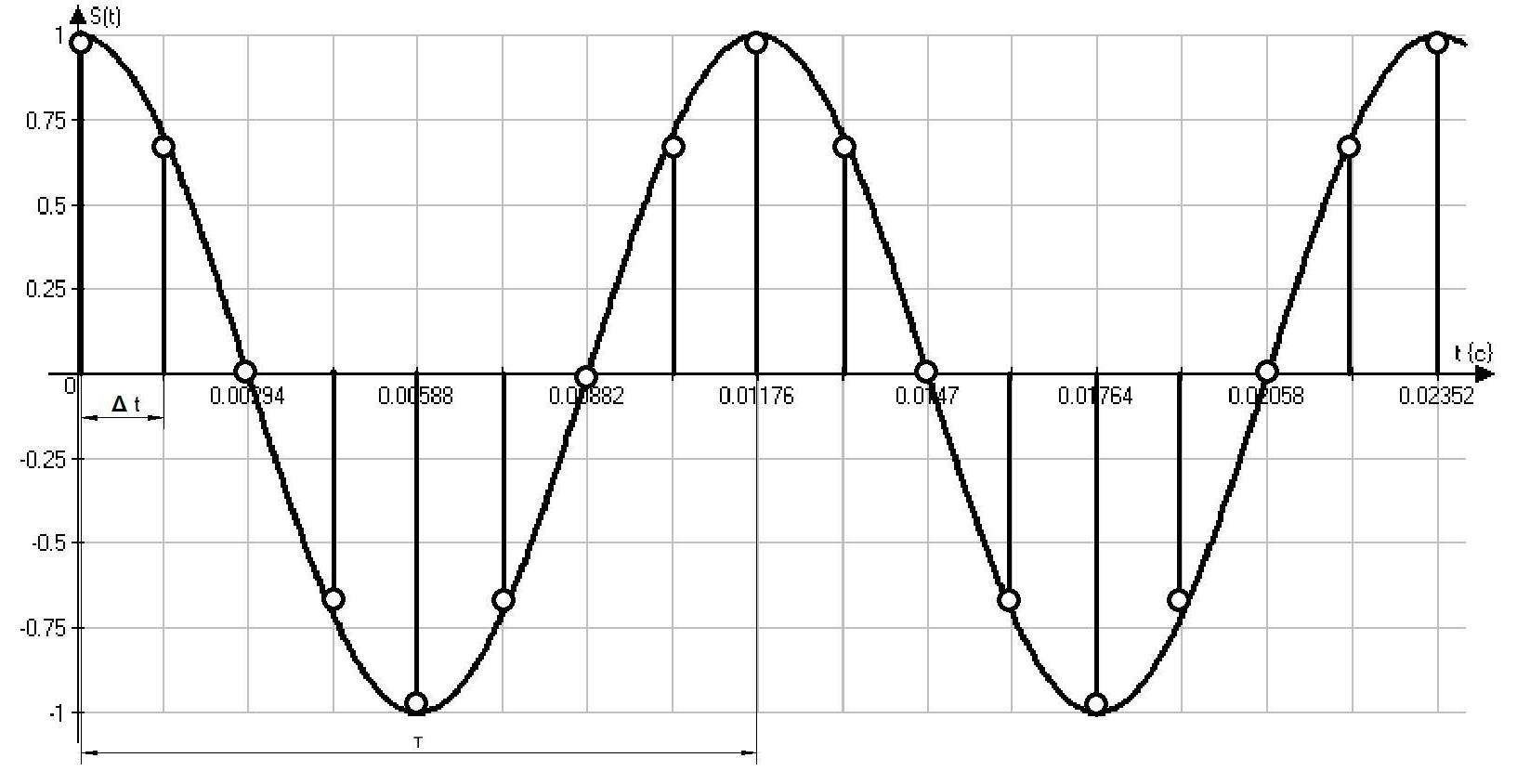
Рисунок 2.1.3. Временная диаграмма отчетов и входного сигнала на 2ух периодах.

Вычисление ДПФ (*):

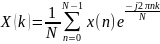
Отчеты за период находим исходя из:

x(n)=cos(2π85*nΔt), n=0 N-1

n=0…7

x(n)={1; 0,707; 0; -0.707; -1; -0.707; 0; 0.707}

x(k)=1/8 * (1e^-j2πk0/8+0.707e^-j2πk1/8+0e^-j2πk2/8 - 0.707e^-j2πk3/8-1e^-j2πk4/8-0.707e^-j2πk5/8+

+0e^-j2πk6/8+0.707e^-j2πk7/8)

ИспользуемформулуЭйлера: e^ja=cos(a) + j sin(a)

k=0;

x(0)=(1+0.707+0-0.707-1-0.707+0+0.707)/8=0

k=1;

x(1)= 1/8 * (1+0.707e^-jπ/4 - 0.707e^-j3π/4-e^-jπ-0.707e^-j5π/4+0.707e^-j7π/4)=

(1+0.707(-0.707-0.707j)-0.707(-0.707-0.707j)-1(-1+0)-0.707(-0.707+0.707j)+

+0.707(0.707+0.707j)/8=(1+0.5-0.5j+0.5+0.5j+1+0.5-0.5j+0.5+0.5j)/8=0.5;

k=2

x(2)= 1/8 * (1+0.707e^-jπ/2 - 0.707e^-j3π/2-e^-j2π-0.707e^-j5π/2+0.707e^-j7π/2)=

=(1+0.707(0-1j)-0.707(0+1j)-1(1-0)-0.707(0-j) +0.707(0+j))/8=

=(1-0.707j-0.707j-1+0.707j+0.707j)=0;

k=3

x(3)= 1/8 * (1+0.707e^-j3π/4 - 0.707e^-j9π/4-e^-j3π-0.707e^-j15π/4+0.707e^-j21π/4)=

=(1+0.707(-0.707-0.707j)-0.707(0.707-0.707j)-1(-1+0)-0.707(0.707+0.707j)+

+0.707(-0.707+0.707j)/8=(1-0.5-0.5j-0.5+0.5j+1-0.5j+0.5j-0.5)/8=0;

k=4

x(4)= 1/8 * (1+0.707e^-jπ- 0.707e^-j3π-e^-j4π-0.707e^-j5π+0.707e^-j7π)=

=(1+0.707(-1+0)-0.707(-1+0)-1(1-0)-0.707(-1+0)+0.707(-1+0))/8=

(1-0.707+0.707-1+0.707-0.707)/8=0;

k=5

x(5)= 1/8 * (1+0.707e^-j5π/4 - 0.707e^-j15π/4-e^-j5π-0.707e^-j25π/4+0.707e^-j35π/4)=

=(1+0.707(-0.707+0.707j)-0.707(0.707+0.707j)-1(-1+0)-0.707(0.707-0.707j)+

+0.707(-0.707-0.707j))/8=1-0.5+0.5j-0.5-0.5j+1-0.5+0.5j-0.5-0.5j=0;

k=6

x(6)= 1/8 * (1+0.707e^-j3π/2 - 0.707e^-j9π/2-e^-j6π-0.707e^-j15π/2+0.707e^-j21π/2)=

=(1+0.707(0+1j)-0.707(0-1j)-1(1+0)-0.707(0+1j)+0.707(0-1j))/8=

=(1+0.707+0.707-1-0.707-0.707)/8=0;

K=7

x(7)= 1/8 * (1+0.707e^-j7π/4 - 0.707e^-j21π/4-e^-j7π-0.707e^-j35π/4+0.707e^-j49π/4)=

1+0.707(-0.707-0.707j)-0.707(-0.707-0.707j)-1(-1+0)- 0.707(-0.707+0.707j)+

+0.707(0.707+0.707j)/8=(1+0.5-0.5j+0.5+0.5j+1+0.5-0.5j+0.5+0.5j)/8=0.5

Модуль (фаза) спектра:

x(0)=0 (0⁰)

x(1)=0.5 (0⁰)

x(2)=0 (0⁰)

x(3)=0 (0⁰)

x(4)=0 (0⁰) => симметрия относительно N/2= 4

x(5)= 0 (0⁰)

x(6)= 0 (0⁰)

x(7)=0,5 (0⁰)

….x(8) =0 (0⁰)(значения повторяются)

Отчеты сигнала, модуль спектра и фазовый спектр строим в MatLab (отчеты начинаются от единички!):

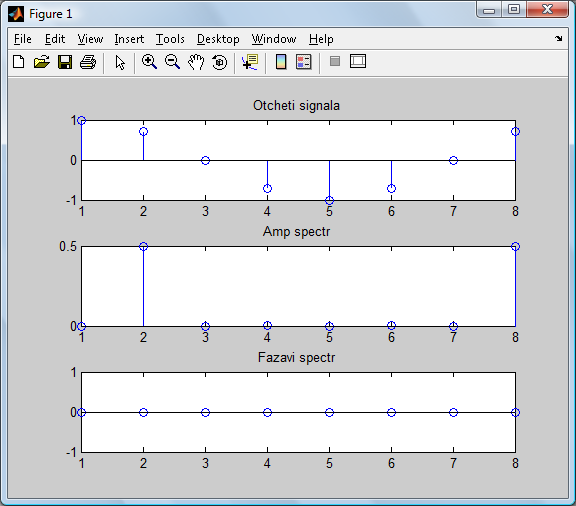
Рисунок 2.1.4. Отчеты сигнала, и диаграммы ДПФ.

2.2

• Произвести дискретизацию сигнала в соответствии с условием:

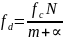
• Вычислить ДПФ отрезка сигнала при данных условиях дискретизации.

• Привести временную диаграмму отчетов сигнала на двух периодах и диаграмму ДПФ. Сравнить спектр с результатом 1 задачи.

Решение:

α – по табличке.

α=0,4

f_d=85*8/(1+0,4) ≈486 Гц

Δt₂=1/f_d – интервал дискретизации.

Δt₂=1/486=2,05*10^-3c

T – период сигнала.

T=1/f_c=11.76*10^-3c

Столько интервалов дискретизации Δt₂ укладывается на один период T:

N2=T/ Δt₂= 11.76*10^-3c/2,05*10^-3c=5,71

Тогда число отчетов на первый период N₂=6

Временная диаграмма и отчеты на двух периодах

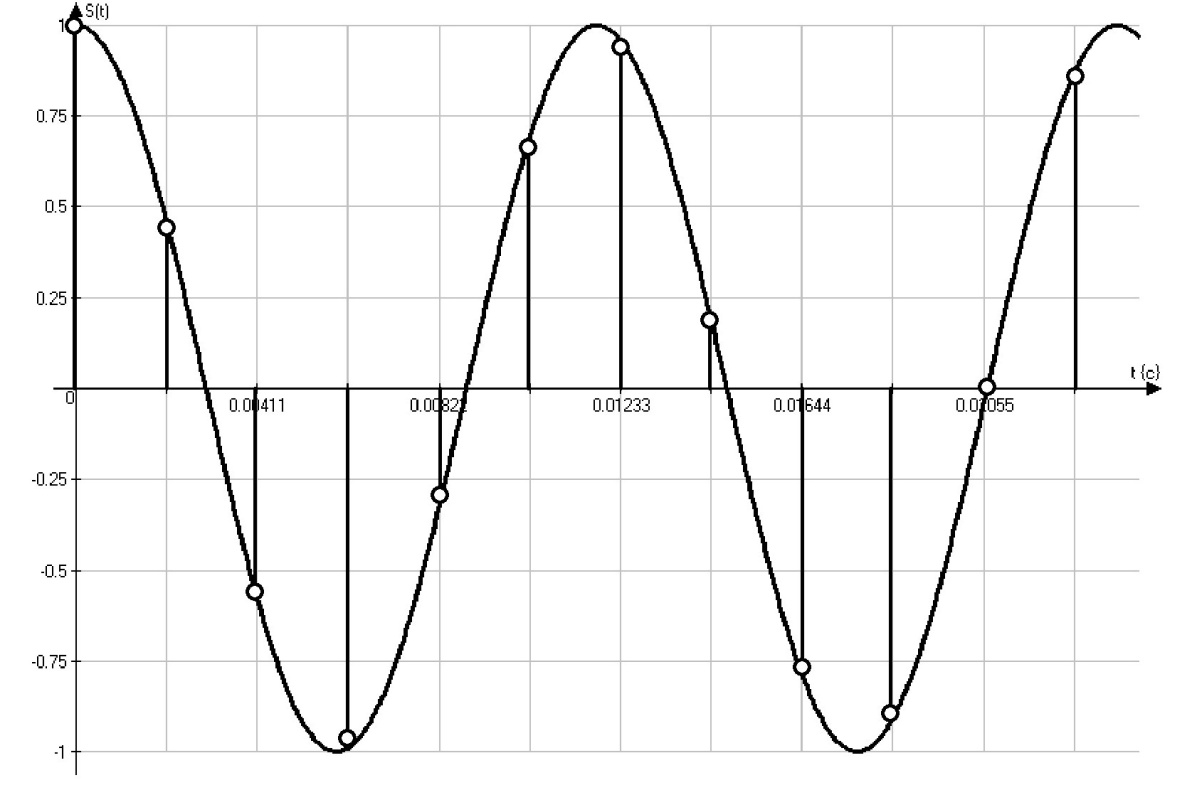
Рисунок 2.2.1Временная диаграмма отчетов и входного сигнала на 2ух периодах

Вычисляем ДПФ как и в (*) используя MatLab.

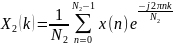
Отчеты за первый период находим исходя из:

x(n)=cos(2π85*nΔt₂), n=0 N-1

n=0…5

x₂(n)={1; 0.454; -0.588; -0.988; -0.309; 0.707}

Отчеты сигнала, модуль спектра и фазовый спектр строим в MatLab (отчеты начинаются от единички!):

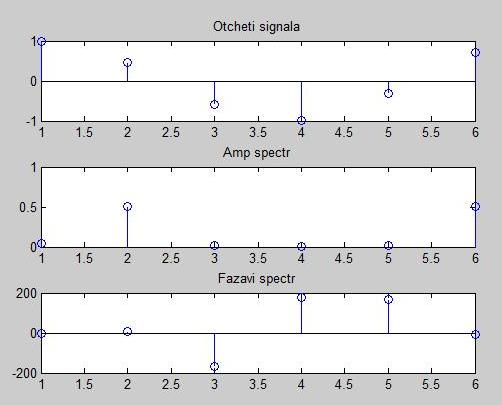
Рисунок 2.1.2Отчеты сигнала, и диаграммы ДПФ.

X₂(n)={0.2766+0j; 3.0166+0.4606j; -0.1198-0.0222j; -0.0702+0j; -0.1198+0.0222j;3.0166-0.4606j)

Сравнивая спектр ДПФ периодических и непериодических (реальных) отчетов, видим, что спектр ДПФ расширяется (растекается). т.е энергия перераспределяется.

2.3

• Для дискретных отчетов сигнала из первой части вычислить ДПФ с применением взвевающих оконных функций

Решение:

По табличке: окно Блэкмана.

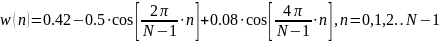
Вычисляем ДПФ, используя MatLab.Отчеты за первый период находим исходя из:

x(k)=x₂(n)*w(n);

x(k)={0; 0.068; -0.286; -0.997; -0.37; 0.05; 0}

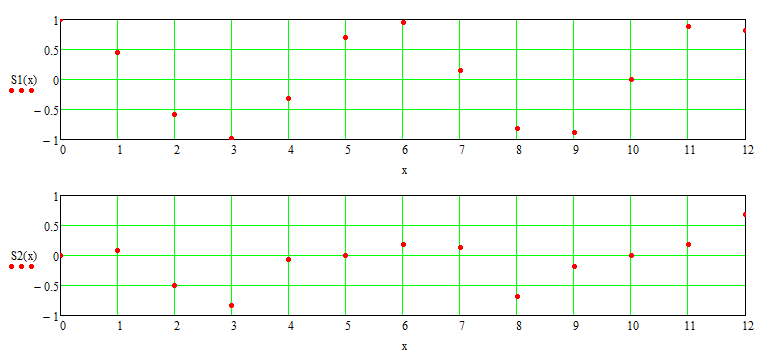
Рисунок 2.3.1 Отчёты сигналов, полученных в MathCad'e

где S(x) – отчёты сигнала при дискритизацииcos(2π85*n Δt₂) ,

S2(x) - отчёты сигнала при не периодичном выборе Δt₂

с домножением на окно Блэкмена.

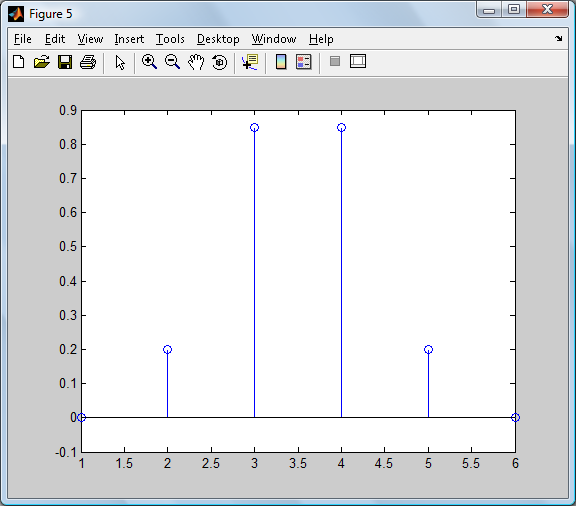
Рисунок 2.3.2. Функция окна. (Блэкмена.)

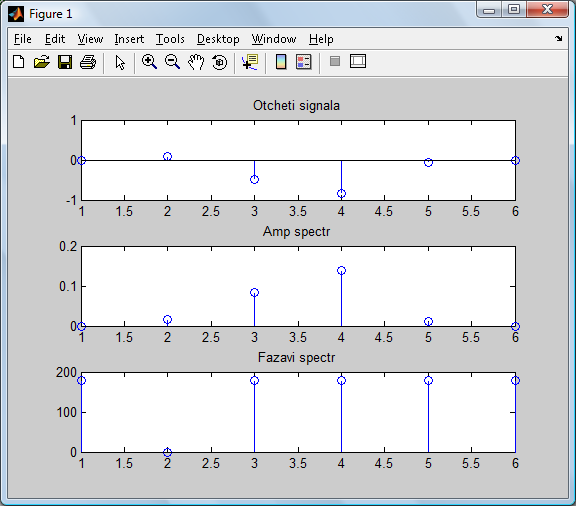
Рисунок 2.3.3Отчеты сигнала, и диаграммы ДПФ.

X(k)={-1.308+0i; 1.165+0.29996j; -0.6037-0.4575j; 0.1864+0j; -0.6037+0.4576j; 1.165-0.2996j}

Для того чтобы уменьшить явление растекания спектра необходимо правильно выделить окно w(n). Для снижения эффекта размывания спектра применяют соответствующие оконные функции. Сравнивая спектр ДПФ из пункта 2 и полученный спектр ДПФиз пункта 3, видим, что фильтрация сигнала, значительно исказит отчёты. Для того, чтобы уменьшить степень искажений (и тем самым упростить фильтр) необходимо применение других взвешенных окон.

2.4

• Вычистить ОДПФ сигнала по отчетам ДПФ с рядом Фурье. Изобразить временную функцию на длительности двух периодов.

Решение:

X(k)={-1.308+0i; 1.165+0.29996j; -0.6037-0.4575j; 0.1864+0j; -0.6037+0.4576j; 1.165-0.2996j}

Используя формулу для вычисления Обратного преобразования Фурье,:

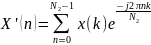
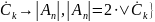, в нашем случае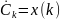

Аппроксимируем сигнал тригонометрической формой ряда Фурье:

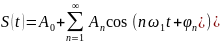
, где

ω₁=2πfc

n 0 до 5

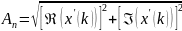
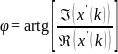
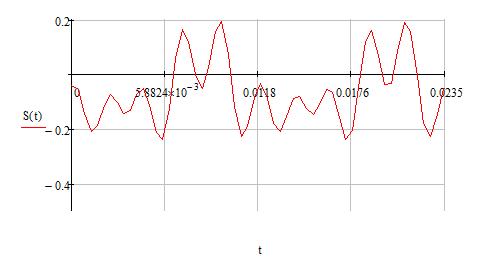
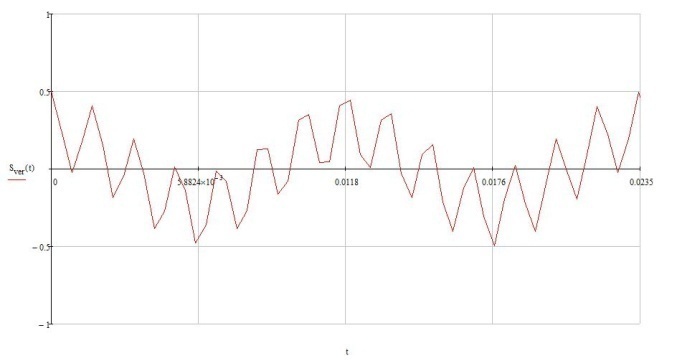
а б

Рисунок 4.1. Временные диаграммы на 2х периодах, полученные после прохождения через ФНЧ сигналов

а) с растеканием спектра (апериодичнойf_d).

б) с периодичной дискритизацией.

Для того, чтобы переданный и передаваемый сигнал имел большую схожесть, необходимо: во-первых, правильно выбрать частоту дискритизации; во-вторых, правильно выбрать взвешанное окно; в-третьих, аппроксимировать сигнал фильтром высокого порядка.

3. Проектирование цифрового фильтра (ЦФ)

Проектирование ЦФ со строго линейной ФЧХ

1. По заданному варианту выполнить проектирование ЦФ в среде Matlab. Применить два метода - метод весовых окон и метод частотной выборки. Выполнить предварительный расчет по оценке

порядка фильтра.

2. Привести результаты проектирования в виде графиков ИР, АЧХ и ФЧХ при условии невыполнения требований к фильтру и при выполнении требований. Порядок фильтра выбирается минимально необходимым для снижений вычислительной сложности при реализации.

3. Привести текст программы расчета фильтра с комментариями

Цифровой фильтр — в электронике любой фильтр, обрабатывающий цифровой сигнал с целью выделения и/или подавления определённых частот этого сигнала. В отличие от цифрового аналоговый фильтр имеет дело с аналоговым сигналом, его свойства недискретны, соответственно передаточная функция зависит от внутренних свойств составляющих его элементов.

Применения.

Цифровые фильтры на сегодняшний день применяются практически везде, где требуется обработка сигналов, в частности в спектральном анализе, обработке изображений, обработке видео, обработке речи и звука и многих других приложениях.

Характеристика цифровых фильтров

Линейный стационарный цифровой фильтр характеризуется передаточной функцией. Передаточная функция может описать, как фильтр будет реагировать на входной сигнал. Таким образом, проектирование фильтра состоит из постановки задачи (например, фильтр восьмого порядка, фильтр низких частот с конкретной частотой среза), а затем производится расчет передаточной функции, которая определяет характеристики фильтра .

Передаточная функция фильтра имеет вид:

где порядок фильтра - большее N или M. В данном случае это формула БИХ-фильтра. Если знаменатель равен единице, то получаем формулу КИХ-фильтра (без обратной связи).

Преимущества и недостатки

Преимуществами цифровых фильтров перед аналоговыми являются:

1. Высокая точность (точность аналоговых фильтров ограничена допусками на элементы).

2. В отличие от аналогового фильтра передаточная функция не зависит от дрейфа характеристик элементов.

3. Гибкость настройки, лёгкость изменения.

4. компактность — аналоговый фильтр на очень низкую частоту (доли герца, например) потребовал бы чрезвычайно громоздких конденсаторов или индуктивностей.

Недостатки

1. Недостатками цифровых фильтров по сравнению с аналоговыми являются:

2. Трудность работы с высокочастотными сигналами. Полоса частот ограничена частотой Найквиста, равной половине частоты дискретизации сигнала. Поэтому для высокочастотных сигналов применяют аналоговые фильтры, либо, если на высоких частотах нет полезного сигнала, сначала подавляют высокочастотные составляющие с помощью аналогового фильтра, затем обрабатывают сигнал цифровым фильтром.

3. Трудность работы в реальном времени — вычисления должны быть завершены в течение периода дискретизации.

4. Для большой точности и высокой скорости обработки сигналов требуется не только мощный процессор, но и дополнительное, возможно дорогостоящее, аппаратное обеспечение в виде высокоточных и быстрых ЦАП и АЦП.

Виды цифровых фильтров

1. КИХ-фильтры

Фильтр с конечной импульсной характеристикой (нерекурсивный фильтр, КИХ-фильтр) — один из видов электронных фильтров, характерной особенностью которого является ограниченность по времени его импульсной характеристики (с какого-то момента времени она становится точно равной нулю). Такой фильтр называют ещё нерекурсивным из-за отсутствия обратной связи. Знаменатель передаточной функции такого фильтра — некая константа.

2. БИХ-фильтры

Фильтр с бесконечной импульсной характеристикой (рекурсивный фильтр, БИХ-фильтр) — электронный фильтр, использующий один или более своих выходов в качестве входа, то есть образует обратную связь. Основным свойством таких фильтров является то, что их импульсная переходная характеристика имеет бесконечную длину во временной области, а передаточная функция имеет дробно-рациональный вид. Такие фильтры могут быть как аналоговыми так и цифровыми.

Способы реализации цифровых фильтров

Различают два вида реализации цифрового фильтра: аппаратный и программный. Аппаратные цифровые фильтры реализуются на элементах интегральных схем, тогда как программные реализуются с помощью программ, выполняемых процессором или микроконтроллером. Преимуществом программных перед аппаратным является лёгкость воплощения, а также настройки и изменений, а также то, что в себестоимость такого фильтра входит только труд программиста. Недостаток — низкая скорость, зависящая от быстродействия процессора, а также трудная реализуемость цифровых фильтров высокого порядка.

Дано:

По номеру варианта (в журнале) записываем параметры для разработки фильтра.

Тип фильтра – ФНЧ

Затухание в полосе задерживания: А – 40 дБ

Частотные характеристики: F₁=1200 Гц

Ширина переходной полосы: Δf=600 Гц

Частота дискретизации: f_д=7200 Гц

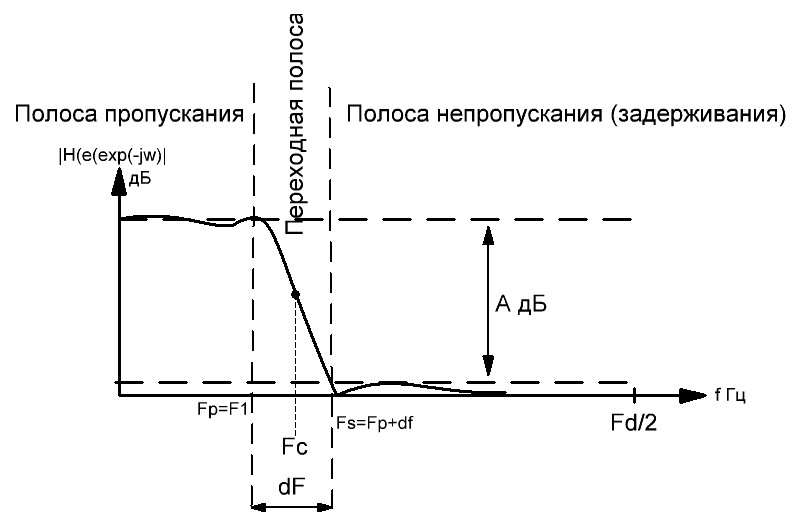
Рисунок 3.1. Допустимые пределы для аппроксимации ФНЧ.

Неравномерность в полосе пропускания и задерживания не рассчитываем.

Расчет фильтра методом весовых окон:

Находим величину нормирующей переходной полосы:

Δf_norm=Δf/f_д=0.0833

Оценим порядок фильра для весового окна Ханна:

N=3.3/Δfnorm=39.6≈40

Порядок фильтра это кол-во отчетов импульсной реакции.

Находим проектную величину среза:

F_p = F1; F_s=F1+Δf=1800 Гц

Fc=(F_p+ F_s­)/2=1500 Гц;

Находим нормирующие частоты:

w1=fc/f_д=0,2083333

комментарии к программе

Функция fir1 реализует вычисления по методу обратного преобразования Фурье с использованием окон:

a=fir1(n,Wn,’ftype’,window,’normalization’)

Здесь:

n – порядок фильтра – целое четное число (кол-во коэффициентов фильтра равно n+1);

Wn – относительная.частота среза (по отношению к частоте Найквиста, равной половине частоты дискретизации Fd) – число в диапазоне (0,1); является вектором из двух чисел, если фильтр полосовой или режекторный;

’ftype’ – тип фильтра (если отсутствует или ‘low’– ФНЧ; ‘high’ – ФВЧ; ‘bandpass’ или отсутствует – полосовой; ‘stop’ – режекторный;

Примечание: в Matlab 5.3 явное указание типа фильтра ‘low’ приводит к отказу от вычислений – в этом случае параметр ’ftype’ нужно опускать. Может оказаться, что по вине разработчиков данная особенность присуща и другим версиям Matlab. Кроме того, возможно, что подобная особенность свойственна и типу ‘bandpass’ (нами не проверялось).

window – вектор-столбец из n+1 элементов (по умолчанию применяется окно Хэмминга hamming(n+1))

‘normalization’ – нормировка АЧХ и ИПХ (по умолчанию значение ‘scale’ – единичное значение АЧХ в центре полосы пропускания; ‘noscale’ – нормировка не производится).

Примечание: при нормализации максимальное значение АЧХ в точности равно единице. При отсутствии нормализации из-за эффекта Гиббса максимальное значение АЧХ больше единицы. Этим и объясняется, что рассчитанные коэффициенты фильтра в отсутствие нормализации больше таковых при наличии нормализации (см.приводимый ниже пример).

Пара команд

[h,t] = impz(a,b,N); % N – число отсчетов ИПХ

stem(t,h)

позволяет вывести на график N отсчетов ИПХ