31.Основные проблемы, возникающие при решении задач векторной оптимизации.

При решении задач многоцелевой оптимизации приходится решать следующие проблемы.

1. проблема нормализации. Данная проблема возникает в связи с тем, что локальные критерии имеют, как правило, имеют различные единицы измерения, что делает невозможным из непосредственное сравнение. Для этого приходится приводить их к единому масштабу и безразмерному виду. Данная операция называется нормированием. Самым распространенным способом нормирования яв-ся:

1) замена абсолютных значений критериев их безразмерными относительными величинами , k=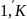

2) Замена абсолютных значений критериев их относительными значениями отклонений от оптимальных значений.

, k=

2. проблема учета приоритета критерия. В этом случае приходится найти математическое значение приоритета и степень его влияния на решение задачи.

3. Проблема определения области компромисса.

32. Методы решения многоцелевых задач.

Методы решения многоцелевых задач делятся на

• методы, кот. основаны на свертывание критериев , k= ;

• методы, в кот. используются ограничения на критерии;

• методы, кот. основаны на отыскании компромиссного решения

Среди них выделяют:

• Метод линейной комбинации частных критериев

• Метод последовательных уступок

• Метод ведущего критерия

• Метод равных и наименьших относительных отклонений

• Метод минимакса

33. Метод линейной комбинации частных критериев. При решении задач данным методом вводится вектор весовых коэффициентов критериев, которые характеризуют важность соответствующего критерия.

.

Тогда целевая функция будет представлять собой сумму частных критериев, умноженных на весовые коэффициенты. При этом критерии в скобке должны быть нормированы.

,

,

.

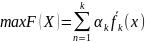34. Метод ведущего критерия. В этом методе все критерии кроме самого важного переводятся в разряд ограничений. Умножив все критерии минимизированной ф-ции на (-1) и обозначив через β=( ) нижние границы соотв. критериев,тогда матем. модель задачи будет иметь вид:

max F(x)= (x); (x)≥ , k= ; (x) , i= , ≥0, j=

35.Метод последов.уступок. В этом методе сначала устан-ся предпочтит-сть вех крит-ев,а на 1-ое место ставится самый важный. Потом по 1-му крит-ю наход-ся оптим.решение и знач-е цел. ф-ции , затем устанав-ся уступка по этому критерию: ∆ ,затем реш-ся задача по 2-му критерию,но с дополн.огранич-ем -∆ (если задача на максимум)

36. Метод равных и наименьших относительных отклонений.

Будем решать задачу по К-критериям:

Запишем условие равенства относительных отклонений значений критериев от их экстремальных значений.

Рассмотрим 4 первых критерия.

По условию задачи f1,f2 – максимизируются, f3,f4 – минимизируются.

Проанализ-м знач-я относит. отклонений первых 2ух критериев.

Если f2*<0 и f1*<0,то тогда

Если f2*>0 и f1*>0,то тогда

Поэтому в равенстве относительных отклонений этих критериев модуль абсолютных величин можно опустить, тогда получим:

Введём обозначения, что

Для критериев f3,f4 получим точно такое же ур-е, т.к. направления их оптимизации совпадают.

Рассмотрим критерии с противоположным направлением оптимизации.

Если f1*<0 и f3*<0,то тогда

Если f1*>0 и f3*>0,то тогда

Поэтому при опускании знака модуля перед одним из выражений ставим «-».

Т.о. для нахождения компромиссного реш-я рассматриваемым методом необходимо оптимиз-ть критерии включённые в число неизвестных задачи и к осн. ограничениям добавить след. ограничения:

, для всех fk, которые как и f1 максимизируются

, для всех fk, которые минимизируются.

37.Метод минимакса. В методе минимакса сначала решается задача по каждому критерию по отдельности,тоесть находятся значения f1*,f2*,…,fk*. Дальше строится целевая функция и дополнительные ограничения.Рассмотрим правила их построения.Предположим,что xj^0,j=1,n –значение компонентов в кампромисном решении .Используя найденное значение функции fk*,k =1,к запишем:относительное отклонение от значений функций в кампромисном решении │(Еcj^k xj^0 – fk*) / fk*│ yk, k = , (1). Среди полученных отклонений выделим наибольшее и потребуем,что бы в кампромисном решении оно было minF = maxyk.Из последнего выражения и вытекает название метода .В формуле (1) заменим отдельные отклонения наибольшим из них,обознача его maxyk=xn +1,тогда получим некоторое неравенство │(E j=1^n cj^k xj^0 –fk*) /fk*│≤ xn+1, k = (2). Т.к. в практических задачах fk >0, k= , то умножим (2) на знаменатель,от чего смысл не нарушится │Е j = 1^n cj^k xj^0- fk*│≤ xn+1 * fk*, k = , (3). Учитывая,что в кампромисном решении значения max-ного критерия<его экстремального значения,а величина min-ного>соответствующего значения,тогда получим. Для max-го критерия Еj=1^n cj^k xj^0 – fk* <0,тогда

│ Е j=1^n cj^k xj^0 – fk*│= -( Еj=1^n cj^k xj^0 – fk*),тогда с учетом последнего выражение (3) запишется

Еj=1^n cj^k xj^0 + fk* xn+1 >= fk* (4)

Для min критериев Е j=1^n cj^k xj^0 – fk* > 0,тогда получим

Еj=1^n cj^k xj^0 - fk* xn+1 <= fk* (5)

Но поскольку кампромисное решение не найдено,то следовательно величины xj^0, j=1,n и xn+1 будем считать неизвестными задачами и обозначать xj, j=1,n+1.Следовательно для нахождения кампромисного решения к исходной системе ограничений добавим ограничения вида (4) Е j=1^n cj^k xj^0 + fk* xn+1 >= fk*,к-относится к max критериям и вида (5).

38. Во всех областях чел. деят-ти встреч. проблемы принятия управ. реш-й в усл-х неопределенности. При этом неоп-ть м.б. связана как с сознательными действиями конкурента, так и др. факторами, влияющими на эфф-ть прин. реш-я. Ситуации, в кот. эфф-ть прин. одной стороной реш-я зависит от действ. др. стор. наз. конфликтными. Теория игр – раздел мат., изуч. конфл. ситуации на основе мат. моделей, т.е. это мат. теория, разраб-я оптим. правило поведения кажд. из участников в конфл. ситуации. Конфл. сит-я наз. антагонистической, если увел-е выигрыша одной из сторон на некот. вел-ну приведет к уменьш-ю выигрыша др. ст. на такую же вел-ну и наоборот. Стратегия игрока – сов-ть правил, однозначно опред-щих послед-ть действий игрока в конкр. конфл. сит-и. Стратегия игрока наз. оптим., если она обеспеч. данн. игроку при многократном повторении игры максим. возм. средний выигрыш или миним. возм. средний проигрыш независ. от поведения конкурента. Партией наз. каждый вариант реализации игры опред.обр. выбор одной из стратегий и ее реализ-я наз. ходом. Ход наз. личным, если игрок сознательно выбир. 1 из стратегий. Ход наз. случ., если выбор осущ-ся в случ. механизме. В зав-ти от кол-ва уч-ков игры подразд. на конечные и бескон. В конце партии кажд. игрок A_i, i= получ. некот. сумму a_i, i= , кот. наз. функцией выигрыша (плат. ф-я). Ф-я выигрыша мож. выр-ся как колич-но, так и выражением. Если a_i>0, то это говорит о выигрыше i- игрока. Если a_i<0 проигр., a_i=0 – ничья. В зав-ти от вида ф-и выитгрыша игры подразд. на матричные, биматричные, непрерывные, выпуклые и т.д.

39. Матричные игры с нулевой суммой. Будем рассматривать парные конечные игры, т.е. у каждого из 2х игроков А и В конечное число стратег. В большинстве случаев мы имеем игры с нулевой суммой, т.е. игры, в которых выигрыш 1го игрока равен проигрышу другого.

Парную конечную игру удобно исследовать, если она записана в виде платежной матрицы:

А\В	В1	В2	…	Bn
А1	а11	a12	…	a1n
А2	а21	а22	…	a2n
…	…	…	…	…
Am	am1	am2	…	amn

Здесь каждое число аij, i=1,m j=1,n является действительным числом и представляет собой сумму выигрыша, уплачиваемую игроком В игроку А, если игрок А выбирает стратег. соотв. i-той строке, а игрок В выбирает стратег. соотв. j-тому столбцу. Такую игру называют матричной игрой размерности m на n. Целью участников любой матричной игры, явл. выбор наиб. выгодной стратег., кот. доставляют А max выигрыш, а В – min проигрыш. Чистая стратегия – Аi, i=1,m игрока А (Bj, j=1,n игрока В) назыв. Возможный ход игрока А (В) выбранный им с вероятностью 1. Если игра состоит из матричных ходов, то выбор пары чистых стратег. (Ai, Bj) единственным образом определяет исход игры. Если в игре исп-ся случ. ходы, то исход игры определяется математическим ожиданием (ср.знач.). Стратег. А назыв. оптимальной, если при ее применении выигрыш игрока А не , какими бы стратег. не пользовался игрок В. Оптим. стратег. для В явл. стратег., при которой проигрыш игрока В не , какими бы стратег. не пользовался игрок А.

40. Решение матричных игр в чистых стратегиях. Если игрок А имеет m, а игрок В – n стратег., то для любой пары стратег. игроков, их чистые стратег. можно представить в виде единичных векторов. Например, для пары стратег. (Ai, Bj) – ед.вектор: pi=(0…0,1,0…0) и qj=(0…0,1,0…0). При нахождении оптим.стратег. игроки исп-т принцип осторожности, при кот.игроки считаются одинаково разумны, используя этот принцип, найдем оптим.стратег. А и В.

Игрок А для каждой стратег. Аi, i=1,m, сначала найдет min знач. выигрыша: αi =min(j) aij,i=1,m Затем среди αi выберем max: α= max(i) αi .

Величина α назыв. нижней чистой ценой игры (максимином): α = max(i) min(j) aij

α гарантированный выигрыш, кот.может обеспечить игрок А, при любом поведении В. Стартег. Аi* обеспеч.получение нижней цены игры – максиминная стратег. Игрок В для кажд.стретег. Bj j=1,n, выберет max значение: βj= max(i) aij, j=1,n

Затем из βj выберет min знач.: β= min(j) βj Стратег. Bj* обеспеч. верхнюю чистую цену игры и назыв. минимаксом

Теор. 1: В матричн.игре нижн. цена игры не превосходит верхн.чист.цены игры, т.е. α <= β

Док-во: По определению αi =min(j) aij <= aij и βj= max(i) aij >= aij, значит объединим последнее в соотнош: αi =min(j) aij <= aij <= βj= max(i) aij, а след-но αi<= aij<= βj или αi <= βj. Данное нер-во справедливо при любых комбинациях i и j, оно будет справедливо и для тех i и j, для кот. α= max(i) αi и β= min(j) βj след-но для этих i и j α <= β

41. Если в матрич. игре ниж. и верх. чистые цены совпад-т, т.е.α=β,то такие игры наз.играми с седловой точкой.Знач-е υ=α=β наз.чистой ценой игры,а стратегии наз. оптимальными чистыми стратегиями. Пара чис.стр-гии ( )наз. седловой точкой матрич.игры. Элемент наз.седловым элементом платёж.матрицы.Признаком матрич.игры с седловой точ. явл.выраж. = = Элемент явл.наименьшим в строке и наиб-м в столбце Решением явл.тройка чисел( )

42. Решение матричных игр в смешанных теориях. Смеш. страт. А(В) – вектор: р(А)=(р₁,…,р_m), р_i≥0, i=1,m и ∑р_i=1 (q(B)=(q₁,…,q_n), q_j≥0, q=1,n, ∑q_j=1). Т.к. А и В выбирают свои чистые страт. случайно и независимо друг от друга, т.е. А выбирает страт. А_i с вероятностью p_i, а В выбирает В_j с вероятностью q_j=>вероятность комбинации (А_i,В_j)= p_iq_j.

Значит, случайной будет и величина выигрыша А (проигрыша В).

Мы будем вести речь о ср. величине (мат. ожидании), кот. является функцией от смеш. страт. и определяется по формуле f(p*,q*)=∑_i=1^m∑_j=1ⁿ a_ij*p_iq_j. Смеш. страт. – оптимальная, если для произвольных стратегий р=(р₁,…,р_m) и q=(q₁,…,q_n) выполняется след. нерав-во: f(p,q*)≤f(p*,q*)≤f(p*,q) (1)

Из этого нерав-ва =>, что в седловой т. p*q* платёжная функция f(pq) достигает max по смеш. страт. р и min по страт. q. Значения плат. функции при оптим. смеш. страт. и определяет цену игры: υ=f(p*q*)

Теорема2. В смеш. страт. любая конечная матричная игра имеет седловую точку.

Теорема3 (о необходимом и достаточном условии смешанных стратегий) Чтобы смеш. страт. p*q* игроков А и В в игре с матрицей [a_ij]_m×n и ценой игры υ были оптим., необходимо и достаточно выполнение нерав-в: ∑_i=1^ma_ij×p_i*≥υ, j=1,n (2) ∑_i=1^ma_ij×q_j*≤υ, i=1,m (3).

Док-во: Необходимость=>Пусть p* и q* - оптим. смеш. стратегии. Покажем, что для них будут выполнены (2) и (3).

Воспользуемся определением оптим. смеш. страт., для кот. выполняется (1).

Запишем её в развёрнутой форме: ∑_i=1^m∑_j=1ⁿ a_ij×p_iq_j*≤υ≤∑_i=1^m∑_j=1ⁿ a_ij×p_i*q_j (4).

В правую часть (4) подставим вектор q_j=(0,…,0,1,0,…,0).

Получим ∑_i=1^m∑_j=1ⁿ a_ij×p_i*q_j=∑_j=1ⁿ q_j(=1) ∑_i=1^ma_ij×p_i*=∑_i=1^ma_ij×p_i*≥υ (доказано, что оптим. смеш. страт. р* удовлетвор. нерав-ву (2)).

Достаточность=>Пусть выполняются нерав-ва (2) и (3).

Докажем, что p* и q* - оптим. смеш. стратегии. Т.е. имеет место соотношение (4).

Докажем, что из нерав-ва (2) следует правая часть (4).

Пусть q=(q₁,…,q_n) – произвольный вектор. Тогда: ∑_i=1^m∑_j=1ⁿa_ij×p_i*q_j=∑_j=1ⁿq_j∑_i=1^ma_ij×p_i*≥ ∑_j=1ⁿq_jυ=υ∑_j=1ⁿq_j= υ

Итак, ∑_i=1^m∑_j=1ⁿa_ij×p_i*q_j≥ υ, а это и есть правая часть (4).

Аналогично док-ся, что из нерав-ва (3)=>левая часть(4). Т. о. доказано, что из (2) и (3)=>(4). А это говорит об оптим-ти смеш. страт. p* и q*.

Из данной теоремы можно сделать вывод, что для проверки того, что набор (p*,q*, υ) является решением матричной игры. Достаточно проверить, удовлетворяют ли смеш. страт. p* и q* (2) и (3), а также уравнению ∑_i=1^m p_i*=1, ∑ _j=1q_j*=1.

Из данной теоремы следует: 1. Если игрок А применяет свою оптим. смеш. страт. р*, а В – любую чистую срат. b_j*, то выигрыш А будет не меньше цены игры υ.

2. Если В применяет свою оптим. смеш. страт. q*, а А – любую чистую страт. a_i, то проигрыш В не превысит υ.

43. Теорема о преобразованиях элементов платежной матрицы. Если один из игроков придерживается своей оптимальной смеш-й стратегии, то его выигрыш остается постоянным и = цене игры, независимо от того, какую стратегию применяет другой игрок, если только тот не выходит за пределы своих активных стратегий.

Доказательство: Пусть набор (p*, q*, v) является решением матричной игры [a_ij]_m×n, при этом игрок А имеет r активных стратегий, игрок В – k стратегий. Перенумеруем чистые стратегии игроков так, чтобы активные оказались первыми, получим: p*=(p₁*, p₂*,…, p_r*, 0,…,0), где ; q*=(q₁*, q₂*,…, q_k*, 0,…,0), где . Пусть игрок А придерж-ся своей оптимальной смеш-й стратегии р*, а игрок В чистой стратегии, тогда согласно теореме 3 получим: 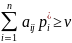, (5). Если игроки А и В используют свои оптимальные смеш-е стратегии, то выигрыш игрока А = цене игры v, где , учитывая неравенство (5), получим: . Последнее соотношение выполнимо лишь в случае, когда неравенство (5) превращается в равенство, отсюда можно сделать вывод, что для любой смешанной стратегии q=(q₁, q₂,…, q_k, 0,…,0) будет выполняться равенство , что и доказывает теорема. На основании данной теоремы решение матричной игры можно упростить, для этого надо определить доминирование одних стратегий над другими. 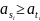Игрок А заинтересован в максимизации выигрыша, сравнивая элементы строк s и t, если получим, что , то в этом случае выигрыш игрока А при стратегии А_s будет больше, чем при стратегии А_t. В этом случае стратегия А_s доминирует над стратегией А_t. Стратегия А_s – доминирующая, а А_t – доминируемая. Т.к игрок В заинтересован в минимизации проигрыша, то сравнивая элементы столбцов r и l, для которых , то проигрыш игрока В для стратегии В_r будет меньше, чем для стратегии В_l. В_r доминирует над В_l. В_r – доминирующая, В_l – доминируемая.

Если все элементы строки (столбца) в каких-либо стратегиях равны, то такие стратегии называются дублирующимися, и их можно удалять.

44. Если p∗ и q∗ оптимальные смешанные стратегии, соотв-но игроков A,B в матричной игре [aij]m×n и ценой игры υ, то эти стратегии будут оптимал-ми и в матрич-ой игре [𝑏𝑐𝑖𝑗+c]m×n и ценовой игры υ΄=bυ+c. Док-во: Умножим последнее нерав-во на полож-ое число b и к обеим частям нерав-в и прибавим произведение: c т.к то получим: . Теорема доказана для оптим-ой смешан-ой стратегии p͊ игрока A, аналогич-но доказ-ся теорема для q͊ игрока B. На основ-ии этой теоремы платеж-ую матрицу игры, имеющ. отриц.числа можно преобраз-ть в матрицу с полож-ми числами.

45. Сведение матричной игры к задаче линейного программирования. Решение матричной игры сведением к задаче линейного программ-ния. Пусть имеем матричную игру размерности m х n:

Обозначим через p* и q* оптимал. смеш. стратегии игроков А и В. Оптим. смеш. стратег. Р* игр А гарантирует ему выигрыш не меньше независимо от того, какую из чистых стратегий выбирает игрок В.

=1

Оптим.смеш.стратег. q* гарантир.игр. В проигрыше не больше цены игры независимо от выбора чистой стратег.игроком А.:

Все элементы плат. матрицы можно сделать положит. Значит цена игры >0.

Преобразуем 1 и 2, разделив обе части на и введём обозначения, что

, i=1,m⁻,

(4)

Т.к. игрок А стремится максимиз. Цену игры В, то тогда обратная величина будет минимизир. След-но, оптим.стратег.игрока А находится из задачи:

Аналогично рассуждая оптим. стратег.игрока В найдём из задачи.

Решив эти задачи, мы сможем опр-ть : ; ; .

46. Игры с природой. Понятие риска статистика. Матрица рисков. Управление экономическими процессами и явлениями осуществляется путем последовательности принятых решений. В случае отсутствия достаточно полной информации возникает неопределенность в принятии решений. С целью уменьшения неблагоприятных последствий в каждом конкретном случае следует учитывать степень риска и имеющуюся информацию. В этом случае, лицо, принимающее решение – статистик – вступает в игровые отношения с некоторым абстрактным лицом, которое будем называть природой. Под природой будем понимать совокупность неопределенных факторов влияющих на эффективность принимаемых решений.

Статистик должен уметь находить управленческие решения, когда природа не выбирает сознательно свои оптимальные стратегии. Но иногда мы располагаем вероятностными характеристиками состояния природы. Такого рода ситуации принято называть играми с природой.

Множество стратегий статистика будем обозначать через А, а отдельную стратегию через . Множество состояний природы будем обозначать через П, а отдельное состояние через .

Во взаимоотношении с природой статистик может использовать любую из стратегий в зависимости от состояния природы. Причем статистик, когда определяет, какую стратегию ему выбрать руководствуется некоторым поведением, которое и будет являться оптимальной стратегией. При этом статистик может пользоваться как чистой, так и смешанной стратегией. Обозначим платежную матрицу игры с природой через:

,

где каждый элемент называется выигрышем статистик, если он применяет стратегию при состоянии природы (эффективность комбинации ( )).

При анализе игры с природой вводится также показатель, позволяющий оценить, насколько то или иное состояние природы влияет на исходную ситуацию. Этот показатель называется риском.

Риском статистика, когда он пользуется чистой стратегией при состоянии природы называется разность между максимальным выигрышем max , который он мог бы получить достоверно зная, что природой будет реализовано состояние и тем выигрышем , который он получит используя стратегию не зная, какое из состояний природа действительно реализует.

.

47.Критерий Байеса и Лапласа выбора наилучшей стратегии статистика. При решении задач используются 2 группы критериев. К 1-й относится группа критериев, в которой используются вероятности состояния природы. К этой группе относятся критерий Байеса и Лапласа. В качестве оптимальной по критерию Байеса принимают чистую стратегию, при которой максимизируется средний выигрыш статистика:

Max .

Если статистику предоставляется в равной мере правдоподобные все состояния природы, т.е. , то по критерию Лапласа в качестве оптимальной берется стратегия, обеспечивающая:

48. Критерии Вальда, Сэвиджа и Гурвица выбора наилучшей стратегии статистика. Эти критерии прим. при неизвестных априорных вероятностях состояний природы. В этом случае статистик принимает решение на основе анализа либо платежной матрицы, либо матрицы рисков. Критерий Вальда – это макс. крит., и его можно сформулировать как для чистых, так и для смешанных стратегий. Кр. Вальда явл. кр-ем крайнего пессимизма, т.к. здесь статистик исходит из предположения, что «природа» действует против него наихудшим образом, т.е. реализует такие состояния , при кот. величина его выигрыша приним. наим. знач. Исходя из этого статистик выбирает такую чистую стратегию , при кот. наим. выигрыш будет макс., т.е. обеспечивается максимин . Говоря иначе оптимальной по кр. Вальда будет его максиминная чистая стратегия, а макс. выигрышем – нижняя чистая цена игры Для смешанных стратегий кр. Вальда формулируется следующим образом: оптимальной смешанной стратегий статистика ) счит. та, при кот. его миним. сред. выигрыш максим-тся.

Кр. Сэвиджа, как и крит. Вальда, явл. крит. крайнего пессимизма, ибо и здесь статистик исходит из предположения, что природа реализует самые неблагоприятные для него состояния. Крит. Сэвиджа рекомендует выбирать в качестве оптимальной ту чистую стратегию , при кот. минимиз. величина максим. риска, т.е. . При использ. крит. Сэвиджа в области смешанных стратегий вместо среднего выигрыша (как было в кр. Вальда) рассм-тся средний риск. Самым неблагоприятным для статистика явл. такое сост. природы, при кот. величина среднего риска достигает наиб. знач. Кр. Сэвиджа рекомендует в качестве оптимальной выбир. ту смешанную стратегию , при кот. максим. знач. среднего риска минимиз. Кр. Гурвица, называемый кр-ем пессимизма-оптимизма, рекомендуют рассчитывать на нечто среднее. В области чистых стратегий оптим. счит. стратегия, найденная из условия:

max (по i) , где и выбирается из субъкт. соображений. При кр. Гурвица превращ. в кр. Вальда (крайнего пессимизма):

max (по i) min (по j) ; при - в критерий крайнего оптимизма:

max (по i) min (по j) ; при получ. нечто среднее.

Подчеркнем, что анализ практических ситуаций следует проводить по нескольким критериям, что позволит глубже вникнуть в суть явления и выбрать обоснованное решение.

49. Модели анализа основ-х финан-ых операций. Пусть Р – начальный капитал, положенный в банк при годовой %-ой ставке r. Тогда в конце периода капитализации наращенная сумма, т.е. сумма капитала и наросшего % составит Р*(1+r), где r – выражена в долях.

В конце второго периода капит-ции наращенная сумма составит [P*(1+r)]*(1+r)=P*(1+r)².

В общем случае наращенная сумма за n-периодов капитализации будет равна S=P*(1+r)ⁿ .

Наращенная сумма – будущая стоим-ть началь-го капитала и обознач-ся FV.

Коэффиц-т α равный α=(1+r)ⁿ – коэффиц-т аккумуляции, который показывает денеж-ю сумму, нарастающую за n – периодов капит-ции при начальном капитале 1д.е. Из формулы след-т, что P=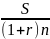 , т.е. для того, чтобы сумма наращенная за n – периодов капит-ции составила S д.е. в начале срока нужно положить в банк д.е. Такой началь-й капитал обеспеч-щий заданную наращенную сумму назыв-ся текущей стоим-тью суммы S и обознач-ся PV. Следов-но, PV= .

Процесс нахождения текущей стоим-ти наз-ют дисконтир-ем. Коэффиц-т δ=(1+r)^-n наз-ют коэффиц-ом дисконт-ния, кот. показ-ет какую сумму нужно положить в банк для того, чтобы через n – периодов капит-ции наращенная сумма составила 1 д.е.

50. Дисконтирование денежных потоков. Текущая стоимость проекта. Инвестиционный проект – любое инвестирование денег, генерирующее денежные потоки в будущем. Метод дисконтирования денежных потоков инвестиционного проекта является ключевым в современном финансовом анализе, при этом дисконтируются свободные денежные потоки, которые представляют собой разность прибыли и инвестиций в заданном периоде времени.

Предположим, что инвестиционный проект генерирует положительные свободные денежные потоки в течение n-периода времени:

Начальные инвестиции в проект равны , временную диаграмму свободных денежных потоков можно представить в виде:

Своб. ден. потоки ……..

Время 0 1 2 n-1 n

Вместо того, чтобы инвестировать деньги в проект, инвестор может положить некоторую сумму в банк под процент с целью получения таких же денежных платежей в будущем.

Текущей стоимостью свободных денежных потоков инвестиционного проекта называется начальный капитал, положенный в банк под процент, обеспечивающий последовательность денежных потоков, равных денежным потокам инвестиционного проекта и определяется по формуле:

Таким образом, текущая стоимость инвестиционного проекта равна сумме дисконтированных денежных потоков.

Процентная ставка, используемая при дисконтировании свободных денежных потоков проекта, называется нормой (ставкой) дисконтирования. Банк процентную ставку может брать в качестве нормы дисконтирования только в том случае, когда риск, связанный с денежными потоками проекта и риск, связанный с банковскими депозитами одинаков.

51.Чистая текущая стоимость инвестиционного проекта. Проанализируем выгодность вложенных денег в проект по сравнению с вложением в банк.

Чистая текущая стоимость проекта (NPV) представляет собой разность между текущей стоимостью проекта и начальными инвестициями и показывает на сколько меньше денежных единиц необходимо в начальный момент времени вложить в проект, чем в банковский депозит, чтобы обеспечить последовательность денежных платежей, равных свободным денежным потокам проекта.

NPV=PV- Если NPV 0, то проект эффективен, если NPV 0, то проект неэффективен, если NPV 0, то это значит , что следует использовать другие критерии эффективности.

52.Внутренняя норма прибыли проекта. IRR-такая %-ая ставка, при которой банковский начальный капитал, обеспечивающий последовательность платежей = свободным денежным потокам проекта, равного начальным инвестициям в проект, т.е. это такая норма дисконтирования, при которой чистая текущая стоимость=0.

Если IRR >r, то проект следует принять, если IRR <r, то –отклонить, если IRR = r, то вложения в проект окупаются

Пример: I0=600 ден. ед., С1=300 ден. ед., С2=500 ден. ед.; ; IRR = 19,64 %.

Следовательно при годовой %-ой ставке 19,64% банковский начальный капитал 600 ден. ед. обеспечит выплату платежей = свободным денежным потокам проекта.

53.Индекс прибыль-ти(ИП)-оценивает относит –ю прибыльность проекта, т.е. приб-ть с каждой вложенной ед-цей проекта.PI=PV/I₀.Если ИП > 1,то проект эффективен;Если ИП < 1,то не эфф-вен;Если PI=1,то следует исп-ть др.методы оценки.Период окуп-сти(ПО)-опред-ся так:PP=min n, при кот. ≥ I_0.Дисконт-ный ПО(ДРР) опред-ся след.образом:ДРР=min n,при кот. ≥ I_0. Понятно,что ДРР всегда больше РР.

54. Пусть потребит корзина состоит из m видов благ. Обозначим через - количество k-го блага в потребит корзине, -рыночная цена единицы k-го блага в начале периода времени, – рыночная цена единицы k-го блага в конце периода. Тогда цены потребит корзины в начале и конце периоды равны. ,

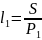Уровень инфляции за период будет опред по формуле: . Пусть P – начальный капитал, а r - банковская процентная ставка за период времени. Тогда наращенная сумма за период составит S=P(1+r).процентная ставка называется номинальной . в начале периода времени за начальный капитал можно приобрести потребительских корзин. А в конце периода - потребительских корзин. Реальная %-я ставка будет определяться по формуле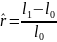 .в отличии от номинальной %-й ставки реальная учитывает инфляцию. Найдем как реальная %-я ставка определяется с помощью номинальной и уровнем инфляции. . Инфляция влияет на внутреннюю норму прибыли проекта. Поэтому при нахождении чистой текущей стоимости проекта следует учитывать инфляцию. Из последней формулы можно найти номинальную %-ю ставку, кот использ для определ нормы дисконтирования своб денежных потоков:

55.Модель оптим.портфеля инв.проектов. Рассмотр.возм-ть реализ-и n-проектов.Эф-ть і-го проекта хар-ся чистой текущ.ст-тью NPV;i= i= . Нач.инв-ии в і-тый проект=Іо, i= .Общее кол-во имеющ.фин.рес-в=і. Обозначим ч/з х решение о реализации либо откл-ние і-го проекта. Данные значения равны. X₀={ –0,если проект отклонен;1,если проект приним. ЭММ будет иметь вид:

max F = ; x;

x_iє

i=

57.Анализ чувствит.ден.потоков проекта. Анализ чувствит-ти ден.потоков инв.проекта-это анализ того,как измен.ден.потоки проекта при измен-и 1го или неск.влияющ.на них факторов. Рассм.методику анализа на примере.

58. Основные понятия СПУ. При планировании сложных комплексов взаимосвязанных работ и оперативном управлении ходом их выполнения наиболее эффективный метод – метод СПУ.

Данные методы появились в конце 50-х годов 20века. В основе методов СПУ лежит графическое представление проекта в виде сетевого графика. Сетевой график – ориентированный граф (G; орграф), который содержит вершины Е₁, Е₂… и дуги е₁,е₂… Вершины будут отождествляться с событиями, а дуги – с работами. Работы – любые действия, трудовые процессы, которые сопровождаются затратами ресурсов или времени. На сетевых графиках работы обозначаются стрелками. Работами также считаются технологические процессы, которые, например, потребляют только время. Под работами также могут пониматься фиктивные работы, которые показывают, что одна работа не может совершаться раньше другой. На сетевом графике они обозначаются пунктирными стрелками. Событие обозначает факт окончания всех работ в него входящих или начало работ из него выходящих. Событие не имеет протяженности во времени. На сетевых графиках они обозначаются геометрическими фигурами. Событие, которое начинает выполнение проекта, называется исходным – оно не имеет предшествующих работ. Событие, которое завершает проект, называется завершающим – оно не имеет последующих работ. Все остальные события называются промежуточными. На сетевых графиках надо работами указываются числовые характеристики: время выполнения работы, количество ресурсов и так далее.

59.Правила построения сетевых графиков. Прежде, чем представить сетев. график необх. сост-ть перечень работ, оценить продолжит-ть каждой работы, установить послед-ть работ и т.д. Такой перечень удобно представить в виде структурно- временной таблицы.

работы	Предшест. работы	Время
	-	2
	-	4
		3
		2
		5
		7
		3

Правила нумерации событий:

1)исход. вершину относим к рангу 0 присваиваем ей №1

2)вычеркиваем все дуги, выходящие из вершины 1 и отнесем все события, кот. появились без входящих дуг к 1-ому рангу. Эти события нумеруем дальше в порядке 2,3 и т.д.

Работы удобно обознач. номерами нач. и конеч. событий =(1,2), =(3,4).

Правила построения сетев. графиков:

1. На сетев. графиках не дожно быть тупиков, т.е. событий, из кот. не выходит ни 1 работа, за исключ-ем завершающего события.

2. На сетев граф.не должно быть событий, кроме исходного, которому не предшествует хотя бы 1 работа.

3. При построении сетев. граф. нельзя допускать, чтобы 2 смежных события были связ. 2-умя или большим количеством работ. Такая ситуация возникает при изображении параллельно выполняемых работ. В этом случае, чтобы избежать путаницы в обознач-и работ рекоменд-ся вводить дополнит промежут. события.

4. В сетев. граф. не должно быть циклов

5. Е сли к-либо сложные работы могут быть начаты до полного окончания предшествующей им работы, то последняя изображ-ся как ряд последовательно выполн-ых работ, каждая из к-рых завершена событием.

6. Если для выполнения одной из работ необх-мо получение рез-тов предшеств. работ, то должно быть введено дополнит. новое событие, к-рое отражает рез-т выполнения этих работ, а также должна быть введена фиктивная работа.

60.Расчет врем.параметров событий. К осн.параметрам сетевого графика отн-ся:продолжит-ть выполн-я всего проекта,времена свершения соб-ий,сроки выполн-я работ и их резервы времени. Длина пути из события i в j поним-ся как продолжит-ть выпол-я всей послед-ти работ, составл. этот путь. Путь, в кот. нач.вершина совпадает с исх. событием, а конечное с завершающим наз. полным. Путь от исходного события до любого промежуточного наз. предшеств. событию путем. Путь от дан. события до завершающего наз. последующим путем. Критический путь – путь, имеющ. наиб. продолжительность. Работы и события, леж. на крит. пути наз. критическими. Крит.время – суммарная продолжительность работ, принадл. крит пути. Lкр – крит путь; t_кр – крит.время

Ранним сроком свершения события j наз. самый ранний момент времени, к кот. заверш. все предш. этому событию работы. T(р) _j = max (tp(i) + t_ij) (1); (i,j)€V⁺_j , j= , где V⁺_j – множесвто всех работ, вход. в j-тое событие.

Поздним сроком сверш.соб. i наз. самый поздний момент времени, после кот. остается ровно столько времени, ск-ко необ-мо для завершения всех работ след. за этим событием. T(п) _i = min (tп(j) - t_ij) (2); (i,j)€V⁺_j , i= .

Для событий крит. пути ранние и поздние сроки сверш. совпад. Резевром времени соб. i наз. разность м/у поздни и ранним сроками сверш. соб-й. R(i) = t п(i) – tр(i)/

Поскольку ранние и поздние сроки крит. соб. совпадают, то резервы крит. соб. = 0

Р

ааа

анние и поздние сроки сверш. соб. м. находить на сет. графике. Для этого используется 4-х секторной схемой:

Алгоритм:

1.Подставляем в верхних секторах номера событий.

2.Рассматривая события в порядке возр. номеров и имея в виду,что tp(1)=0, по формуле (1) определяем, tp(j), j=2,n

3.Начиная с конечного события, для кот. tn(i)=t_кр по формуле (2) определяем tn(i), i=1,1-n и записываем в правом секторе.

4.В нижнем секторе запис. резервы времени событий.

61. Расчёт временных параметров работы. Ранний срок начала работы (i,j) = раннему сроку свершения события i.

Поздний срок окончания работы (i,j) совпадает с поздним сроком свершения события j.

Ранним сроком окончания работы (i,j) будем называть сумму раннего срока начала этой работы и её продолжительности. Поздним сроком начала работы (i,j) будем называть разность между поздним окончанием данной работы и её продолжительностью. . Полными резервами времени работы (i,j) назыв. максимально возможный запас времени, на кот. можно отложить начало работы или увеличить время её выполн-я без увелич-я времени выполн-я работы. .

62.Линейный график Ганта. Для небольших комплексов работ удобным дополнением к сетевому графику явл. линейный график. На лин. графике каждая работа изобр. горизонт. отрезком, длина кот. В соотв. масштабе = продолж. работ.

Начало к. работы совпадает с ранним сроком сверш. ее нач. события. Работы изобр. в той же послед-ти, что и на сетевом графике. По линейному графику строится диаграмма потребления ресурсов (эпюра).

График

63. Пусть задан срок выполнения проекта t₀, а расчетное время t_кр.>t₀. В этом случае оптимизация коплекса работ сводится к сокращ-ю продолж-ти критич-го пути. Это сокращение м. б. достигнуто либо за счет перераспределения внутр. резервов, либо за сч. привл-я доп. ср-в. Рассм. 2 постановки задачи оптимиз-и проекта по времени с исп-ем доп. ср-в. Задача1. Пусть задан сетевой график проекта G=(E, 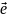). Время выполнения каждой работы обозн. ч-з t_ij. Вложение доп. ср-в x_ij в работу (i, j) сокращает ее выполнение до значения t’_ij =t_ij – x_ijk_ij, где k_ij – технологические коэфф. использ-я доп. ср-в. Сокращ-е продолж-ти работы не беспредельно. Сущ-ет миним. возможн. вр. его выполнения d_ij. Требуется найти вел-ны доп. вложений в кажд. работу x_ij, а также время начала и оконч-я кажд. работы, чтобы общая сумма привлеч-х доп. ср-в была миним., а время выполн-я всего комплекса работ не превосх. t₀. minF= ; 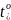≤t₀, (i,n)ϵ ; - ≥d_ij, (i,j)ϵ ; - =t_ij-x_ijk_ij, (i,j)ϵ ; ≥ , (i,j,r)ϵE, x_ij≥0, ≥0, ≥0, (I,j)ϵ

64. Отимиз. пр-та по вр. за счёт влож-я выделенной ∑ ср-в. Задача закл. в max возм-м сокращении срока выполнения проекта за счёт ∑ доп. ср-в не превыш. В.

t_кр = t⁰_n-1,n → min

∑x_ij ≤ B

t⁰_ij - t^н_ij ≥ d_ij , (i,j)€e^→

t⁰_ij - t^н_ij = t_ij -x_ij∙k_ij, (i,j)€e^→

t^н_jr ≥ t⁰_ij , (i,j,r)€E

Если проект будет завершать несколько работ, то необходимо добавить фиктивн. раб. (n, n+1), время вып-я кот.=0, т.е. t⁰_n,n+1 – t^н_n,n+1=0, тогда ЦФ будет иметь вид:

t⁰_n,n+1→ min

65. Оптимиз. пр-та по ст-ти при нефиксир.величине крит. пути. Пусть для кажд. раб. известны след. данные:

d_ij- min продолж-ть вып-я работ, кот. соотв. наиб. затраты С_ij; D_ij- нормальная продолж-ть, кот.будут соотв.наим. затраты c_ij. Будем считать, что затраты на отд. виды работ нах-ся в обратн. завис-ти от прдолж-ти их выполн.

Коэф-ом доп. затрат (КДЗ) будем считать коэф-т, кот. нах-ся по ф-ле: h_ij = (C_ij-c_ij)/(D_ij-d_ij)

и показ. на сколько увелич. ст-ть работ (ij) при уменьшении вр-ни её выполн. на 1 ед.

Задача: Пусть задан сет.гр-к проекта G=(E;e^→). Для кажд раб. изв-ны продолж-ть и ст-ть выполн. в нормальн. и срочном режимах. Если все раб. вып-ся в норм. режиме, то крит. срок будет наиб., а ст-ть – наим. Необходимо сокр. крит. срок до некоторого min возм. значения при min возрастании ст-ти проекта.

Алгоритм: Предварит. шаг. По данным задачи опред. КДЗ h_ij. Используя нормальные продолж-ти работ нах-м крит. путь L_кр, t_кр и полные резервы некрит. работ R_n, а также опред-м затраты на реализ. проекта С.

Общий шаг. 1)среди крит. работ нах-м работу, для кот. КДЗ наим. Если эта работа явл. общ. для всех крит. путей или крит. путь один, то она и подлежит сокр-ю.Если найденная работа не явл. для крит. путей общей, однако крит. пути имеют одну или неск. общих работ, то на кажд. из параллельн. участков крит. путей нах-м раб. с наим КДЗ, суммир-м КДЗ этих раб. и сравн-м с КДЗ той раб., для кот. он наим. Если ∑ КДЗ работ не больше КДЗ общей раб., то эти 2 раб. и подлеж. сокр-ю. Если ∑ КДЗ равна КДЗ общей раб., то сокр-ю подлеж. все 3 раб. Если КДЗ общей раб. меньше ∑ КДЗ работ, то сокр-ю подлеж. общая раб. Если крит. пути не имеют общих раб., то на кажд. из них нах-ся раб. с наим. КДЗ, кот. подлеж. сокр-ю.; 2)сокращая продолж-ти работ на такую величину, чтобы они достигли min продолж-ти или образов. новый крит. путь (если полн. резерв одной из некрит. раб. станет =0); 3)для нового сет. граф. опред. Lкр, tкр, R_n(ij), C; 4)проверяем все ли раб. крит. пути достигли min продолж-ти. Если да, то задача решена, если нет- переходим к пункту 1).

66.Пусть задан сетевой граф.проекта.Извес. продол-ти вып-ния раб-т и их стоим-ть в срочном режиме( ).В этом случае ст-ть проекта будет наиб-й,а время вып-ния наим-м.Нужно миним-ть стоим-ти проекта за счёт увел. времени отдельных раб-т при фиксиров.сроке .В этом случае может быть меньше заданного срока или рав-ся ему.Если = ,то оптимиз-ция возможна только за счёт резервов некритич.раб-т,а если < –резервов всех раб-т проекта. После оптим-ции все работы будут критическими.т.к. их продол-ти будут достигать наиб.возможных знач-й.Ни одно событие,ни одна раб.не будут иметь резервов-такой план наз.безрезервным.Здесь ранние и поз. сроки свершен-я собитий будут сов-ть,а время нач.и окон.раб-т будут сов-ть со сроками свершения событий.Поэтому неизв-ми задачи будут счит-ся сроки свершения событий.Продол-ть вып-ния каж.раб-ты в оптимальном плане опред-ся как раз-ть ,а ст-ть вып-ния работ опред-ся по фор-ле: Мат.модель з-чи примет вид: =∑((i,j)∈ ) [ ; ≥ ,(i,j) ; =0,

67.Оптимизация проекта по ресурсам. Осн. задача при планир-ии. Пусть задан сетевой гр. проекта G=(Е, ē). Кол-во ресурсов =R. Для каждой работы будут приписаны 2 числа:

1. Продолжит-ть выполн-я работы t_ij

2. Интенсивность потребления рес-са r_ij. Т.е. кол-во рес-са, которое необход.

Для выполн-я (ij). Требуется так разместить работы во времени, чтобы в любой момент времени было достат. кол-во рес-сов и при этом время выполн-я всего комплекса работ было min.

Алгоритм:

Предварит. шаг: по сетевому гр. составляем лин-ый гр., по которому определяем критич. путь.

1. проектируем на ось времени начало и конец каждой работы на каждом временном отрезке определяем суммарное кол-во потребляемого рес-са.

2. Рассм-ем отрезок [t₀,t₁], над этим отрезком рассм-ем все работы. Нумеруем их в порядке возраст-я их полных резервов во времени. Работы с одинак. Полными резервами –в порядке убыв-я интенсивности.

3. В порядке присвоенных номеров послед-но суммир-ем интенсивность работ и сравниваем полученые суммы с заданной величиной рес-са R.если после прибавления интенсивности очередной работы сумма превосходит R, то это работа сдвигается вправо на величину рассмотренного отрезка. Преходим к добавл-ю интенсив-ти очередной работы.

Ощий шаг: Рассм-ем отрезок [ t_k, t_k+1] . Рассм-ем все работы, лежащие над этим отрезком, нумеруем эти работы, но в 1-уя очередь нумеруются работы, которые начин-ся левее начала отрезка. Эти работы нумер-ся в порядке возраст-я розности м/д полными резервами этих работ и концом их отрезка – t_k+1, остальные нумер-ся согласно 1.2 и 1.3.

68. Принципиальная схема МОБ в СНС. МОБ – система уравнений, каждое из кот-х выражает требования баланса в разрезе каждой отрасли между производимым кол-вом прод-ции и совокупной потреб-тью в этой прод-ции.

При построении модели имеются в виду чистые отрасли, кот. Объединяют все произв-во данного продукта, независимо от ведомственной принадл-ти и форм собств-ти. Следует различать модель модель отчет-го и прогнозного (план-го) МОБ. Принцип-ой схемой МОБ произв-ва и распределения совокупного обществ-го продукта в стоимостном выражении явл. след-я таблица:

Отрасли-произв-ли	Отрасли потребители					Промежут-е потреб-е		Конечное использ-е,Y		Валовый выпуск,Х
	1	2	…	n
1	x11	x12	…	x1n			Y1		X1
2	x21	x22	…	x2n			Y2		X2
…	…	…	…	…	…		…		…
n	xn1	xn2	…	xnn			Yn		Xn
Промежут-е затраты		…	…
ВДС, Z	Z1	Z2	…	Zn
Валовые затраты,Х	X1	X2	…	Xn

X_ij ( ) – кол-во поставляемой прод-ции из i-той отрасли в j-тую отрасль; Y_i ( ) – кол-во поставляемой прод-ции из i-той отрасли для формирования j-того элемента конечного использования; Z_j ( ) – объем добавленной стоим-ти в j-той отрасли; X_i ( ) – объем валовой прод-ции i-той отрасли.

69.Рассмот-м схему МОБ в разрезе его крупных состав-х частей кот наз-ся квадрантами баланса, кот имеют экономич-ое содержание: 1-й предс-ет собой квадрат-ю матрицу порядка n, знач-ия располож-ые на пересеч-ях строк и столбцов-величин межотраслевых потоков прод-ии(пример: величина x₂ -стои-ть сред-в прои-ва, произведенных в отрасли №2 и потребляемых в качестве матер-ых затрат в отрасли №1. Во 2-ом представлена конеч-ая прод-ия всех отраслей продук-ии всех отраслей . Под конеч-й прод-ии поним-ся продук-ия выходящ из сферы продукц в область конеч-го испол-ния. В таблице этот раздел дан в виде одного столбца, а на самом деле этот столбец из множества столбцов: на личное потреб-ие насел-ия, общественное потребление, накопление, экспорт, и т.д. Сумма всех элементов 2-го хар-ет объем товаров и услуг, направ-ых из сферы произ-ва в сферу конеч-го использ-ия .В 3-ем отраж-ся структура валовой добавленной стоимостикаждой отрасли.

70. Основные соотношения, отражающие сущность МОБ. Запишем 2 соотношения, кот. является основой мат. модели МОБ:

1)если рассмотреть схему по строкам, то можно сделать вывод, что для каждой отрасли производителя вся вал. Продукция распределяется на промежуточное потребление и конечное использование. , i=1,n (1). Формула (1) представляет собой систему n-уравнений, которые называются уравнениями распределения продукции отраслей по направлениям использования.

2)если рассмотреть схему по столбцам, то для каждой отрасли потребителя вал. затраты состоят из промежуточных затрат и ВДС. , j=1,n (2). формула (2) также представляет систему n-уравнений, кот. отражают стоимостной состав продукции всех отраслей.

Просуммируем (1) и (2) по всем отраслям: , . Из последних двух соотношений видно: (3). Формула (3) показывает, что в МОБ соблюдается важнейший принцип единства материального и стоимостного состава ВВП. ВВП можно определить 3-мя методами: 1) метод по конечному использованию. Используются данные 2-ого квадранта: У= 2) финансовый метод. Используются данные 3-его квадранта: У= 3) производственный метод. Отражаются показатели 1-ого квадранта: У=

71. Мат. модель МОБ. Эк. сущность коэф-тов прямых затрат (КПЗ). Основу МОБ составляет технологическая матрица, кот. состоит из к-тов прямых затрат – мат-ных затрат на произв-во ед-цы прод-ции, кот. рассчитываются по формуле: i,j=1,n (1). КПЗ показывают какое кол-во прод-ции i-ой отрасли необходимо, если учитывать произв-во ед-цы прод-ции j-ой отрасли. Они не зависят от объема произв-ва в отрасли и явл. довольно стабильной величиной во времени. Исп-зуя ф-лу , i=1,n, можно записать в виде: Если ввести векторно-матричную запись, то последнюю формулу можно записать в виде:

Х=АХ+У – ЭММ МОБ (модель Леонтьева, модель «затраты-выпуск»).

72. Исп-ние МОБ в иссл-нии взаимосвязи отр стр-р валового выпуска и кон спроса.К-ты полн затр и их св-ва.

Исп-я формулу X=AX+B(модель Леонтьева,модель затр-выпуск)можно произ-ть след расчеты:

1)если в модели будут заданы вел-ны валов прод кажд отр,то можно опред вел-ны конечн прод кажд отр: Y=(E-A)*X,где Е-един матрица порядка n.

2)если в модели будут заданы вел-ны конеч прод,то можно найти объемы валов выпуска кажд отр: X=(E-A)^-1*Y.

Обозн (E-A)^-1 через В: (E-A)^-1=В= /IE-AI, где (E-A)^-1 – обратн матр к матр (E-A); – присоед матр к матр (E-A),эл-ты кот предст соб алгебраич дополн эл-тов транспонир матр (E-A)^т; IE-AI – определитель матр (E-A).

Эл-ты матр В наз к-тами полн матер затр,кот показыв какое кол-во прод i-ой отр нужно произвести,чтобы с учетом прям и косв затр получ единицу j-ой отр.

73. Использование МОБ в прогнозировании цен. М-ли МОБ используются при прогн-и цен. Прогноз цен на период t осуществляется на основании данных МОБ периода (t-1), на основе первого и третьего квадратов МОБ с использованием соотношения: ,j= . (1)

Обозначим индекс роста цен в i-отрасли через , тогда в табл. МОБ данные запишутся след. образом:

С учетом индекса цен ф-ла 1 перепишется в виде:

, j= - базовая балансовая стоимость для прогнозир. цен в отраслях.

18