
- •1. Понятие эконометрики. Осн-е задачи эконометрики
- •2. Понятие корреляции и регрессии. Виды регр-й и корр-ий. Задачи регр-ого и корр-ого анализа.
- •4. Метод наимен квадратов (мнк)
- •5.Коэффициент корреляции.
- •7. Анализ точности определения оценок коэффициентов регрессии
- •8. Проверка гипотез относит. Коэф-тов лин. Ур-я регрессии
- •9. Интерв. Оценки коэф-ов лин. Ур-ния регрессии
- •10. Доверительный интервал для зависимой переменной
- •14. Дисперсии и станд. Ошибки коэф-в мр
- •17. Проверка общего кач-ва уравнения множественной регрессии.
- •19. Проверка равенства двух коэффициентов детерминации
- •26 Показательная модель.
- •31.Основные проблемы, возникающие при решении задач векторной оптимизации.
- •3. Проблема определения области компромисса.
- •32. Методы решения многоцелевых задач.
- •36. Метод равных и наименьших относительных отклонений.
8. Проверка гипотез относит. Коэф-тов лин. Ур-я регрессии
При стат. анализе возник. необх-ть сравнения эмпирич.значений коэф-тов с теоретич. ожидаемыми их значениями. Такой анализ осущ-ся по схеме статистич. проверки гипотез.
Гипотеза
 ,
подлежащая проверке, наз-ся основой(нулевой).
Гипотеза
,
подлежащая проверке, наз-ся основой(нулевой).
Гипотеза
 ,
которая будет приниматься, если отклонится
наз-ся альтернативной (конкурирующей).
,
которая будет приниматься, если отклонится
наз-ся альтернативной (конкурирующей).
Для
проверки гипотезы
: =
= ;
:
;
: ≠
,строится
t-статистика
по формуле
≠
,строится
t-статистика
по формуле
 =(в0-β)/
=(в0-β)/ .
При справедливости гипотезы
она имеет распределение Стьюдента с
числом степеней свободы ν=n-2,
где
n-объем
выборки. По числу степеней свободы и
заданному ур-ню значимости α по таблицам
критич. точек нах-ся критич.значение
.
При справедливости гипотезы
она имеет распределение Стьюдента с
числом степеней свободы ν=n-2,
где
n-объем
выборки. По числу степеней свободы и
заданному ур-ню значимости α по таблицам
критич. точек нах-ся критич.значение
 Гипотеза
отклоняется,
если│
│≥
Гипотеза
отклоняется,
если│
│≥ (для
коэф-та
аналогично).
(для
коэф-та
аналогично).
На
начальном этапе статистич. анализа
более важной задачей явл-ся установление
линейн. связи между переменными X,Y.Эта
задача решается аналогично:
:
=0;
:
≠0.
 =
:
=
: ;
│
│≥
,
то гипотеза
отклоняется.
Данную гипотезу называют гипотезой о
статистич. значимости коэф-та регрессии.
Если
приним-ся,
-статистически
незначим. Чтобы определить статистич.
значимость можно не пользоваться
таблицами:
;
│
│≥
,
то гипотеза
отклоняется.
Данную гипотезу называют гипотезой о
статистич. значимости коэф-та регрессии.
Если
приним-ся,
-статистически
незначим. Чтобы определить статистич.
значимость можно не пользоваться
таблицами:
Если
│t│ 1-то
в этом случае коэф-т не может быть признан
значимым. Доверительная вероят-ть
составит меньше чем 0,7
1-то
в этом случае коэф-т не может быть признан
значимым. Доверительная вероят-ть
составит меньше чем 0,7
Если 1≤│t│ 2- то найденная оценка может рассматриваться как слабозначимая. В этом случае доверит. вероят-ть нах-ся в пределах 0,7 и 0,95.
Если 2≤│t│ 3- то в этом случае говорят о сильной линейной зависимости X и Y.Доверительная вероят-ть от 0,95 до 0,99.
Если
│t│ 3-очень
сильная линейная зависимость.
3-очень
сильная линейная зависимость.
9. Интерв. Оценки коэф-ов лин. Ур-ния регрессии
Рассм-им
t-статистику:

Чтоб
построить 100(1-
 )доверит.интервал
по треб-му уровню знач-ти
и числу степени свободы,опред-ся критич.
знач-е:
)доверит.интервал
по треб-му уровню знач-ти
и числу степени свободы,опред-ся критич.
знач-е:
 ,
n-2,
кот. удовл-ет след. усл-ю:
,
n-2,
кот. удовл-ет след. усл-ю:

Подставим и получим.


Выраж-ие в скобках и опред-ет доверит. интервал
10. Доверительный интервал для зависимой переменной
Одной
из задач эк. моделир-я является прогнозир-е
зависимой переменной при определённых
знач-х независимой переменной. Пусть
построено ур-е регрессии:

Необходимо
на осн. данного ур-я предсказать условное
мат. M
(Y/xp)
переменной Y
при Х=хр.
Значение
 является оценкой M
(Y/xp).
является оценкой M
(Y/xp).
Возникает
вопрос как сильно может отклониться
модельное значение
 от соответствующего условного мат.
ожидания M
(Y/xp).
Покажем, что случ. величина
от соответствующего условного мат.
ожидания M
(Y/xp).
Покажем, что случ. величина
 имеет нормальное распределение, для
этого исп-ем формулы для ci
и di.
имеет нормальное распределение, для
этого исп-ем формулы для ci
и di.

Следовательно случ. величина явл. линейной комбинацией нормальных случ. величин, значит и сама имеет норм. распределение. Найдём мат. ожидание и дисперсию данной случ. величины.





Поскольку
 по выборке определена быть не может, то
вместо её подставим несмещённую оценку:
по выборке определена быть не может, то
вместо её подставим несмещённую оценку:
 , тогда получим выборочную исправленную
дисперсию величины
, тогда получим выборочную исправленную
дисперсию величины
 .
.

В
дельнейшем будем исп-ть случ. величину
 ,
которое имеет распределение t-стьюдента
с числом степеней свободы ν=n-2.
,
которое имеет распределение t-стьюдента
с числом степеней свободы ν=n-2.
По
заданному уравнению значимости α и
числу степеней свободы определяем
критич. точку
 ,n-2
, кот. удовлетворяет след. условию
,n-2
, кот. удовлетворяет след. условию
 .
.
Подставим
значение вместо t→
 ,n-2<
,n-2< ,n-2
=
,n-2
=

Выражение
в скобках и определяет доверительный
интервал для условного мат. ожидания
 .
.
11.Проверка
общего кач-ва ур-ния регрессии.
Мерой
общего кач-ва ур-ния регрессии ,т.е.
соотв-ия ур-ния регрессии к стат. данным
явл. коэф-т детерминации (R2),кот.
определяется по след. формуле:
R2=1-( ei2/
(yi
-y¯)2).
Выясним смысл коэф-тов детерминации:
как известно, реальные значения зависимой
переменной отлич. от модельных значений
на величину ei
: yi=yi^+
ei
, i=1,n.
Последнее соотнош-е можно переписать
в виде:yi-y^=(yi^-y¯)+(yi-yi^),
где yi-
y¯
- отклонение i-ой
наблю-ой точки от среднего значения;
yi^-y¯
- - отклонение i-ой
наблю-ой точки на линии регрессии от
среднего значения; yi-yi^
- отклонение i-ой
наблю-ой точки от модельного знач-я.
ei2/
(yi
-y¯)2).
Выясним смысл коэф-тов детерминации:
как известно, реальные значения зависимой
переменной отлич. от модельных значений
на величину ei
: yi=yi^+
ei
, i=1,n.
Последнее соотнош-е можно переписать
в виде:yi-y^=(yi^-y¯)+(yi-yi^),
где yi-
y¯
- отклонение i-ой
наблю-ой точки от среднего значения;
yi^-y¯
- - отклонение i-ой
наблю-ой точки на линии регрессии от
среднего значения; yi-yi^
- отклонение i-ой
наблю-ой точки от модельного знач-я.
Возведем обе части в квадрат и просуммируем по всем n: (yi-y¯)2= (yi^-y¯)2+2* (yi^-y¯)2*ei+ (yi-yi^)2.
(yi-y¯)2 –полная сумма квадратов ( меру разброса зависимой переменной относительно среднего значения).
(yi^-y¯)2 –обьясненная сумма квадратов (мера разброса, кот. объясняется с помощью регрессии).
(yi-yi^)2 –необъясненная сумма квадратов.
Разделим обе части последнего выражения на левую часть, получим:
1=( (yi^-y¯)2/ (yi-y¯)2)+( ei2/ (yi-y¯)2). Введем обозначения: R2= (yi^-y¯)2/ (yi-y¯)2, тогда получим исходную формулу. Коэф-т детерминации (R2) определяет долю разброса зависимой переменной, объяснимую ур-нием регрессии. 0≤R2≤1, чем ближе R2 к единице, тем лучше кач-во постр-ой регрессии. Можно показать, что R2=ryx2. Судить о кач-ве ур-ния регрессии можно и по средней ошибке аппроксимации, котор. опред-ся по формуле: A¯=1/n* Iyi-yi^/yiI*100%, если A¯≤10%, то построенное ур-ние регрессии качественно.
12.
На
любой экон. показатель чаще всего оказ.
влияние не один, а неск. факторов. В этом
сл. вместо парной регрессии рассм. мн.
регрессия. M(Y/x1,
x2,
..., xm)=f(x1,
x2,
…, xm).
Ур-е мн. регр. в общем виде Y=f(β,
x)+ε,
где β=
β0,
β1,
…,
βm
- вектор теоретических коэфф-в, кот.
нужно опред. X=(X1,
X2,
…, Xm)
– в-р незав. перем. Теоретическое лин.
ур-е множ. регр-и: Y
= β0+
β1X1+
β2X2+…+
βmXm+ε,
или в каждом конктреном случае yi=
β0+
β1xi1+
β2xi2+…+
βmxim+εi,
i= .
Число степеней свободы для множ. лин.
регр-и равно ν=n-m-1.
Если n>m+1,
то возник. необх-ть оценивания теоретич.
коэфф. регр-и. Как и в случае парной
регр-и мы будем использ. метод наим.
квадратов. Так и для парной регр-и должны
вып-ся предпосылки Гаусса-Маркова. Но
для множ. регр-и очень существ-ми явл.
еще 2 предпосылки. Отсутствие
мультиколлинеарности, т.е. м-ду незав.
перем-ми должна отсутств. сильная лин.
зав-ть. Случ. отклон-е εi,
i=
должны иметь норм. распределение εi
~
N(0,
δ2).
Как и в случ. парной регр-и истинные
знач-я коэфф-в по выборке опред-ть
невозможно, поэтому строится эмпирич.
ур-е регр-и.
.
Число степеней свободы для множ. лин.
регр-и равно ν=n-m-1.
Если n>m+1,
то возник. необх-ть оценивания теоретич.
коэфф. регр-и. Как и в случае парной
регр-и мы будем использ. метод наим.
квадратов. Так и для парной регр-и должны
вып-ся предпосылки Гаусса-Маркова. Но
для множ. регр-и очень существ-ми явл.
еще 2 предпосылки. Отсутствие
мультиколлинеарности, т.е. м-ду незав.
перем-ми должна отсутств. сильная лин.
зав-ть. Случ. отклон-е εi,
i=
должны иметь норм. распределение εi
~
N(0,
δ2).
Как и в случ. парной регр-и истинные
знач-я коэфф-в по выборке опред-ть
невозможно, поэтому строится эмпирич.
ур-е регр-и.
 =b0+b1x1+…+bmxm.
Для кажд. наблюд-я мы получим yi=
=b0+b1x1+…+bmxm.
Для кажд. наблюд-я мы получим yi= +ei
i=
.
Для нахожд-я оценок b0,
b1,
…, bm
исп-ся ф-ла Q(b0,
b1,
…, bm)=
+ei
i=
.
Для нахожд-я оценок b0,
b1,
…, bm
исп-ся ф-ла Q(b0,
b1,
…, bm)=
 min.
Данн. ф-я явл. квадратичной. Необх. усл-ем
сущ-я минимума явл. =0 всех ее частичных
производных
min.
Данн. ф-я явл. квадратичной. Необх. усл-ем
сущ-я минимума явл. =0 всех ее частичных
производных
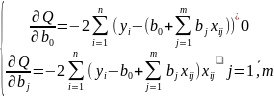
13. Расчет коэффициентов множ. регр. Представим данные набл-ий и соотв-ие коэф-ты в матр. форме:
x11
x12 ... x1n
x21
x22 ... x2n
… x1m
x2m
…xmn ............................... 1 xn1 xn2 ...
xnm

 y1
b0 e1
y1
b0 e1
y2 b1 e2
Y= y3 , X= , B= ... , e = ...
...
yn bm en
Ф-цию
Q
= в матр. форме можно предст. как произв-е
в матр. форме можно предст. как произв-е
 - вектор строки на вектор-столбец е. А в
свою очередь вектор-столбец е можно
записать в виде: е= У-ХВ.
- вектор строки на вектор-столбец е. А в
свою очередь вектор-столбец е можно
записать в виде: е= У-ХВ.
Тогда их ф-цию Q запишем в виде: Q= е=(У-ХВ)Т(У-ХВ)=УТУ-ВТХТУ-УТ ХВ+ВТХТ ХВ=УТУ-2 ВТХТУ+ ВТХТ ХВ
Мат-ки док-но, что в.-столбец частных производных ф-ции Q по оцениваемым парам-рам имеет вид:
 .
Приравняем
.
Приравняем
 =0,
получим форм-лу для вычисл-я оц-к множ.
лин. регр.:
=0,
получим форм-лу для вычисл-я оц-к множ.
лин. регр.:
( )В=ХТУ
=> В=(
)-1
ХТУ.
)В=ХТУ
=> В=(
)-1
ХТУ.
