11.4 Задача Коши для дифференцмального уравнения

Задача Коши – это задача нахождения частного решения дифференциального уравнения, удовлетворяющего заданным начальным условиям  , где   - числа

11.5 дифференциальное уравнение с разделяющимися пепеменными.\

Определение и способ решения

Пусть   — некоторая функция,   — ее производная. Для удобства будем записывать производную виде  , имеющем смысл отношения бесконечно малых приращений — дифференциалов. Дифференциал   — приращение значения переменной в окрестности  , стремящееся к нулю. Дифференциал функции   — малое приращение функции,  . Пусть   и   — некоторые функции от   и  . Рассмотрим уравнение

.

Уравнение такого вида называется обыкновенным дифференциальным уравнением сразделяющимися переменными. Умножим его на  :

.

Последнее равенство означает, что малые приращения левой и правой частей равны. Поэтому их суммы также равны. Предположим что при     и возьмем интегралы от левой и правой частей. Пределы интегрирования — от   до   для левой части и от  для   для правой части уравнения:

.

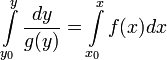Решая получившееся в результате интегрирования алгебраическое уравнение, мы можем выразить  .

Значения   и   называются начальными условиями. В случае других начальных условий решение уравнения будет отличаться на постоянную. Поэтому, если начальные условия не даны, можно взять первообразные левой и правой частей и прибавить к ним константу. Используя неопределенный интеграл — обозначение множества первообразных —  , где   —первообразная  ,   — произвольная постоянная, запишем это в виде

.

Следует отметить, что у дифференциального уравнения с разделяющимися переменными могут существовать так называемые нулевые решения — постоянные  , удовлетворяющие уравнению  . При них равны нулю как правая, так и левая части дифференциального уравнения (поскольку производная константы равна нулю).

Пример 1

Решить дифференциальное уравнение  .

Разделим переменные:

.

Т. к. начальные условия не заданы, возьмем неопределенный интеграл от обеих частей уравнения:

,

.

Осталось лишь выразить   через  :

.

Найдем также нулевые решения:

.

Ответ:  .

11.6 Понятие однородной функции двух переменных и однородного дифференциального уравнения.

Однородное дифференциальное уравнение может быть записано в виде

или

где   ,   - однородные функции одной и той же степени, т.е. для некоторого натурального числа   и для произвольного   справедливы равенства

Для решения однородного дифференциального уравнения необходимо сделать замену переменных   , которая сводит однородное дифференциальное уравнение кдифференциальному уравнению с разделяющимися переменными.

Пример 1 - решить дифференциальное уравнение

ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ

43.1. Основные понятия

Пусть задано множество D упорядоченных пар чисел (х;у). Соответствие ƒ, которое каждой паре чисел (х; у) є D сопоставляет одно и только одно число z є R, называется функцией двух переменных, определенной на множестве D со значениями в Е, и записывается в виде z = ƒ(х;у) или ƒ : D → R При этом х и у называются независимыми переменными (аргументами), а z — зависимой переменной (функцией).

Множество D = D(f) называется областью определения функции. Множество значений, принимаемых z в области определения, называется областью изменения этой функции, обозначается E(f) или Е.

Примером функции двух переменных может служить площадь S прямоугольника со сторонами, длины которых равны х и у: S = ху. Областью определения этой функции является множество {(х;у) | х > 0, у > 0}.

Функцию z = ƒ(х;у), где (х;у) є D можно понимать (рассматривать) как функцию точки М(х;у) координатной плоскости Оху. В частности, областью определения может быть вся плоскость или ее часть, ограниченная некоторыми линиями. Линию, ограничивающую область, называют границей области. Точки области, не лежащие на границе, называются внутренними. Область, состоящая из одних внутренних точек, называется открытой. Область с присоединенной к ней границей называется замкнутой, обозначается D. Примером замкнутой области является круг с окружностью.

Значение функции z = ƒ(х;у) в точке М0(х0;у0) обозначают z0=ƒ(хо;уо) или z0=ƒ(М0) и называют частным значением функции.

Ф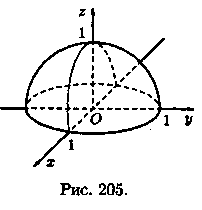 ункция двух независимых переменных допускает геометрическое истолкование. Каждой точке М0(х₀; у₀) области D в системе координат Oxyz соответствует точка M(x₀;y₀;z₀), где z₀ = ƒ(х_о;у_о) — аппликата точки М. Совокупность всех таких точек представляет собой некоторую поверхность, которая и будет геометрически изображать данную функцию z=ƒ(x;у).

Например, функция имеет областью определения круг х² + у² ≤ 1 и изображается верхней полусферой с центром в точке O(0;0;0) и радиусом R = 1 (см. рис. 205).

Функция двух переменных, как и функция одной переменной, может быть задана разными способами: таблицей, аналитически, графиком. Будем пользоваться, как правило, аналитическим способом: когда функция задается с помощью формулы.