
- •Метод Ейлера для розв’язування задач Коші
- •Вдосконалений метод Ейлера
- •Метод Ейлера-Коші
- •Збіжність методу Ейлера
- •Методи Рунге-Кутта
- •Метод Рунга-Кута 3-го порядку
- •Метод Рунга-Кута 4-го порядку
- •Методи розв’язання лінійних рівнянь та їх систем
- •Метод Ньютона для відшукання верхньої межі коренів
- •Метод Штурма
- •Метод простої ітерації
- •Метод хорд
- •Метод Ньютона
- •Комбіновий метод хорд і дотичних
- •Метод січних
- •Метод поділу відрізка пополам
- •Збіжність методу простої ітерації
- •Збіжність методу Ньютона
- •Ітераційні методи для систем нелінійних рівнянь
- •Метод релаксації
- •Метод Пікара
- •Метод Ньютона
- •Модифікований метод Ньютона
Чисельні методи розв’язування задачі Коші для звичайних диференціальних рівнянь

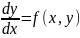
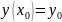
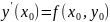
Р озв’язком
задачі коші є інтегральна крива, яка
проходить через задану точку
озв’язком
задачі коші є інтегральна крива, яка
проходить через задану точку
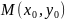 .
Припускаємо що
.
Припускаємо що
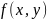 є неперервною по змінних x
і y
в деякій області
є неперервною по змінних x
і y
в деякій області
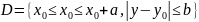 .
Із неперервності функції
буде випливати її обмеженість, тобто
.
Із неперервності функції
буде випливати її обмеженість, тобто
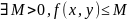 .
А також
задовільнює умову Ліпшеца по змінній
.
А також
задовільнює умову Ліпшеца по змінній
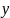 .
.
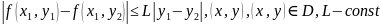
Якщо виконується вказані припущення то розвязок існує і він єдиний. При подальшому припускатимемо, що розвязок задачі Кші існує і він єдиний і задовольняє певним умовам гладкості.
Метод Ейлера для розв’язування задач Коші
Нехай потрібно розв’язати задачу (1-2) тоді при чисельному розв’язанні задачі (1) задача ставитиметься в наступному вигляді.
В
точцах
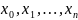 потрібно знайти наближення
потрібно знайти наближення
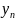 для точного значення
для точного значення
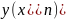 , де
-
наближення,
– точне
, де
-
наближення,
– точне
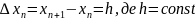 -крок
сітки
-крок
сітки
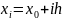 .
.
Проінтегруємо ліву і праву частину рівняння (1) на кожному із проміжка
[ ]
:
]
:
 .
.
При
дуже малому кроці сітки
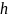 вважатимемо значення функції
на кожному із проміжків сталою тоді (4)
запишемо як
вважатимемо значення функції
на кожному із проміжків сталою тоді (4)
запишемо як
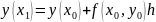
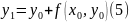
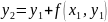
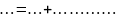
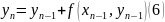
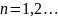 (6) – метод Ейлора
(6) – метод Ейлора
Ми замінюємо інтегральну
криву прямолінійним відрізком який
виходить із точки
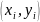 .
Геометрично метод полягає в заміні
інтегральної кривої ламаною і кожна
ланка цієї ламаної є прямолінійна і
вона виходить з точки
з кутовим коефіцієнтом
.
Геометрично метод полягає в заміні
інтегральної кривої ламаною і кожна
ланка цієї ламаної є прямолінійна і
вона виходить з точки
з кутовим коефіцієнтом
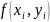 .
Таку ламану ще називають «Ламаною
Ейлера». Недоліком є мала точність і
систематичне накопичення похибки.
.
Таку ламану ще називають «Ламаною
Ейлера». Недоліком є мала точність і
систематичне накопичення похибки.
Вдосконалений метод Ейлера
Для побудови даного методу ми будемо обчислювати значення в деякій проміжній точці
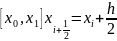
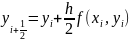
Знайдемо значення функції
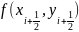
Тоді удосконалений метод Ейлера буде виглядати
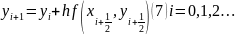
Удосконалений
метод Ейлера полягає в побудові Ламаної
Ейлера, де на кожній ділянці [ ]
ми заміняємо прямолінійним відрізком,
який виходить із точки
з кутовим коефіцієнтом
]
ми заміняємо прямолінійним відрізком,
який виходить із точки
з кутовим коефіцієнтом
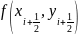
Метод Ейлера-Коші
В
методі Ейлера-Коші замість
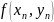 ми
будемо обраховувати середнє арифметичне
ми
будемо обраховувати середнє арифметичне
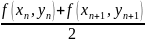
тоді одержимо формулу
 метод Ейлера-Коші
метод Ейлера-Коші
Збіжність методу Ейлера
При
розгляді чисельних методів головним
питанням є питання збіжності. Стосовно
різницевих методів, до яких відноситься
метод Ейлера, важливим є поняття збіжності
при
 .
Для доведення збіжності ми будуємо
послідовність сіток
.
Для доведення збіжності ми будуємо
послідовність сіток
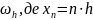 таких що при
таких що при
 .
Будемо говорити що метод Ейлера збігається
в точці
.
Будемо говорити що метод Ейлера збігається
в точці
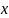 ,
якщо
,
якщо

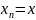 тоді ж метод збігається на проміжку,
якщо він збігається в кожній точці цього
проміжку.
тоді ж метод збігається на проміжку,
якщо він збігається в кожній точці цього
проміжку.
Кажуть,
що метод має
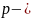 тий
порядок точності, якщо
тий
порядок точності, якщо
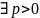 ,
що виконується
,
що виконується
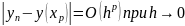 .
.
Будемо
говорити, що різницевий метод апроксимує
дане диференціальне рівняння, якщо
похибка прямує до нуля при
.,також
метод має
 -ий
порядок апроксимації якщо похибка
нескінченно мала
того
порядку.
-ий
порядок апроксимації якщо похибка
нескінченно мала
того
порядку.
Знайдемо оцінку похибки.
Припустимо
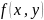 є неперервною в області
є неперервною в області
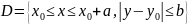
і
задовольняє умову Ліпшеца з сталою
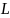 .
.
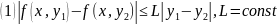
Також виконується
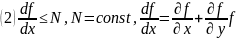
тоді
розглянемо диференціальне рівняння
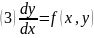 тоді звичайний метод Ейлера
буде виглядати:
тоді звичайний метод Ейлера
буде виглядати:
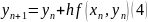
Тоді
позначимо похибку
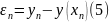 це похибка наближення
до точного значення
це похибка наближення
до точного значення
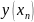 .
Тоді за допомогою рівнянь виду (5)
можемо записати рівняння для приросту
похибки для
.
Тоді за допомогою рівнянь виду (5)
можемо записати рівняння для приросту
похибки для
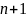 рівняння
рівняння

У рівнянні (6) враховуючи (4), можемо продовжити
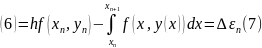
У (7) про інтегруємо другий доданок по частинах
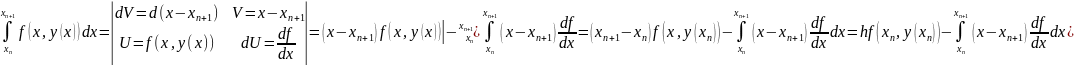
Підставимо одержаний вираз у (7) тоді

Врахувавши обмеження (2), а також умову Ліпшеца(1)
 \
\
Врахувавши (5):
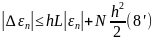
Розглянемо рівність (6):
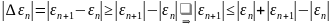
Врахувавши (8’)
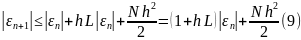
Таким
чином (9) представляє собою рекурентну
оцінку похибки на
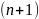 кроці через
кроці через
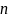 -тий
крок. Розглянемо оцінку на
–товім
кроці.
-тий
крок. Розглянемо оцінку на
–товім
кроці.
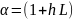
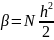
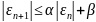
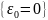
Тоді можемо записати

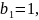


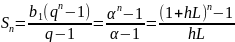
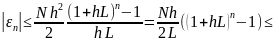
Використаємо рівність
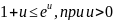
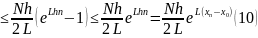
Ми одержимо похибку
 де
де
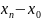 -величина
проміжку а.
-величина
проміжку а.
Як бачимо з формули оцінки похибки, Метод Ейлора має 1-й порядок апроксимації із зменшенням кроку похибка зменшується. Тому можемо зробити висновок, що на довільнім скінченнім проміжку при метод є збіжний, але недоліком цього методу є повільна збіжність.
Дослідимо метод Ейлера на стійкість.
Не завжди початкове наближення
буде одержане точно, тобто замість
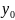 ми будемо враховувати
ми будемо враховувати
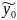 .
.
 -
абсолютна похибка між точними і
наближеними значеннями.
-
абсолютна похибка між точними і
наближеними значеннями.
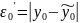 ,
тоді врахувавши метод Ейлера (4)
можемо записати
,
тоді врахувавши метод Ейлера (4)
можемо записати

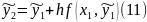

Знайдемо абсолютну похибку враховуючи що функція задовольняє умову Ліпшица
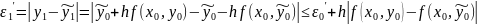

…. …. ….
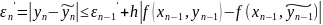
Тоді

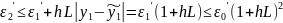
…. .… .….

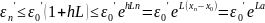
Із останньої нерівності випливає що похибка початкових даних не накопичується, тобто метод Ейлера має обчислювальну стійкість
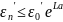
Можемо сказати що похибка початкових даних не накопичується в методі Ейлера і метод має обчислювальну стійкість.
