
- •2) A) Естественный способ задания движения.
- •3) А) Скорость точки при векторном способе задания движения
- •5 ) Дифференцирование единичного вектора
- •7) А) Ускорение точки
- •8) Поступательное движение твердого тела.
- •9) Вращение твёрдого тела вокруг неподвижной оси
- •10) Скорости и ускорения точек тела при вращении.
- •11) Плоское движение твердого тела
- •12) Теорема о проекциях скоростей двух точек тела.
- •13) Мгновенный центр скоростей
- •15) Сложение ускорений в общем случае плоского движения
- •19) Угловая скорость и угловое ускорение при сферическом движении твердого тела
- •20) Разложение движения свободного тела на поступательное и вращательное.
- •21) Относительное, переносное и абсолютное движение точки.
- •22) Teopeмa сложения скоростей.
- •23) Сложение ускорений в общем случае переносного движения
22) Teopeмa сложения скоростей.
П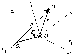 усть
система отсчета O1x1y1z1
- неподвижная, а система отсчета Oxyz
- подвижная.
Движение точки относительно основной
неподвижной системы отсчета O1x1y1z1
называется
абсолютным.
Движение точки относительно подвижной
системы отсчета Oxyz
называется относительным.
Переносным
движением точки называется движение,
которое она совершает вместе с подвижной
системой отсчета, как точка, жестко
скрепленная с этой системой в
рассматриваемый момент времени.
Относительные скорость и ускорение
обозначают
и
усть
система отсчета O1x1y1z1
- неподвижная, а система отсчета Oxyz
- подвижная.
Движение точки относительно основной
неподвижной системы отсчета O1x1y1z1
называется
абсолютным.
Движение точки относительно подвижной
системы отсчета Oxyz
называется относительным.
Переносным
движением точки называется движение,
которое она совершает вместе с подвижной
системой отсчета, как точка, жестко
скрепленная с этой системой в
рассматриваемый момент времени.
Относительные скорость и ускорение
обозначают
и
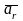 ,
переносные -
,
переносные -
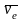 и
и
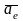 ,
а абсолютные -
и
.
,
а абсолютные -
и
.
Движение
подвижной системы отсчета относительно
неподвижной можно охарактеризовать
скоростью ее поступательного движения
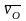 ,
например вместе с точкой О,
и вектором угловой скорости
,
например вместе с точкой О,
и вектором угловой скорости
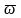 ее вращения вокруг О.
ее вращения вокруг О.
Теорема.
Скорость абсолютного движения точки
равна векторной сумме переносной и
относительной скоростей. 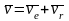
Доказательство.
Рассмотрим движение точки
.
Положение точки
относительно
неподвижной системы отсчета определяется
вектором
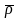 ,
а относительно подвижной вектором
.
Положение точки
,
а относительно подвижной вектором
.
Положение точки
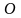 относительно неподвижной системы
отсчета определяется вектором
относительно неподвижной системы
отсчета определяется вектором
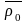 .
Для любого момента времени выполняется
тождество
.
Для любого момента времени выполняется
тождество 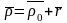 .
.
Продифференцируем его по времени (вычислим производные в неподвижной системе отсчета) и получим
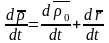 (9-5)
(9-5)
По
определению, 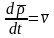 - абсолютная скорость точки
,
- абсолютная скорость точки
,
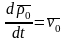 - абсолютная скорость точки
.
Для вычисления
- абсолютная скорость точки
.
Для вычисления
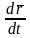 применим формулу Бура. Имеем
.
Относительная производная
- является относительной скоростью
точки
по отношению к неподвижной системе
отсчета, а
- угловая скорость вращения подвижной
системы отсчета.
применим формулу Бура. Имеем
.
Относительная производная
- является относительной скоростью
точки
по отношению к неподвижной системе
отсчета, а
- угловая скорость вращения подвижной
системы отсчета.
Таким образом из (9-5) получаем

Скорость
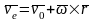
является скоростью точки свободного твердого тела, скрепленного с подвижной системой координат, с которой в данный момент совпадает точка в движении тела относительно неподвижной системы отсчета. Это есть переносная скорость точки .
Окончательно получаем
,
что и требовалось доказать.
23) Сложение ускорений в общем случае переносного движения
Теорема. (кинематическая теорема Колиолиса) Абсолютное ускорение точки является векторной суммой трех ускорений - переносного, относительного и Кориолиса.
Доказательство. Абсолютное ускорение точки определим вычислением полной производной по времени от абсолютной скорости.
Для производных от векторов и применим формулу Бура. Получим
Учитывая, что , , , ,
получим для абсолютного ускорения
В этой формуле первые три слагаемых являются переносным ускорением для точки . Последнее слагаемое называется ускорением Кориолиса (иногда его называют добавочным или поворотным ускорением) и обозначается .
В итоге формула (9-8) принимает вид
,
что и требовалось доказать.
24-25) Сложение вращений тела вокруг двух осей
На
рис. 54 изображено тело, которое совершает
сложное движение – вращение вокруг
оси, которая сама вращается вокруг
другой, неподвижной оси. Естественно,
первое вращение следует назвать
относительным движением тела, второе
– переносным, а соответствующие оси
обозначить ![]() и
и ![]() .
.

Рис.54
Абсолютным
движением будет вращение вокруг точки
пересечения осей О.
(Еcли
тело имеет больший размер, то
его точка, совпадающая с О,
все время будет неподвижной). Угловые
скорости переносного вращения и
относительного вращения
изображается векторами ![]() и
и ![]() ,
отложенными из неподвижной точки О,
точки пересечения осей, по соответствующим
осям.
,
отложенными из неподвижной точки О,
точки пересечения осей, по соответствующим
осям.
Найдем
абсолютную скорость какой-нибудь
точки М тела,
положение которой
определяется радиусом-вектором ![]() (рис.54).
(рис.54).
Как
известно, она складывается из двух
скоростей, относительной и
переносной: ![]() .
Но относительное движение
точки (используя правило
остановки), есть вращение с угловой
скоростью
вокруг оси
,
определяется радиусом-вектором
.
Поэтому,
.
Но относительное движение
точки (используя правило
остановки), есть вращение с угловой
скоростью
вокруг оси
,
определяется радиусом-вектором
.
Поэтому, ![]() .
.
|
Переносное
движение точки в данный момент времени,
опять используя правило остановки,
тоже есть вращение, но вокруг
оси
с
угловой скоростью
и
будет определяться тем же радиусом-вектором
.
Поэтому и переносная скорость ![]() .
.
Абсолютная
же скорость, скорость при вращении
вокруг неподвижной точки О,
при сферическом движении, определяется аналогично ![]() , где
, где ![]() -
абсолютная угловая скорость, направленная
по мгновенной оси вращения Р.
-
абсолютная угловая скорость, направленная
по мгновенной оси вращения Р.
По формуле сложения скоростей получим: ![]() или
или ![]() .
.
Отсюда ![]()
То есть мгновенная угловая скорость, угловая скорость абсолютного движения, есть векторная сумма угловых скоростей переносного и относительного движений. А мгновенная ось вращения P, направленная по вектору , совпадает с диагональю параллелограмма, построенного на векторах и (рис.54).
Частные случаи:
1. Оси вращения и параллельны, направления вращений одинаковы (рис. 55).
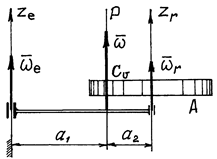
Рис.55
Так
как векторы
и
параллельны
и направлены в одну сторону, то
абсолютная угловая скорость по величине
равна сумме их модулей ![]() и
вектор ее направлен в туже
сторону. Мгновенная ось вращения Р делит
расстояние между осями на части
обратно пропорциональные
и
вектор ее направлен в туже
сторону. Мгновенная ось вращения Р делит
расстояние между осями на части
обратно пропорциональные ![]() и
и ![]() :
:
![]() . (Аналогично равнодействующей
параллельных сил).
. (Аналогично равнодействующей
параллельных сил).
В этом
частном случае тело А совершает
плоскопараллельное движение. Мгновенный
центр скоростей ![]() находится
на оси Р.
находится
на оси Р.
2. Оси вращения параллельны, направления вращений противоположны (рис.56).
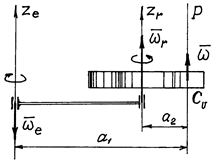
Рис.56
В этом случае ![]() (при
(при ![]() ). Мгновенная ось вращения и мгновенный центр скоростей находятся
за вектором большей угловой скорости
на расстояниях таких, что
(опять
по аналогии определения
равнодействующей параллельных
сил).
). Мгновенная ось вращения и мгновенный центр скоростей находятся
за вектором большей угловой скорости
на расстояниях таких, что
(опять
по аналогии определения
равнодействующей параллельных
сил).
3. Оси вращения параллельны, направления вращений противоположны и угловые скорости равны.
Угловая
скорость абсолютного движения ![]() и,
следовательно,
тело совершает поступательное движение. Этот случай называется парой
вращений, по
аналогии с парой сил.
и,
следовательно,
тело совершает поступательное движение. Этот случай называется парой
вращений, по
аналогии с парой сил.
26) Сложение поступательного и вращательного движений. Винтовое движение.
Если
сложное движение тела слагается из
вращательного вокруг оси Аа с
угловой скоростью ![]() и
поступательного со скоростью
и
поступательного со скоростью ![]() ,
направленной параллельно оси Аа (рис.63),
то такое движение тела называется
винтовым. Ось Аа называют
осью винта. Когда векторы
и
направлены
в одну сторону, то при принятом нами
правиле изображения
,
направленной параллельно оси Аа (рис.63),
то такое движение тела называется
винтовым. Ось Аа называют
осью винта. Когда векторы
и
направлены
в одну сторону, то при принятом нами
правиле изображения ![]() винт
будет правым; если в разные стороны, -
левым.
винт
будет правым; если в разные стороны, -
левым.
Р асстояние,
проходимое за время одного оборота
любой точкой тела, лежащей на оси винта,
называется шагом h винта.
Если величины
и
постоянны,
то шаг винта также будет постоянным.
Обозначая время одного оборота через Т,
получаем в этом случае
асстояние,
проходимое за время одного оборота
любой точкой тела, лежащей на оси винта,
называется шагом h винта.
Если величины
и
постоянны,
то шаг винта также будет постоянным.
Обозначая время одного оборота через Т,
получаем в этом случае ![]() и
и ![]() ,
откуда
,
откуда ![]() .
.
При
постоянном шаге любая точка М тела,
не лежащая на оси винта, описывает
винтовую линию. Скорость точки М,
находящейся от оси винта на расстоянии ![]() ,
слагается из поступательной скорости
и
перпендикулярной ей скорости, получаемой
во вращательном движении, которая
численно равна
,
слагается из поступательной скорости
и
перпендикулярной ей скорости, получаемой
во вращательном движении, которая
численно равна ![]() .
Следовательно,
.
Следовательно,
![]() .
.
Направлена
скорость ![]() по
касательной к винтовой линии. Если
цилиндрическую поверхность, по которой
движется точка М,
разрезать вдоль образующей и развернуть,
то винтовые линии, обратятся впрямые,
наклоненные к основанию цилиндра под
углом
по
касательной к винтовой линии. Если
цилиндрическую поверхность, по которой
движется точка М,
разрезать вдоль образующей и развернуть,
то винтовые линии, обратятся впрямые,
наклоненные к основанию цилиндра под
углом ![]() .
.
