12) Теорема о проекциях скоростей двух точек тела.

Определение скоростей точек плоской фигуры (или тела, дви­жущегося плоскопараллельно) связано обычно с довольно сложными расчетами. Однако можно получить ряд других, практически более удобных и простых мето­дов определения скоростей точек фигуры (или тела).

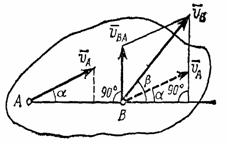
Один из таких методов дает тео­рема: проекции скоростей двух точек твердого тела на ось, проходящую через эти точки, равны друг другу. Рассмотрим какие-нибудь две точки А и В плоской фигуры (или тела). Принимая точку А за полюс (рис.32), получаем  . Отсюда, проектируя обе части равенства на ось, направленную по АВ, и учитывая, что вектор   перпендику­лярен АВ, находим

и теорема доказана.

13) Мгновенный центр скоростей

Мгновенным центром скоростей называется точка плоской фигуры, скорость которой в данный момент времени равна нулю.

Теорема. В каждый момент времени при плоском движении фигуры в ее плоскости при (непоступательное движение), имеется один единственный центр скоростей.

Для доказательства достаточно указать способ нахождения мгновенного центра скоростей, если известны скорость какой-либо точки О плоской фигуры и ее угловая скорость в рассматриваемый момент времени.

Р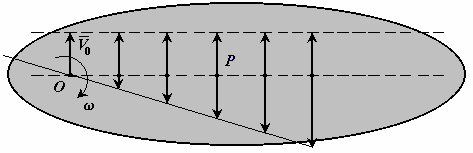 ис. 6-6

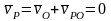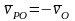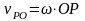, , , следовательно .

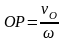Мгновенный центр скоростей находится на перпендикуляре к скорости , проведенном из точки О, на расстоянии .

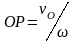Мгновенный центр скоростей это единственная точка плоской фигуры для данного момента времени. В другой момент времени мгновенным центром скоростей будет уже другая точка.

Возьмем точку Р за полюс

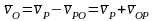
Так как 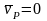, то 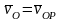. Аналогичный результат получается для любой другой точки плоской фигуры.

.

.

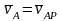
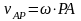
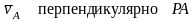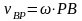
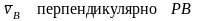Скорости точек плоской фигуры определяются в данный момент так, как если бы движение фигуры было вращением вокруг мгновенного центра скоростей.

Скорости точек плоской фигуры пропорциональны их расстояниям до мгновенного центра скоростей.

14)  При движении плоской фигуры м.ц.с. непрерывно изменяет свое положение. Геометрическое место м.ц.с., отмеченных на неподвижной плоскости, называется неподвижной центроидой. Геометрическое место м.ц.с., отмеченных на плоскости фигуры, назыв.подвижной центроидой (колесо катится по прямой: неподвижная центроида – прямая, подвижная – окружность). При движении плоской фигуры подвижная центроида катится без скольжения по неподвижной центроиде (теорема Пуансо).

15) Сложение ускорений в общем случае плоского движения

Теорема. (кинематическая теорема Колиолиса) Абсолютное ускорение точки является векторной суммой трех ускорений - переносного, относительного и Кориолиса.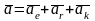

Доказательство. Абсолютное ускорение точки 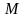определим вычислением полной производной по времени от абсолютной скорости.

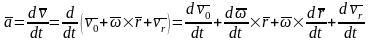
Для производных от векторов и 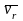применим формулу Бура. Получим

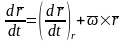
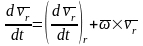
Учитывая, что , , , ,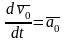

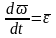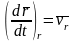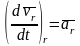получим для абсолютного ускорения

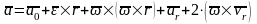
В этой формуле первые три слагаемых являются переносным ускорением для точки 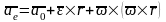. Последнее слагаемое называется ускорением Кориолиса (иногда его называют добавочным или поворотным ускорением) и обозначается .

В итоге формула (9-8) принимает вид

,

что и требовалось доказать.

16) Мгнове́нный центр ускоре́ний — при непоступательном движении точка, находящаяся в плоскости движения тела, ускорение которой в данный момент времени равно нулю.

Положение мгновенного центра ускорений в общем случае не совпадает с положением мгновенного центра скоростей. Однако в некоторых случаях, например, при чистовращательном движении, положение этих двух точек может совпадать.

17)

Для того, чтобы определить положение мгновенного центра ускорений, необходимо к векторам ускорений двух различных точек тела провести прямые под равными углами  . В точке пересечения проведённых прямых и будет находиться мгновенный центр ускорений. Угол   должен удовлетворять равенству:

где  — угловое ускорение тела;  — угловая скорость тела.

18) Сферическое движение (движение твёрдого тела вокруг неподвижной точки) — движение абсолютно твёрдого тела, при котором оно имеет одну неподвижную точку.

При движении вокруг неподвижной точки О каждая из точек твёрдого тела описывает в пространстве сферическую поверхность, центром которой является точка О.

При описании законов сферического движения принято пользоваться координатами, получившими название углов Эйлера:

 — угол собственного вращения;

 — угол прецессии;

 — угол нутации.