
4. Нестационарная фильтрация упругой жидкости и газа
Вывести уравнение пьезопроводности для упругой жидкости.
1)
линеаризованное уравнение состояния
упругой жидкости
![]()
2)
изменение пористости в зависимости от
давления
![]() .
.
3)
находим
![]() пренебрегая величинами второго порядка
малости (жс,)
−
пренебрегая величинами второго порядка
малости (жс,)
−
![]()
4)общее
уравнение фильтрации
![]()
5)
находим потенциал
![]() при μ=const,
k=const
при μ=const,
k=const
6)
получаем
![]() −
−
![]() ,
*
= m0ж
+с
–
коэффициент
упругоёмкости пласта
,
*
= m0ж
+с
–
коэффициент
упругоёмкости пласта
2. Дано выражение для распределения
давления
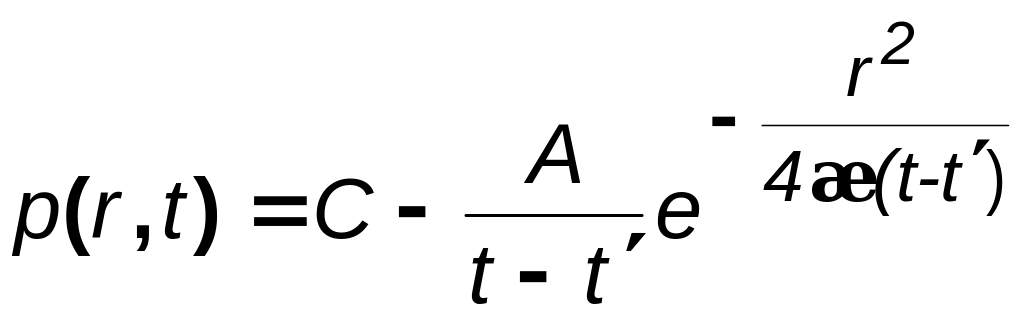 .
Вывести выражение для параметра С. (в
момент времени t
= t/
давление
в пласте было р
= рк
= const)
.
Вывести выражение для параметра С. (в
момент времени t
= t/
давление
в пласте было р
= рк
= const)
3. . Получить выражение КВД для периодически работающей скважины
7. УСТАНОВИВШАЯСЯ ПОТЕНЦИАЛЬНАЯ ПЛОСКАЯ (ДВУХМЕРНАЯ) ФИЛЬТРАЦИЯ
1. Фильтрационный поток от нагнетательной скважины к эксплуатационной (схема, постановка задачи, массовый дебит, модуль массовой скорости, время обводнения, площадь обводнения)
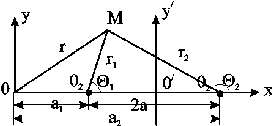
![]()
2)
![]()
3) Уравнение изобар
![]()
4) на контуре
эксплуатационной скважины –
![]() ;
на контуре нагнетательной скважины –
;
на контуре нагнетательной скважины –
![]() .–
.–
 .
.
5)
![]() ,
/
,
/![]()
![]() ,
,
![]()
6)
![]() Поместим начало координат в О1
− r1=x,
r2=2a-x
→
Поместим начало координат в О1
− r1=x,
r2=2a-x
→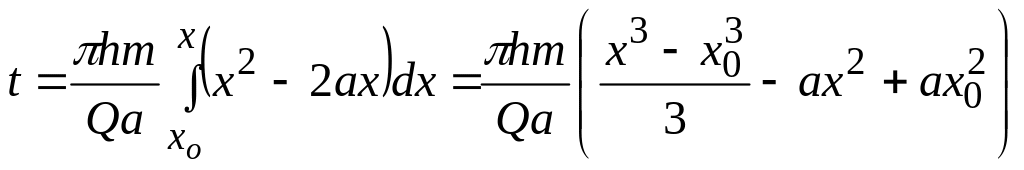 ;
;
![]() (
х=0; х0=2а);
(
х=0; х0=2а);
![]() (TQ=mh).
(TQ=mh).
2. Приток к группе скважин с удаленным контуром питания (постановка задачи, уравнения, порядок решения)
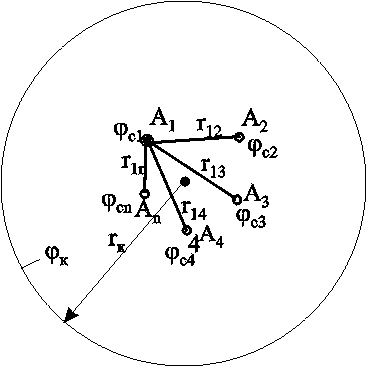
Исходная формула
2)
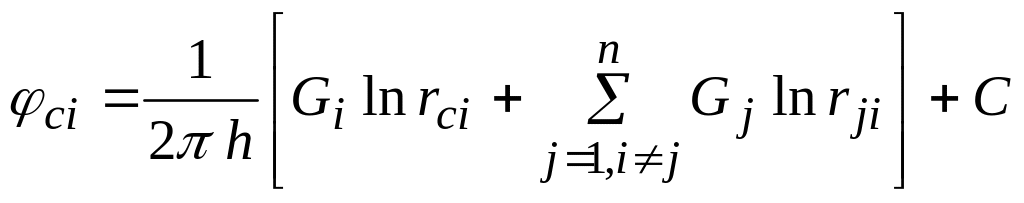 − n
уравнений +
− n
уравнений +
![]()
3. Приток к скважине в пласте с прямолинейным контуром питания (схема, постановка задачи, массовый дебит)
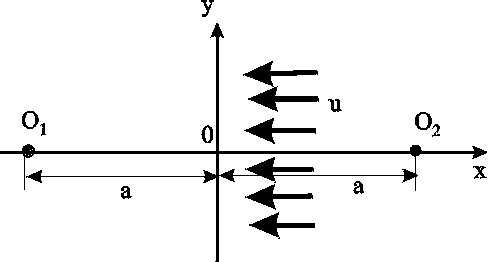
2) с гран. условиями
= к при r1 = r2 ,т.е. при r1/r2 = 1;
= с при r1 = rс , r2 2а, т.е. при r1/r2 rс /2а.
3)
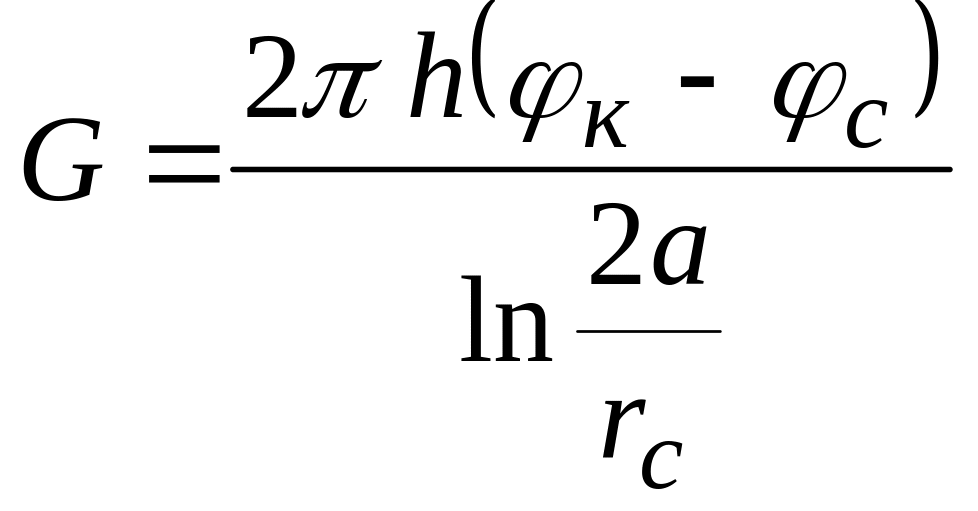
4. Приток к скважине, расположенной вблизи непроницаемой прямолинейной границы (схема, постановка задачи, массовый дебит)
1) метод отображения − сток − сток
2)
![]() с гран. условиями
с гран. условиями
= к при r1 = r2 ,т.е. при r1*r2 = rk2;
= с при r1 = rс , r2 2а, т.е. при r1*r2 rс *2а.
3)

5. Приток к скважинам кольцевой батареи (схема, постановка задачи, массовый дебит скважины, массовый дебит батареи)
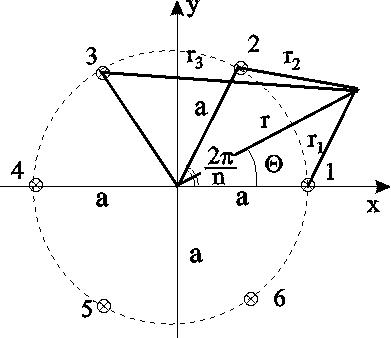
![]()
Граничные условия: на контуре питания =к=const, при rj=rк;
на контуре скважины =с=const, при r1=rс; rj(j1)=2a sin[(n-1)/n].
2)
![]() ,
,
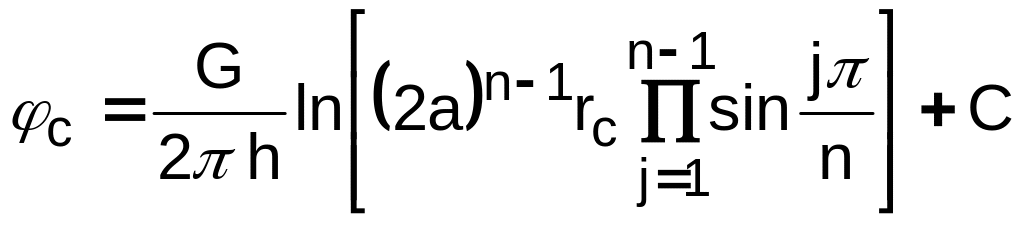
(![]() )
)![]() ;
;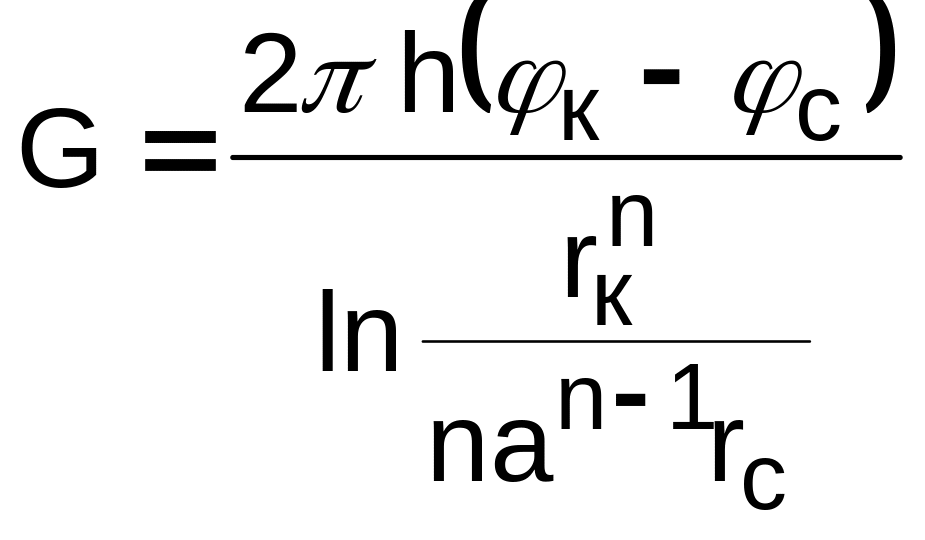 ;
;
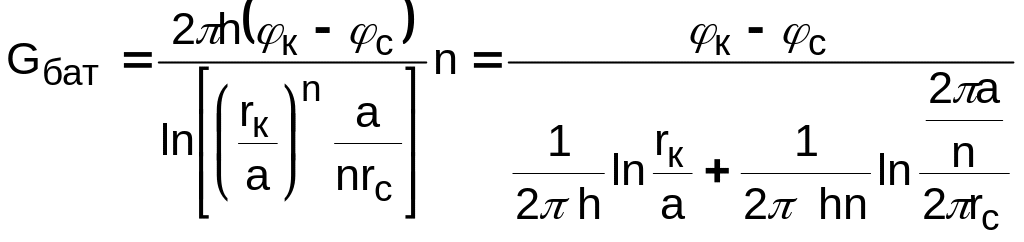
6. Приток к скважинам прямолинейной батареи (схема, постановка задачи, массовый дебит скважины, массовый дебит батареи)
1) Постановка: ; положим rк = L + a; a = n /(2 )
2)
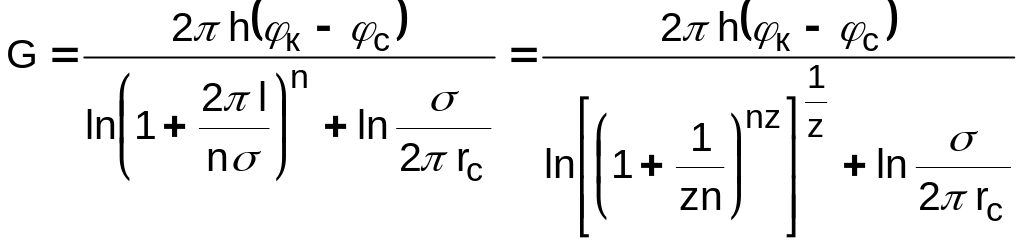 (z=
/ (2l))
(z=
/ (2l))
3) Переходим к
пределу при n;
![]() =e;
=e;
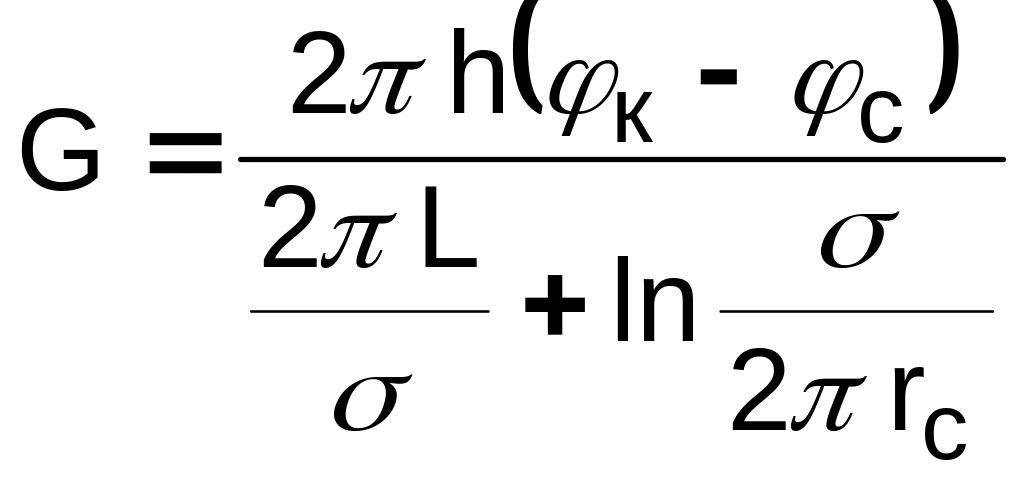 .
.
(L – расстояние от контура питания до батареи; –- расстояние между скважинами; h – толщина пласта).
![]()
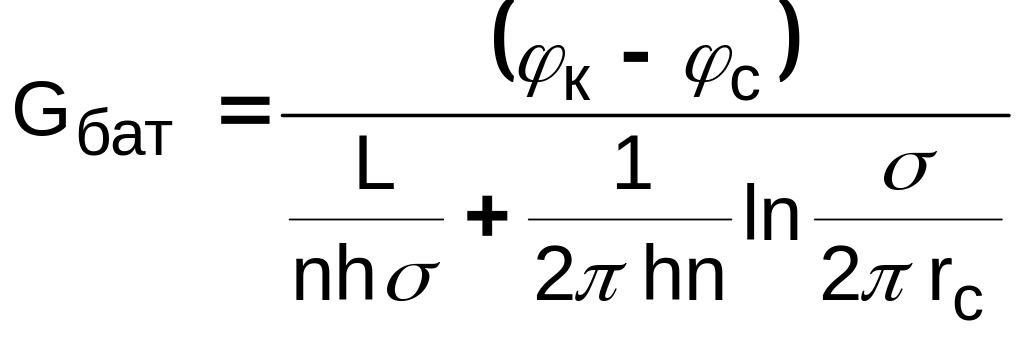 .
.
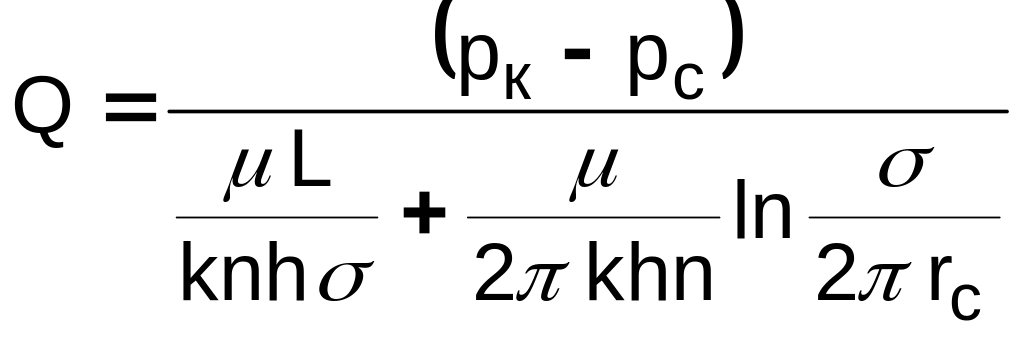 .
.
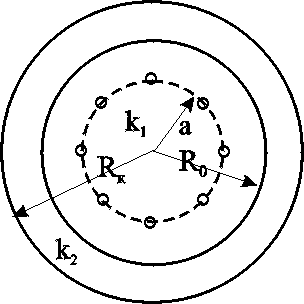
1) Rк >> a; 0 – потенциал на границе двух сред;
2) — область R0: приток к батареи (к=0);
3)
![]() ;
;
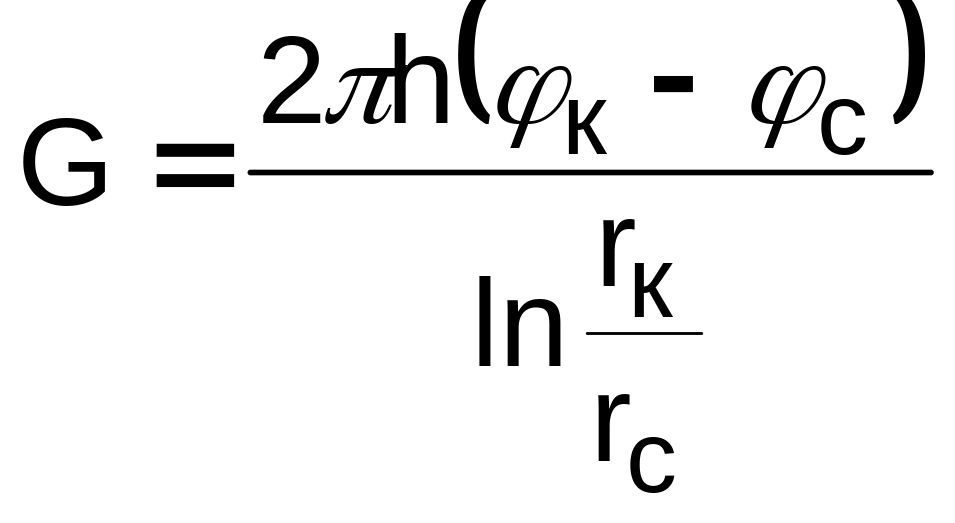 (ф.
Дюпюи) — область Rk
(приток к укрупненной скважине радиуса
R0)
(ф.
Дюпюи) — область Rk
(приток к укрупненной скважине радиуса
R0)
4)
= kФ+С, где
![]() (k=const)
в соотношение для
дебитов и исключаем Ф0
(k=const)
в соотношение для
дебитов и исключаем Ф0
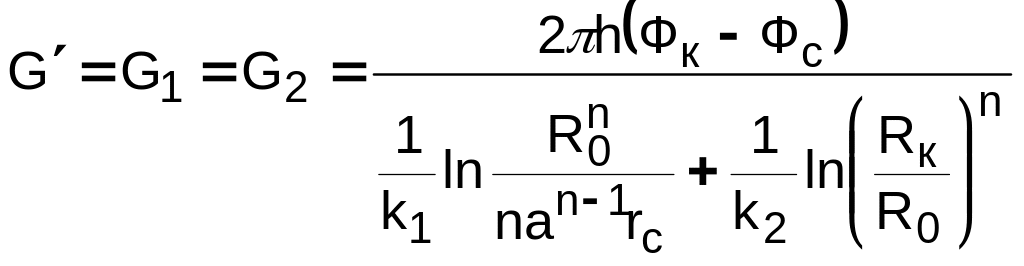 .
.
8. Дебит кольцевой батареи скважин при двухзональной неоднородности пласта (батарея расположена в области внешней неоднородности)

9. Доказать, что модуль производной от характеристической функции течения равен модулю массовой скорости фильтрации.
1)![]()
![]()
2)
Выносим во второй скобке множитель i
за
знак скобки. Используем соотношения
Коши-Римана
![]()
![]()
т.е.
![]() .
.
3) Т.к.
![]() имеем
имеем![]()
4)
![]()
1) А
=
А1
+
iA2
2)
![]()
3) потенциальная
функция
и
функция тока
![]()
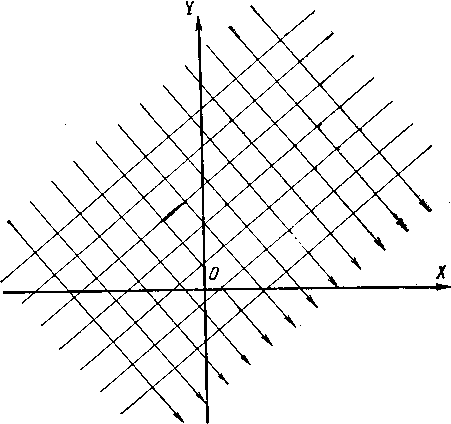
4) семейство эквипотенциальных линий: А1х – А2y = С — эквипотенциальные линии - прямые с угловым коэффициентом A1/А2.
5) семейство линий тока: А1у + А2х = С** — линии тока – прямые с угловым коэффициентом (-A2А1).
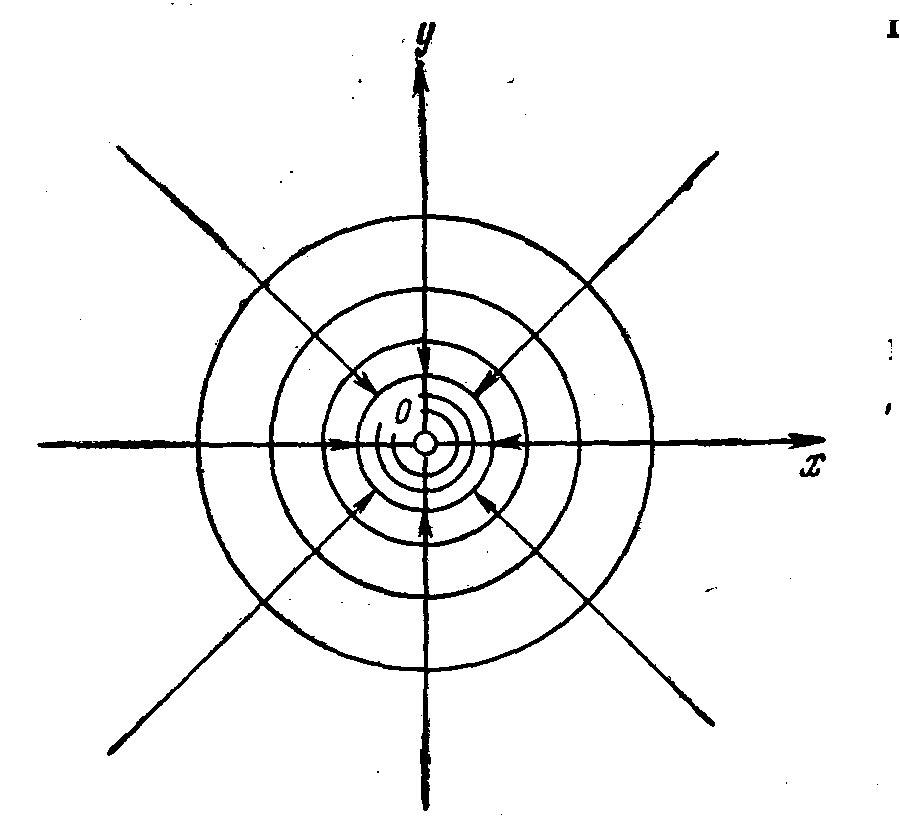
1) z = х +i y = r (cos θ + i sin θ) = reiθ
2) F(z) = A In (reiθ) = A In r + iAθ.
3) =Alnr; =Aθ. Уравнения эквипотенциальных линий – ν=const: концентрические окружности с центром в начале координат . Уравнения линии тока – θ = const: прямые, проходящие через начало координат.
4)
Массовая скорость равна производной
от характеристической функции
![]() .
Эта производная – комплексное переменное,
модуль которого равен массовой скорости
и представляет
собой множитель перед е-iθ.
Следовательно
.
Эта производная – комплексное переменное,
модуль которого равен массовой скорости
и представляет
собой множитель перед е-iθ.
Следовательно
![]() .
.
5)
Для
плоскорадиального потока
![]() ,
,
![]() ,
,
![]()
