30

ВИЩИЙ НАВЧАЛЬНИЙ ЗАКЛАД УКООПСПІЛКИ

ПОЛТАВСЬКИЙ УНІВЕРСИТЕТ ЕКОНОМІКИ І ТОРГІВЛІ

Кафедра економічної кібернетики

КУРСОВА РОБОТА

з дисципліни «Економіко-матиматичне моделювання» на тему:

«Аналітичні можливості нелінійної регресії»

Захищена на Виконала: студентка групи МЕ-21

„_____________” Спеціальності „ Міжнародна економіка ”

„____”___________2011р. Очкань Анастасія Юріївна

_____________

Підпис

Члени комісії___________ Керівник: к.е.н.,доцент

___________

___________ Негребецька Л.А.

__________________

Підпис

Полтава 2011

ЗМІСТ

Вступ……………………………………………………………………….…...3

РОЗДІЛ I. АНАЛІТИЧНІ МОЖЛИВОСТІ НЕЛІНІЙНОЇ РЕГРЕСІЇ

1. Аналітичні можливості нелінійної регресії в економічному моделюванні…………………………………………………………………...4

РОЗДІЛ II. ПРАКТИЧНЕ ЗАВДАННЯ

2.1. Побудова багатофакторної економіко-математичної моделі…...17

2.2. Аналіз моделі на наявність мультиколінеарності ……………….18

2.3. Оцінка достовірності моделі………………………………………24

2.4. Перевірка гіпотези про наявність гетероскедастичності ……….26

ВИСНОВКИ……………………………………………………………………..29

СПИСОК ЛІТЕРАТУРИ………………………………………………………...30

ВСТУП

Математичне моделювання є одним із найрозповсюдженіших способів дослідження різних процесів та явищ. Математичне моделювання включає в себе одержання та застосування математичних моделей. Аналітичний аспект його складається із змістовного опису об’єкта у математичній формі.

Математичне моделювання реалізується у 3-х взаємозв’язаних

стадіях:

− формалізація процесу, тобто побудова математичної

моделі шляхом складання математичного опису об’єкта та системи;

− програмування розв’язку задачі для знаходження

числових значень, параметрів (розробка алгоритмів та програм);

− встановлення адекватності математичної моделі, її

відповідності об’єкту моделювання.

Сучасна наука прагне пояснити процеси розвитку економічних систем виходячи із позитивного аналізу досвіду найефективніших із них та закономірностей етапів світового розвитку. Апроксимація даних з урахуванням їх статистичних параметрів відноситься до завдань регресії. Вони зазвичай виникають при обробці експериментальних даних, отриманих в результаті вимірювань процесів або фізичних явищ, статистичних за своєю природою. Завданням регресійного аналізу є підбір математичних формул, найкращим чином описують експериментальні дані.

РОЗДІЛ I. АНАЛІТИЧНІ МОЖЛИВОСТІ НЕЛІНІЙНОЇ РЕГРЕСІЇ

1.1Аналітичні можливості нелінійної регресії в економічному моделюванні

Надання зв’язку через лінійну функцію в тому випадку, коли існує нелінійне співвідношення, викличе помилки та спрощені або навіть неправильні висновки на основі аналітичного рівняння.

Питання про не лінійність форми рівняння необхідно вирішувати на стадії теоретичного аналізу. Аналіз повинен спиратися на суті взаємодіючих явищ та процесів і підкріплятися різними статистичними критеріями.

Існують різні форми нелінійних рівнянь регресії, але в загальному вигляді можна виділити два їх класи.[2]

1. Регресії нелінійні відносно включених в дослідження змінних, але лінійне за параметрами.

Це, наприклад, поліноми. В випадку парної регресії рівняння має наступний вигляд:

(1.1)

Множинна регресія (1.2)

маємо наступне рівняння:

(1.3)

Можливе застосування гіперболи, інших функцій. За допомогою стандартних програм для ЕВМ може бути створено будь-яке нелінійне поєднання змінних, що є лінійним відносно коефіцієнтів рівняння. Остання оцінюються за допомогою метода найменших квадратів.[6]

2. Регресії з нелінійними параметрами.

Найбільш роз поширеною є ступенева функція:

парна регресія:

(1.4)

множинна регресія:

(1.5)

Використання цих функцій обмежується складністю оцінювання параметрів рівняння. Це потребує спеціальних прийомів, програм для ЕВМ.

Якщо в рівняння множинної регресії змінні входять як , то регресія називається нелінійною.[4]

У загальному випадку нелінійна регресія записується в такому вигляді:

(1.6)

де параметри є сталими невідомими величинами, які підлягають статистичним оцінкам, а - випадкова величина, яка має нормальний закон розподілу з числовими характеристиками

(1.7)

(1.8)

і при цьому випадкові величини між собою не корельовані. Реалізуючи вибірку обсягом n, дістанемо систему нелінійних рівнянь виду:

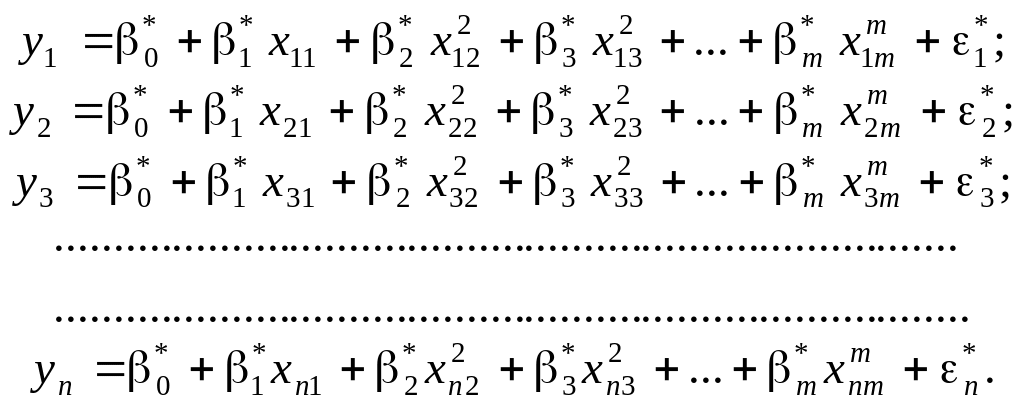(1.9)

Систему можна подати у векторно-матричній формі так:

(1.10)

Де

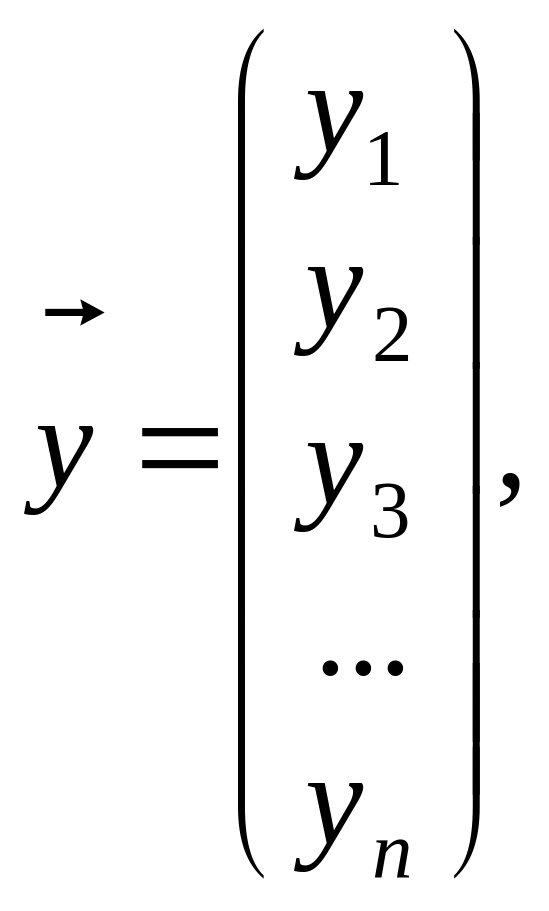
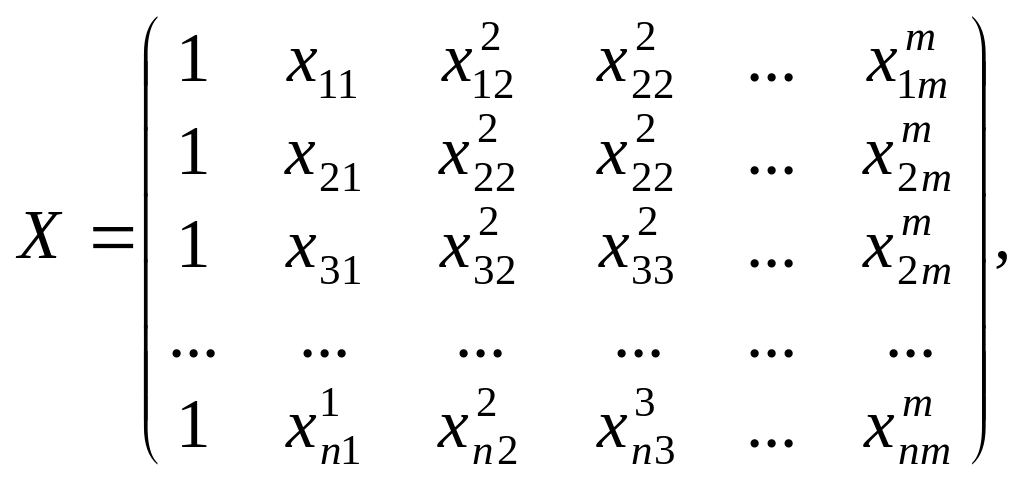
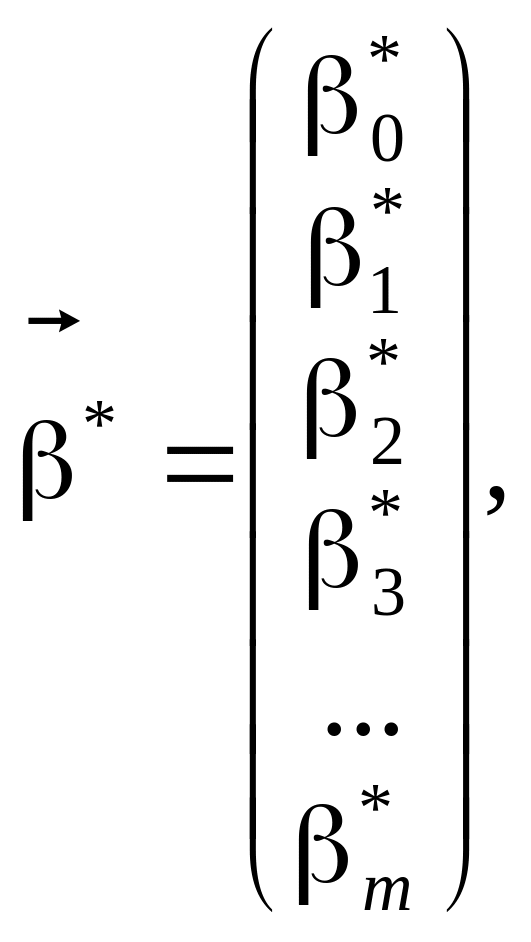
(1.11)

Тут є випадковими величинами, які визначаються шляхом обробки результатів вибірки і є точковими незміщеними статистичними оцінками відповідних параметрів рівняння, а саме:

Здійснивши аналогічні перетворення, які були зроблені для лінійної множинної регресії, дістанемо:

(1.12)

Тіснота зв’язку вимірюється з допомогою кореляційного відношення:

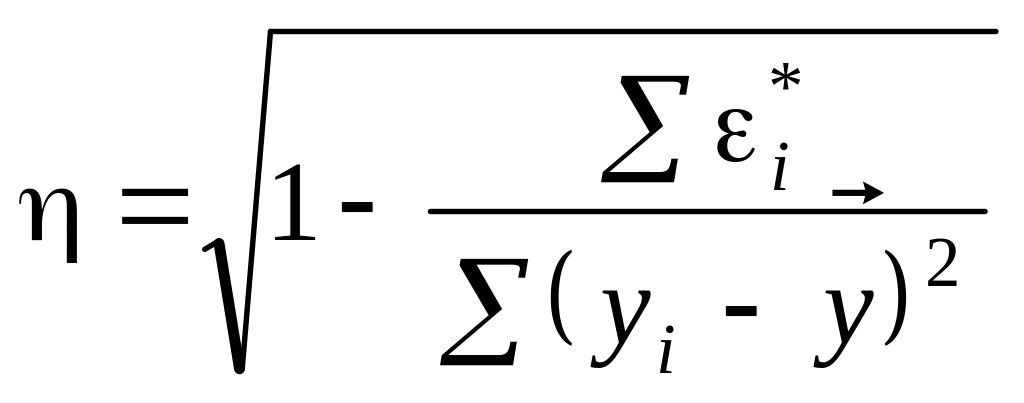
. (1.13)

Рівняння регресії в такому вигляді описує числове співвідно­шення варіації ознак х i у в середньому. Коефіцієнт пропорційності при цьому відіграє визначальну роль. Він показує, на скільки оди­ниць у середньому змінюється у зі зміною х на одиницю. У разі прямого зв'язку b - величина додатна, у разі оберненого - від'ємна.[4,7]

Подаючи у як функцію х, тим самим абстрагуються від мно­жинності причин, штучно спрощуючи механізм формування ва­ріації у. Аналіз причинних комплексів здійснюється за допомо­гою множинної регресії.

Різні явища по-різному реагують на зміну факторів. Для то­го щоб відобразити характерні особливості зв'язку конкретних явищ, статистика використовує різні за функціональним видом регресійні рівняння. Якщо зі зміною фактора х результат y змі­нюється більш-менш рівномірно, такий зв'язок описується лі­нійною функцією Y=a+bx. (1.14) Коли йдеться про нерівномірне співвідношення варіацій взаємозв'язаних ознак (наприклад, ко­ли прирости значень у зі зміною х прискорені чи сповільнені або напрям зв'язку змінюється), застосовують нелінійні регре­сії, зокрема:

степеневу

Y=ax^b (1.15)

гіперболічну

Y=a+b/x (1.16)

параболічну

Y = а + bx + сх² (1.16) тощо.

Вибір та обґрунтування функціонального виду регресії ґрун­тується на теоретичному аналізі суті зв'язку. Нехай вивчається зв'язок між урожайністю та кількістю опадів. Надто мала і надто велика кількість опадів спричинюють зниження врожайності, ма­ксимальний її рівень можливий за умови оптимальної кількості опадів, тобто зі збільшенням факторної ознаки (опади) урожай­ність спершу зростає, а потім зменшується. Залежність такого роду описується параболою Y = а + bx + сх² (1.17)

Вивчаючи зв'язок між собівартістю у та обсягом продукції х, використовують рівняння гіперболи Y = а + b/x, де a - пропорційні витрати на одиницю продукції, b - постійні витрати на весь ви­пуск.[8,12]

Зауважимо, що теоретичний аналіз суті зв'язку, хоча й дуже важливий, лише окреслює особливості форми регресії і не може точно визначити її функціонального виду. До того ж у конкрет­них умовах простору і часу межі варіації взаємозв'язаних ознак х і у значно вужчі за теоретично можливі. І якщо кривина регресії невелика, то в межах фактичної варіації ознак зв'язок між ними досить точно описується лінійною функцією. Цим значною мі­рою пояснюється широке застосування лінійних рівнянь регресії:

Y = а + bx (1.18)

Параметр b (коефіцієнт регресії) - величина іменована, має розмірність результативної ознаки і розглядається як ефект впливу х на у. Параметр а - вільний член рівняння регресії, це значення у при х = 0. Якщо межі варіації x не містять нуля, то цей параметр має лише розрахункове значення.

Параметри рівняння регресії визначаються методом наймен­ших квадратів, основна умова якого - мінімізація суми квадра­тів відхилень емпіричних значень у від теоретичних Y:

(у-Y)² =min (1.19)

Математично доведено, що значення параметрів а та b, при яких мінімізується сума квадратів відхилень, визначаються із си­стеми нормальних рівнянь:

y=na+bx,

xy=ax+bx² (1.20)

Розв'язавши цю систему, знаходимо такі значення параметрів:

b=(nxy-xy)/(nx²-xx)

a =y-bx (1.21)

Р івняння регресії відбиває закон зв'язку між х і у не для окре­мих елементів сукупності, а для сукупності в цілому; закон, який абстрагує вплив інших факторів, виходить з принципу «за інших однакових умов». Вплив інших окрім х факторів зумовлює відхилення емпіричних значень у від теоретичних у той чи інший бік. Відхилення (у - Y) називають залишками і позначають символом е. Залишки, як правило, ме­нші за відхилення від середньої, тобто (у - Y) < (у - у). [12]

Відповідно загальна дисперсія

(1.22)

залишкова дисперсія

(1.23)

У невеликих за обсягом сукупностях коефіцієнт регресії схи­льний до випадкових коливань. Тому слід перевірити його істот­ність. Коли зв'язок лінійний, істотність коефіцієнта регресії пе­ревіряють за допомогою t-критерію (Стьюдента), статистична характеристика якого для гіпотези Н₀:b=0 визначається від­ношенням коефіцієнта регресії b до власної стандартної похибки

(1.24)

Стандартна похибка коефіцієнта регресії залежить від варіації факторної ознаки б_х², залишкової дисперсії б_е² і числа ступенів свободи k = п - т, де т - кількість параметрів рівняння регресії:

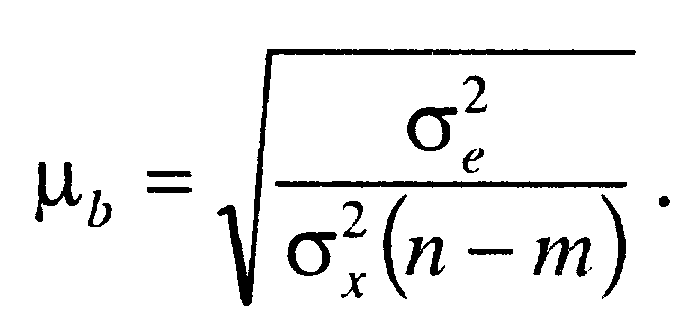(1.25)

Для лінійної функції т = 2.

Для коефіцієнта регресії, як і для будь-якої іншої випадкової величини, визначаються довірчі межі

(1.26)

Важливою характеристикою регресійної моделі є відносний ефект впливу фактора х на результат у - коефіцієнт еластичності:

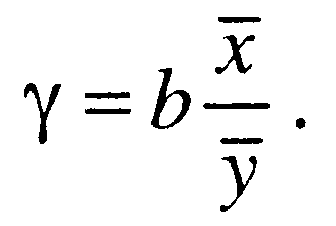(1.27)

Він показує, на скільки процентів у середньому змінюється ре­зультат у зі зміною фактора х на 1%.[3]

Оцінити відносний ефект впливу фактора х на результат у мож­на безпосередньо на основі степеневої функції Y = ах^b, параметр b якої є коефіцієнтом еластичності. Степенева функція зводиться до лінійного виду логарифмуванням lgY = Iga + blgx. До класу сте­пеневих належать функції споживання, виробничі функції тощо.

В имірювання щільності нелінійного зв'язку ґрунтується на співвідношенні варіацій теоретичних та емпіричних (фактич­них) значень результативної ознаки у. Відхилення індивідуального значення ознаки у від сере­дньої (у-у) можна розкласти на дві складові. У регресійному аналізі це відхилення від лінії регресії (у - Y) та відхилення лінії регресії від середньої (Y - у).[5]

Очевидно, значення факторної дисперсії буде тим біль­шим. чим сильніший вплив фактора х на у. Відношення фактор­ної дисперсії до загальної розглядається як міра щільності коре­ляційного зв'язку і називається коефіцієнтом детермінації:

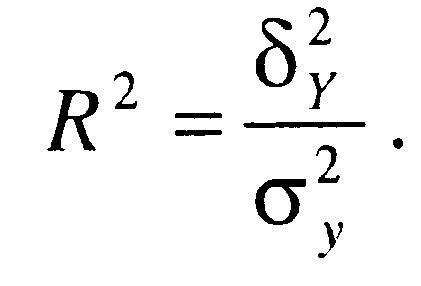(1.28)

Корінь квадратний з коефіцієнта детермінації називають інде­ксом кореляції R. Коли зв'язок лінійний, R=|r|, що підтвер­джують обчислення:

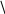
R = R². (1.29)

Тому за відомим лі­нійним коефіцієнтом кореляції г можна визначати внесок ознаки х у варіацію ознаки у. Так, при r = 0,6 можна сказати, що 36% ва­ріації у залежить від варіації х.

На таких самих засадах ґрунтується оцінювання щільності зв'язку за даними аналітичного групування.

Обчислення та інтерпретація коефіцієнта детермінації R² і ко­реляційного відношення ² показують: ці характеристики щіль­ності зв'язку за змістом ідентичні, вони характеризують внесок фактора х у загальну варіацію результату у.[9]

Показниками тісноти зв'язку є: для парної лінійної моделі - коефіцієнт парної лінійної кореляції; для множинної лінійної моделі - коефіцієнт множинної кореляції; для нелінійних моделей (парних і багатофакторних ) -кореляційне відношення.

Коефіцієнт парної кореляції для лінійної моделі розраховується:

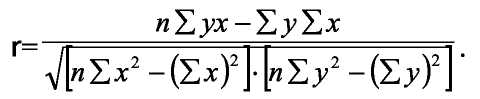(1.30)

Коефіцієнт множинної кореляції (R) і кореляційне відношення - для множинних і парних нелінійних моделей (tj) розраховуються за формулою:

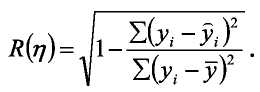(1.31)

Показники тісноти зв'язку можуть змінюватися в таких інтервалах:

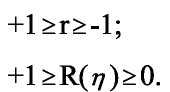(1.32)

Коефіцієнт множинної кореляції або множинне кореляційне відношення у квадраті (R², tj²) називається коефіцієнтом детермінації. Останній відображає частку впливу відібраних факторів на величину результативного показника.

Показники: середня помилка апроксимації; середнє квадратичне відхилення між фактичними і розрахунковими значеннями функції - абсолютне і відносне; середнє відхилення між фактичними і розрахунковими значеннями функції - абсолютне і відносне, які використовуються для оцінки рівняння часового тренда, у рівній мірі застосовуються і для оцінки статистичної адекватності економіко-статистичних моделей. Для останніх додатково визначається залишкова дисперсія:

(1.33)

де m - число факторів, які включені у модель.

Залишкова дисперсія може бути використана і для оцінки рівняння часового тренда.[13]

Результати спостережень над ознаками Х і Y наведено у таблиці:

i	хі	уі
1	1	8
2	2	4
3	4	2
4	6	1
5	8	0
6	10	6
7	12	8
8	14	10

Таб 1.1

Потрібно:

1) визначити точкові незміщені статистичні оцінки для параметрів нелінійної регресії

(1.34)

2) обчислити η.

Розв’язання. З результатів вибірки маємо:

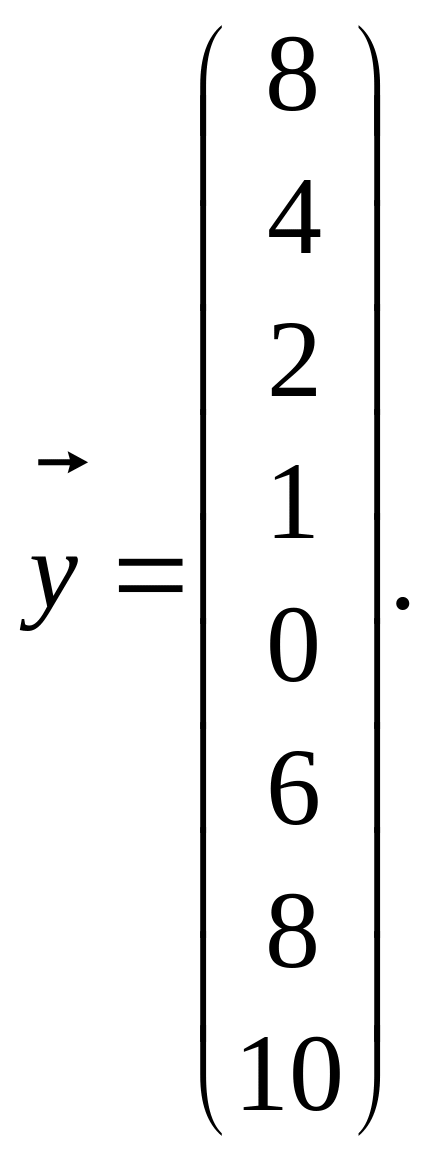(1.35)

Використовуючи (566), дістанемо:

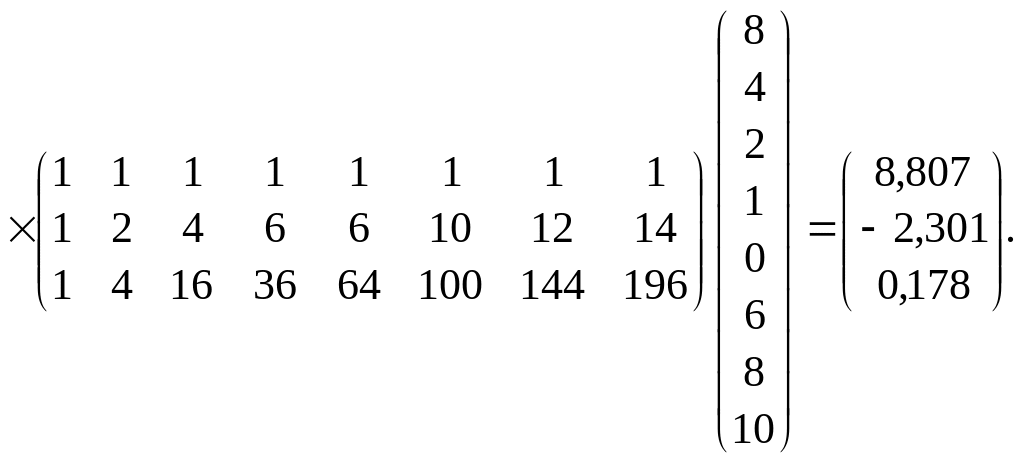
(1.36)

Таким чином, маємо:

(1.37)

Для визначення η застосовуємо табличний запис:

i	хі	уі
1	1	8	6,684	1,732
2	2	4	4,917	0,841
3	4	2	2,451	0,203
4	6	1	1,409	0,167
5	8	0	1,791	3,208
6	10	6	3,597	5,774
7	12	8	6,827	1,376
8	14	10	11,481	2,193
		39		15,494

Таб 1.2

Отже, дістали (1.38)

Оскільки

(1.39)

то

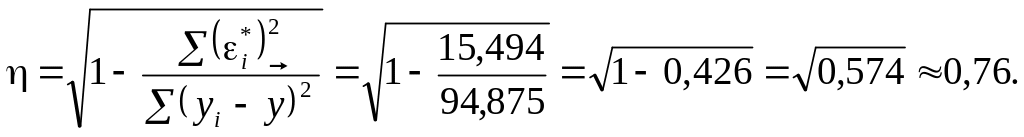(1.40)

За результатами спостережень ознак генеральної сукупності Х і Y:

i	хі	уі
1	1	30
2	2	20
3	4	10
4	5	8
5	8	6
6	10	1

Таб 1.3

Знайти точкові незміщені статистичні оцінки для параметрів рівняння нелінійної регресії

(1.41)

Обчислити η.

Розв’язання. За результатами вибірки маємо:

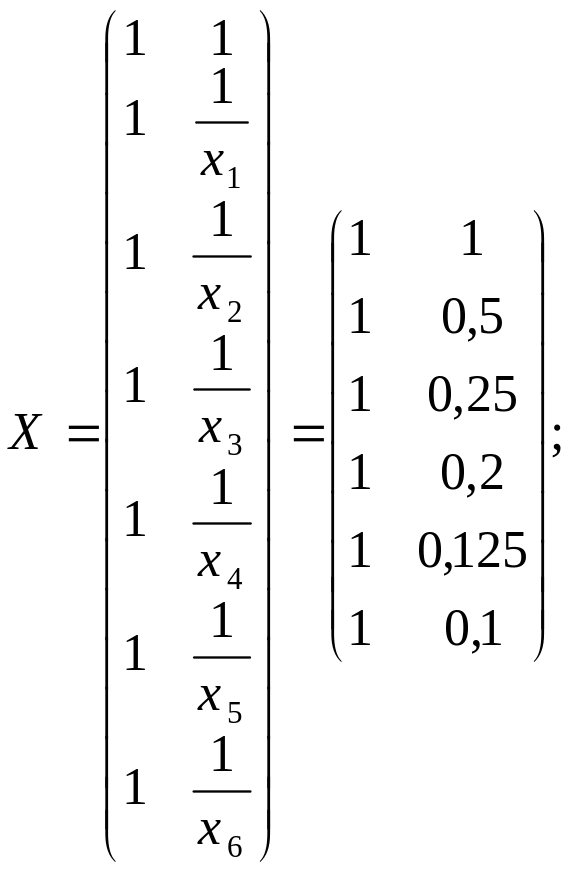
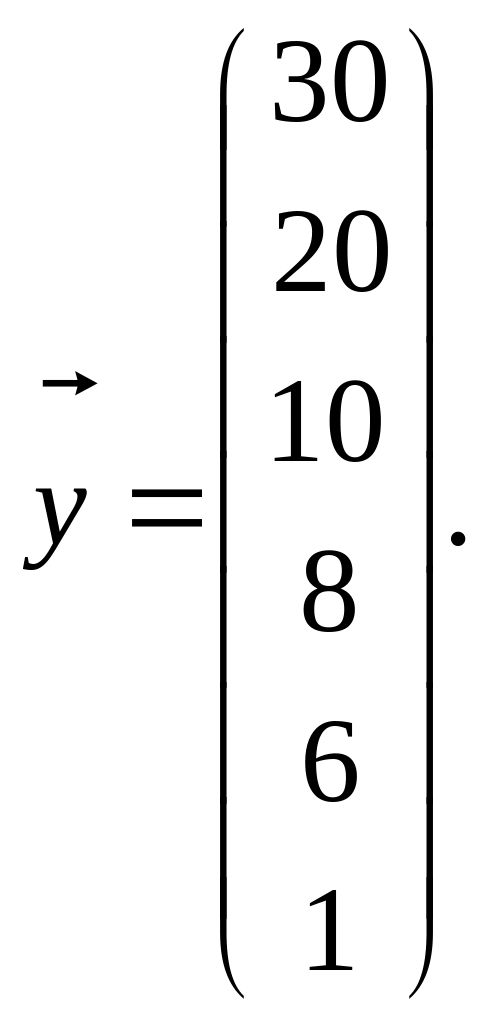(1.42)

Знаходимо:

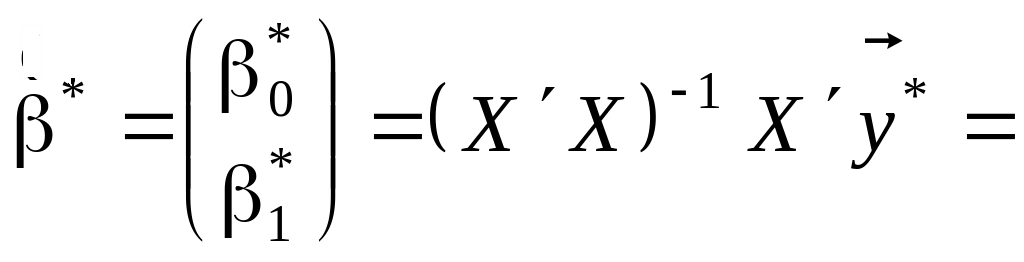
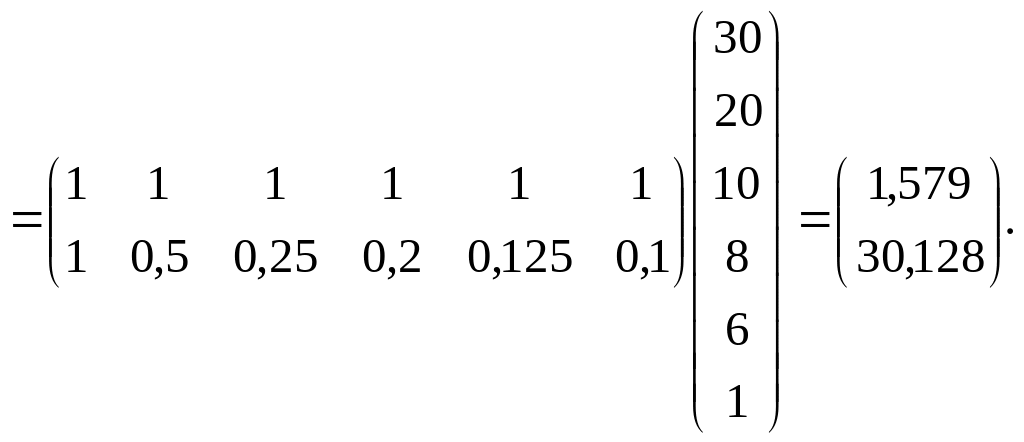
(1.43)

Отже, маємо:

(1.44)

Для обчислення η застосовуємо таблицю:

i	хі	уі
1	1	30	31,707	2,914
2	2	20	16,643	11,269
3	4	10	9,111	0,790
4	5	8	7,6046	0,156
5	8	6	5,345	0,429
6	10	1	4,5918	12,901
		75		28,459

Таб 1.4

Таким чином, дістали:

(1.45)

Оскільки то

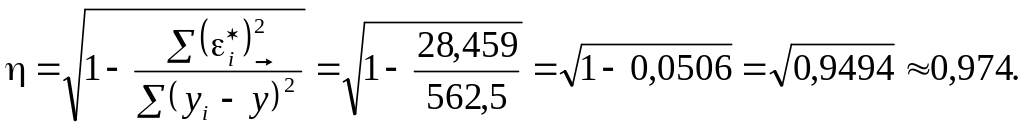(1.46)

Отже,

Нелінійна модель за параметрами.

В економічному аналізі розглядають нелінійну регресію за параметрами, що подається в такому найпростішому вигляді:

. (1.47)

Такі функції регресії використовують для вимірювання впливу на обсяг виробництва таких чинників, як кількість зайнятих у виробництві робітників, обсяг основних фондів тощо.[1,7,10]

У рівнянні є невідомими величинами, але сталими, які оцінюються точковими незміщеними статистичними оцінками котрі визначаються обробкою результатів вибірки.

Для врахування впливу випадкових збудників, які відхиляють теоретично прогнозовану регресію, вводиться випадкова величина Тоді нелінійна модель відносно параметрів набуває такого вигляду:

. (1.48)

Статистичною оцінкою рівняння буде:

. (1.49)

Для визначення точкових незміщених статистичних оцінок використовуємо, як і в попередніх моделях, метод найменших квадратів, а для цього рівняння подано в такому вигляді:

. (1.50)

Здійснивши вибірку обсягу n, дістанемо систему рівнянь, яку у векторно-матричній формі можна записати так:

де

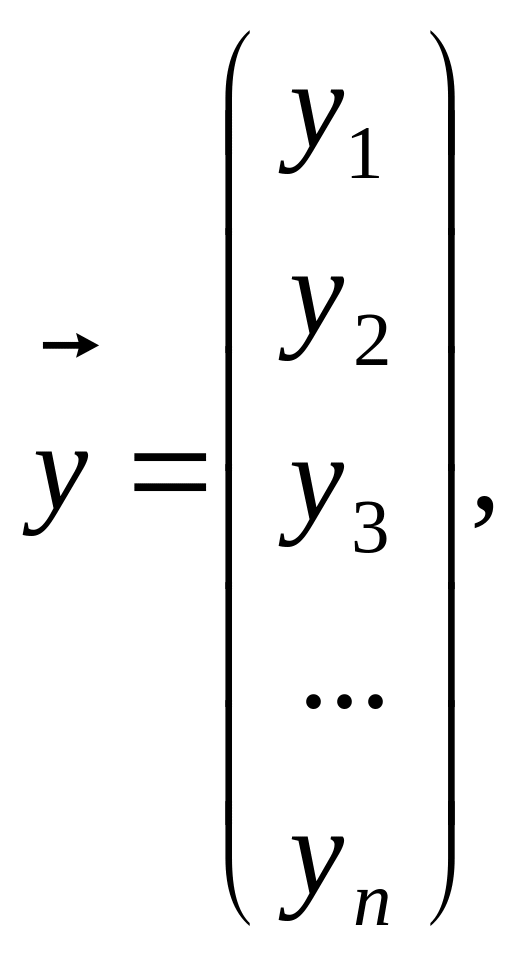
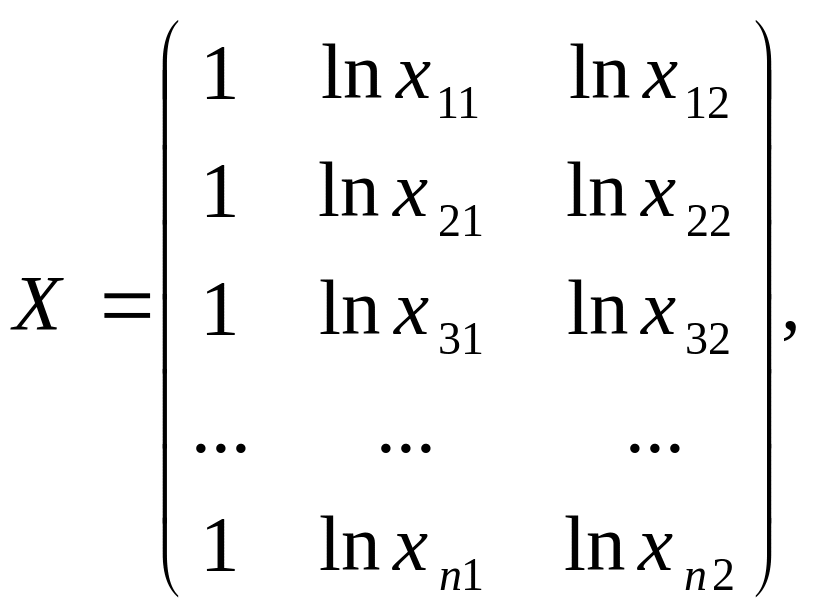
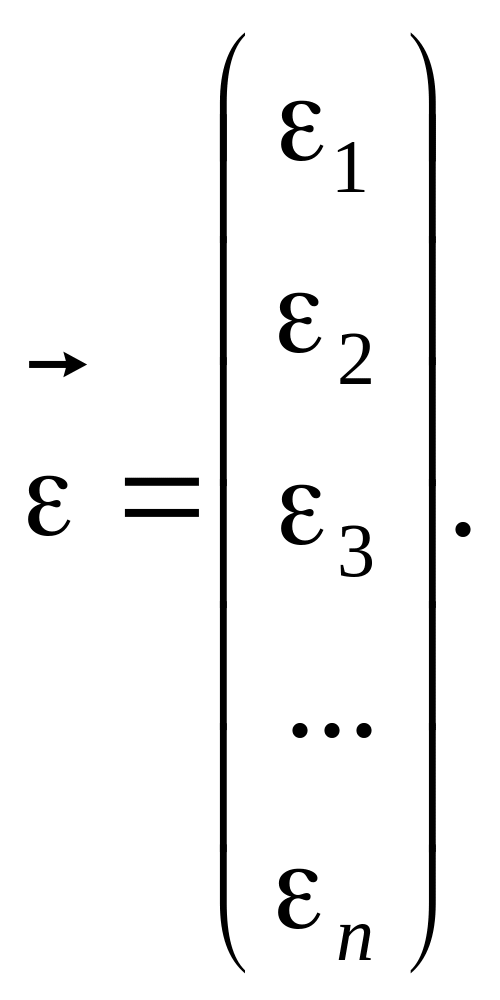(1.51)

Тоді, за аналогією з попередніми випадками, компоненти вектора визначають із рівняння.[14]

РОЗДІЛ II. ПРАКТИЧНА ЧАСТИНА

2.1.Побудувати лінійну багатофакторну економіко-математичну модель

залежності фактору Y від факторів X_i

Ідентифікуємо дані:

Y – (залежний фактор);

Х –(незалежний фактор).

, (2.1)

де а₀, а₁ – коефіцієнти лінійної моделі, е – випадкова складова

Для того, щоб обчислити параметри лінійної регресії, в MS Excel передбачена вбудована функція ЛИНЕЙН (Таблиця 1.1), яка обчислює основні параметри регресії (коефіцієнти регресії, стандартні похибки коефіцієнтів, коефіцієнт детермінації, стандартну похибку, критерій Фішера, сума квадратів різниць між фактичним та середнім значенням фактора Y та суму квадратів залишків). Всі інші параметри можуть бути обчислені згідно означень.

Застосувавши функцію ЛИНЕЙН, одержимо:

Таблиця 1.1. Основні параметри регресії

0,39832	0,737647	0,7973	5,979895
0,242594	0,175711	0,227756	0,467686
0,992294	0,435834	#Н/Д	#Н/Д
472,1768	11,000	#Н/Д	#Н/Д
269,0717	2,089464	#Н/Д	#Н/Д

В результаті обчислень отримано:

a0=	5,979895		Sa0=	0,467686		R2=	0,992294
a1=	0,7973		Sa1=	0,227756		E=	0,435834
a2=	0,737647		Sa2=	0,175711		F=	472,1768
a3=	0,39832		Sa3=	0,242594		n-k=	11,000
						k-1=	3

a₀; a₁; a₂; a₃ –коефіцієнти регресії;

Sa₀; Sa₁; Sa₂; Sa₃ – стандартні похибки коефіцієнтів;

R²- коефіцієнт детермінації;

Е – стандартна похибка;

F – критерій Фішера;

n-k – число ступенів вільності

Стандартна похибка моделі Е=0,666. Значення не перевищує критичне. Отже модель якісна.

(2.1)

Критерій Фішера застосовується для перевірки рівності дисперсій двох вибірок. Його відносять до критеріїв розсіювання. При перевірці гіпотези положення (гіпотези про рівність середніх значень у двох вибірках) з використанням критерію Стьюдента, має сенс перевірити гіпотезу про рівність дисперсій. Якщо вона правильна, то для порівняння середніх можна скористатися більш потужним критерієм. У регресійному аналізі критерій Фішера дозволяє оцінювати значимість лінійних регресійних моделей. Зокрема, він використовується в крокової регресії для перевірки доцільності включення або виключення незалежних змінних (ознак) у регресійну модель. У дисперсійному аналізі критерій Фішера дозволяє оцінювати значимість факторів і їх взаємодії. Критерій Фішера заснований на додаткових припущеннях про незалежність і нормальності вибірок даних. Перед його застосуванням рекомендується виконати перевірку нормальності.

Отже, так модель відповідає хоча б одній з вище поданих характеристик, можемо вважати її якісною, тобто адекватною економічному процесу.