
- •Введение
- •1.Стандартное преобразование Фурье
- •1.1. Пример анализа с использованием преобразования Фурье.
- •1.3. Анализ применимости преобразования Фурье.
- •2. Кратковременное преобразование Фурье
- •2.1. Общие сведения.
- •2.2. Анализ применимости кратковременного преобразования Фурье.
- •2.3. Принцип Гейзенберга.
- •3. Непрерывное wavelet-преобразование и анализ со многими разрешениями.
- •3.1.Общие сведения
- •3.2.Определение непрерывного wavelet - преобразования
- •3.3. Примеры материнских wavelet-ов
- •3.4. Локализующие свойства и интерпретация
- •3.5. Свойства cwt
- •3.6. Примеры непрерывного wavelet-преобразования
- •3.7. Дискретизация непрерывного wavelet-преобразования.
- •3.8. Практическое использование непрерывного wavelet-преобразования
- •4. Дискретное wavelet-преобразование
- •4.1. Кратномасштабный анализ
- •4.2. Wavelet-ряды дискретного времени
- •4.3. Матричное описание дискретного wavelet-преобразования
- •4.4. Описание dwt посредством банков фильтров.
- •5. Применение дискретного wavelet-преобразования.
- •5.1. Применение wavelet-преобразования для сжатия сигнала.
- •5.2. Удаление шума из сигнала.
- •6. Адаптивные ортогональные преобразования.
- •6.1. Пакеты вейвлетов.
- •7. Работа с приложением gui wavemenu пакета программ matlab
- •7.1 Описание Wavemenu
- •7.1.1. Вызов Wavemenu
- •7.1.2. Структура Wavemenu
- •7.1.3. Меню для разделов Wavemenu
- •7.1.4. Экспорт и импорт информации из Wavemenu
- •7.2 Использование Wavemenu для обработки сигналов
- •7.2.1. Получение информации по конкретным wavelet-ам
- •7.2.2. Использование дискретного wavelet-преобразования
- •Очистка сигнала от шумов на основе dwt
- •Сжатие сигнала на основе dwt в Wavemenu
- •7.2.3. Использование разложения по wavelet-пакету
- •Очистка сигнала от шумов с использованием wavelet-пакет
- •Сжатие сигнала с использованием wavelet-пакет
- •7.2.4 Работа с непрерывным wavelet-преобразованием
- •Литература
- •197376, С.-Петербург, ул. Проф. Попова, 5
4. Дискретное wavelet-преобразование
4.1. Кратномасштабный анализ
Теория кратномасштабного анализа [3],[4] базируется на теории функциональных пространств.
Под кратномасштабным анализом пространства
![]() понимается описание исходного пространства
через иерархические вложенные
подпространстваVm, которые
не пересекаются, и объединение которых
дает нам в пределе
понимается описание исходного пространства
через иерархические вложенные
подпространстваVm, которые
не пересекаются, и объединение которых
дает нам в пределе![]() ,
то есть
,
то есть
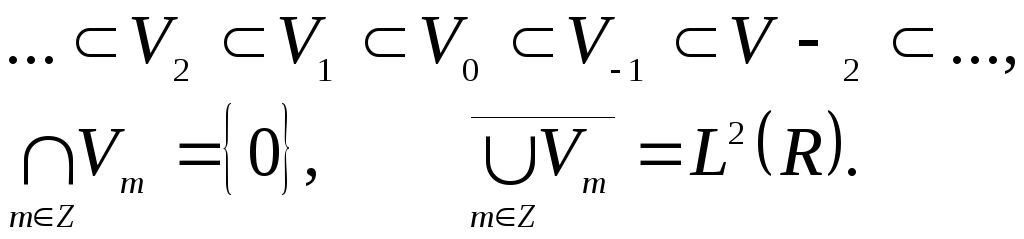
Далее, эти пространства имеют следующее
свойство: для любой функции
![]() ,
ее сжатая версия будет принадлежать
пространству
,
ее сжатая версия будет принадлежать
пространству![]() ,
,
![]() .
.
И, наконец, последнее свойство
кратномасштабного анализа: существует
такая функция
![]() ,
что ее сдвиги
,
что ее сдвиги![]() образуют ортонормированный базис
пространства
образуют ортонормированный базис
пространства![]() .
.
На рис. 10. схематично показаны данные вложенные пространства.
Так как функции
![]() образуют ортонормированный базис
пространства
образуют ортонормированный базис
пространства![]() ,
то функции
,
то функции
![]()
образуют ортонормированный базис
пространства
![]() .
Эти базисные функции называются
масштабирующими [3]. Из кратномасштабного
анализа, определенного выше, следует,
что функция
.
Эти базисные функции называются
масштабирующими [3]. Из кратномасштабного
анализа, определенного выше, следует,
что функция![]() в
в![]() может быть представлена множеством
последовательных ее приближений
может быть представлена множеством
последовательных ее приближений![]() в
в![]() .
Другими словами, функция
.
Другими словами, функция![]() есть предел аппроксимаций
есть предел аппроксимаций![]() приm, стремящемся к минус бесконечности:
приm, стремящемся к минус бесконечности:
![]()
Отсюда появляется возможность анализа
функции или сигнала на различных уровнях
разрешения, или масштаба. Переменная mназывается масштабным коэффициентом,
или уровнем анализа. Еслиmвелико,
то функция в![]() есть грубая аппроксимация
есть грубая аппроксимация![]() и детали отсутствуют. При малых
значенияхmимеет место точная
аппроксимация.
и детали отсутствуют. При малых
значенияхmимеет место точная
аппроксимация.
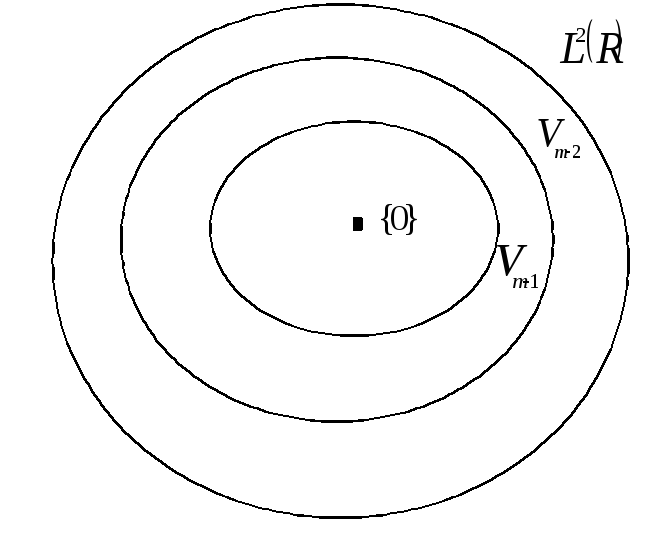
Рис. 10. Кратномасштабное представление
![]() .
.
Из определения кратномасштабного
анализа следует, что все функции в
![]() могут быть представлены как линейная
комбинация масштабирующих функций. В
действительности,
могут быть представлены как линейная
комбинация масштабирующих функций. В
действительности,![]() есть ортогональная проекция
есть ортогональная проекция![]() на
на![]() ,
,
![]() .
.
Так как
![]() ,
можно записать
,
можно записать
![]() ,
(26)
,
(26)
где
![]() - некоторая последовательность. Равенство
(26) является одним из основных в теории
wavelet -анализа и имеет различные названия
в литературе. Чаще всего встречается
название - масштабирующее уравнение
(refinement equation).
- некоторая последовательность. Равенство
(26) является одним из основных в теории
wavelet -анализа и имеет различные названия
в литературе. Чаще всего встречается
название - масштабирующее уравнение
(refinement equation).
Функция
![]() и последовательность
и последовательность![]() тесно связаны между собой. Выведем
соответствующие отношения. Из (26) можно
получить
тесно связаны между собой. Выведем
соответствующие отношения. Из (26) можно
получить
![]() .
(27)
.
(27)
Выполним операцию скалярного произведения
![]() с обеих сторон равенства (27):
с обеих сторон равенства (27):
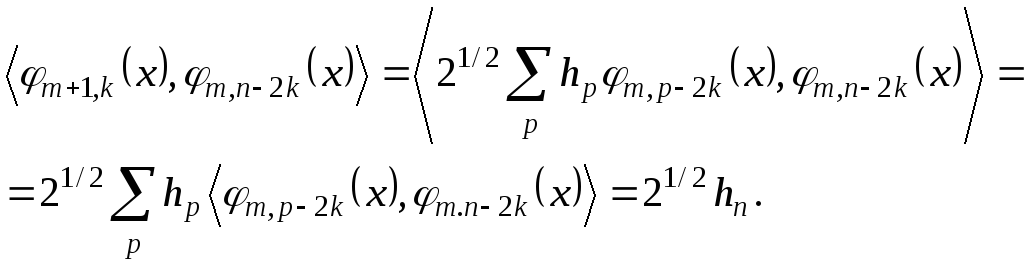 (28)
(28)
Отметим, что это равенство выполняется
для любого
![]() .
Далее, если переписать (28) в частотной
области, можно получить
.
Далее, если переписать (28) в частотной
области, можно получить
![]() .
(29)
.
(29)
Рекурсивно повторяя формулу (29), получается выражение
![]() .
(30)
.
(30)
Итак, последовательность
![]() тесно связана с масштабирующей функцией.
Кроме того, концепция кратномасштабного
анализа накладывает на нее дополнительные
ограничения.
тесно связана с масштабирующей функцией.
Кроме того, концепция кратномасштабного
анализа накладывает на нее дополнительные
ограничения.
Во-первых, интегрируя (26) по всей числовой
оси
![]() ,
можно получить
,
можно получить
![]() .
(31)
.
(31)
Во-вторых, в силу ортонормальности базисных функций,
![]() .
.
Третье свойство последовательности
![]() сформулируем в спектральной области.
Из записи условия ортонормальности
функций
сформулируем в спектральной области.
Из записи условия ортонормальности
функций![]() в области спектра
в области спектра
![]()
можно получить следующее выражение:
![]() .
(32)
.
(32)
Равенство (27) эквивалентно тому, что![]() .
Тогда из (32) следует, что
.
Тогда из (32) следует, что![]() .
.
4.2. Wavelet-ряды дискретного времени
В большинстве приложений мы имеем дело
с дискретными сигналами. Поэтому, с
точки зрения практики представляют
интерес дискретные аналоги CWT . К
сожалению, формулы для wavelet-преобразования
дискретного времени нельзя получить
простой дискретизацией соответствующих
формул для непрерывного времени. Также
невозможно определить кратномасштабный
анализ для дискретных сигналов, так как
не существует базисных функций,
масштабированные и смещенные версии
которых давали бы нам базис пространства
![]() ,
пространства квадратично суммируемых
последовательностей бесконечной длины.
,
пространства квадратично суммируемых
последовательностей бесконечной длины.
Рассмотрим сначала, как можно получить представление CWT в виде wavelet-рядов для дискретного времени (DTWS -discrete time wavelet set).
Пусть имеется некоторая непрерывная
функция
![]() .
Наш дискретный сигнал
.
Наш дискретный сигнал![]() представим как последовательность
коэффициентов при масштабирующих
функциях, по которым раскладывается
представим как последовательность
коэффициентов при масштабирующих
функциях, по которым раскладывается![]() :
:
![]() .
.
где
![]() .
Другими словами, мы интерпретируем наш
сигнал как последовательность
коэффициентов разложения, полученную
в ходе кратномасштабного анализа функции
.
Другими словами, мы интерпретируем наш
сигнал как последовательность
коэффициентов разложения, полученную
в ходе кратномасштабного анализа функции![]() .
Тогда мы можем вычислить аппроксимации
этой функции, принадлежащие пространствам
.
Тогда мы можем вычислить аппроксимации
этой функции, принадлежащие пространствам![]() .
Пространства
.
Пространства![]() не имеют значения при данной интерпретации.
не имеют значения при данной интерпретации.
Согласно концепции кратномасштабного
анализа, функция
![]() декомпозируется на две функции
декомпозируется на две функции![]() и
и![]() :
:
![]() .
.
Таким образом, получили две новые
последовательности,
![]() и
и![]() .
Этот процесс может быть продолжен для
.
Этот процесс может быть продолжен для![]() и функция
и функция![]() (а также и последовательность
(а также и последовательность![]() )
будет представлена совокупностью
коэффициентов
)
будет представлена совокупностью
коэффициентов![]() .
.
Однако вычисления пока зависят от
непрерывных функций
![]() и
и![]() .
Поэтому покажем, как вычисления DTWS могут
быть выполнены с использованием операций
только над дискретными сигналами.
.
Поэтому покажем, как вычисления DTWS могут
быть выполнены с использованием операций
только над дискретными сигналами.
С учетом того, что масштабирующая функция образует базис соответствующего пространства, можно получить:
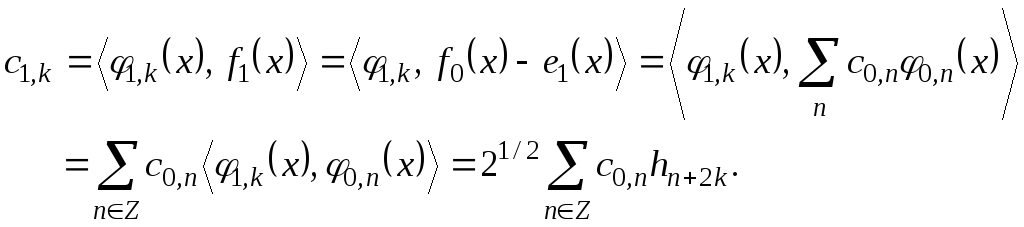 (32)
(32)
Так что оказывается возможным итеративное
вычисление коэффициентов
![]() и
и![]() без непосредственного использования
функций
без непосредственного использования
функций![]() и
и![]() .
По аналогии с (32) можно записать для
произвольного
.
По аналогии с (32) можно записать для
произвольного![]() ,
,
![]() (33)
(33)
![]() (34)
(34)
получив, таким образом, полностью
дискретный процесс декомпозиции.
Последовательности
![]() и
и![]() называются wavelet-фильтрами. Отметим, что
называются wavelet-фильтрами. Отметим, что![]() и
и![]() имеют "половинную" длину по сравнению
с
имеют "половинную" длину по сравнению
с![]() ,
хотя на данном этапе все последовательности
бесконечны. Таким образом, не вводится
избыточность.
,
хотя на данном этапе все последовательности
бесконечны. Таким образом, не вводится
избыточность.
Обратный процесс заключается в получении
![]() из
из![]() и
и![]() :
:
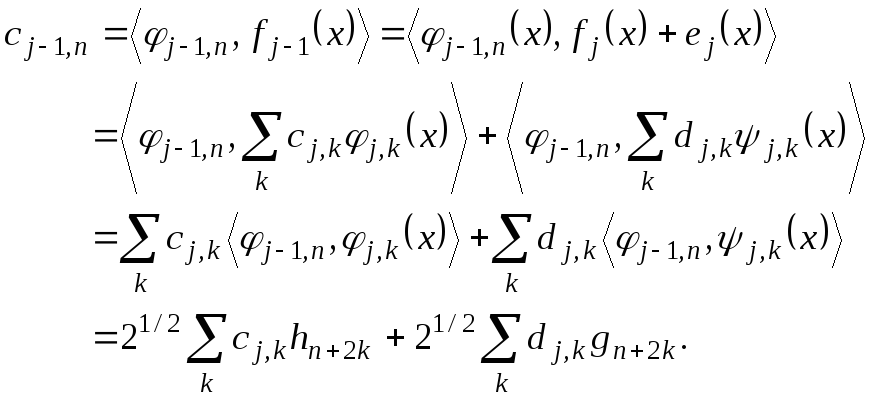 (35)
(35)
Отметим, что в данном случае суммирование
производится по другим переменным по
сравнению с формулами (33) и (34). Длина
последовательности
![]() вдвое больше длины последовательности
вдвое больше длины последовательности![]() или
или![]() .
.
Подставляя (33) и (34) в (35), получаем следующие
ограничения на фильтры
![]() и
и![]() :
:
![]() ,
(36)
,
(36)
![]() ,
(37)
,
(37)
![]() .
(38)
.
(38)
Выражение (36) для временной области эквивалентно выражениям (28) и (32) для частотной. Равенства (38) и (38) уже появлялись ранее, но в менее общей форме.
На практике DTWS должно применяться к сигналам конечной длины. Получившееся преобразование называется "дискретное wavelet-преобразование" (DWT).
Вначале опишем DWT в матричном виде, а затем – на основе банков фильтров, что наиболее часто используется при обработке сигналов.
В обоих случаях мы предполагаем, что
базисные функции
![]() и
и![]() компактно определены. Это автоматически
гарантирует финитность последовательностей
компактно определены. Это автоматически
гарантирует финитность последовательностей![]() и
и![]() .
Далее предположим, что сигнал, подвергаемый
преобразованию, имеет длину
.
Далее предположим, что сигнал, подвергаемый
преобразованию, имеет длину![]() .
.
