Задача 1.

Имеем выборочные данные:

0 5 0 0 0 1 2 1 0 1 0 1 0 2 1 1 1 2 1

1 1 2 0 1 1 0 3 1 1 2 1 2 1 3 0 1 0 3

2 0 1 1 2 0 1 5 0 0 0 2 1 0 2 1 1 2 1

1 1 2 1 0 1 1 3 3 1 2 1 0 0 0 3 0 3 1

0 2 1 1 4 0 0 0 2 1 1 0 2 3 2 0 2 3 2

2 3 0 1 2

Обозначим через варианты признака Х. Из условия видим, что принимает одно из значений 0, 1, 2, 3, 4, 5. Следовательно, Х – дискретная случайная величина. Объем выборки n = 100. Просматривая данные, подсчитываем частоты вариант и записываем в таблицу (графы 2 и 3). Мы предлагаем формировать общую таблицу, которая содержит вспомогательные и итоговые результаты подсчетов по всем пунктам задания. Она заполняется по мере выполнения работы.

Таблица 1.

i	xi	ni			xi ni	xi2 ni	Pi		ni
1	2	3	4	5	6	7	8	9	10	11
0	0	29	0,29	0,29	0	0	0,2923	29,23	29	0.0018
1	1	37	0,37	0,66	37	37	0,3595	35,95	37	0,0307
2	2	21	0,21	0,87	42	84	0,2211	22,11	21	0,0557
3	3	10	0,10	0,97	30	90	0,0906			0,0176
4	4	1	0,01	0,98	4	16	0,0279
5	5	2	0,02	1,00	10	50	0,0068
Σ		100	1,00		123	277	0,9982			0,1058

Вычисляем относительные частоты вариант по формуле (i = 0,1,2,...,5). Результаты вносим в графу 4. Теперь совокупность граф 2 и 3 есть статистический ряд распределения частот, а столбцов 2 и 4 – статистический ряд распределения относительных частот.

Начертим полигон частот, откладывая на горизонтальной оси варианты , а на вертикальной – соответствующие частоты . Затем полученные точки последовательно соединяем отрезками прямых.

Эмпирическая функция распределения определяется формулой , где – сумма частот вариант, меньших х. В статистике она

является аналогом интегральной функции распределения в теории вероятностей. Исходя из таблицы 1 (графа 4), получим:

(чертеж см. на следующей странице).

Вычислим выборочные оценки параметров распределения по формулам:

выборочную среднюю ,

выборочную дисперсию ,

выборочное среднеквадратическое отклонение .

Д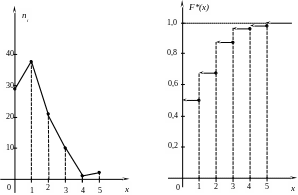 ля этого заполняем графы 5 и 6. Получим: ; ; .

По виду полигона, а также из того, что и почти совпадают, что является признаком распределения Пуассона, выдвинем гипотезу о том, что рассматриваемый признак Х распределен по закону Пуассона , (i = 0, 1, 2, 3, ...), где — математическое ожидание и дисперсия распределения. Положим в нашем случае . Тогда .

Вычисляем теоретические вероятности : ;

; ; ; ; (графа 8).

Вопрос: почему сумма отличается от единицы?

Сравнивая графы 4 и 8, еще раз убеждаемся, что распределение близко к пуассоновскому.

Согласно критерию согласия Пирсона вычисляется статистика

,

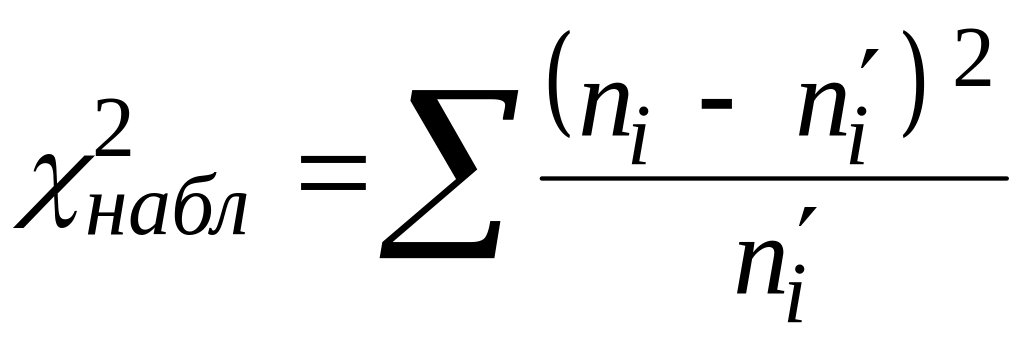где – теоретические (выравнивающие) частоты. Для их вычисления элементы графы 8 умножаем на n = 100 (графа 9). В графу 11 вносим величины 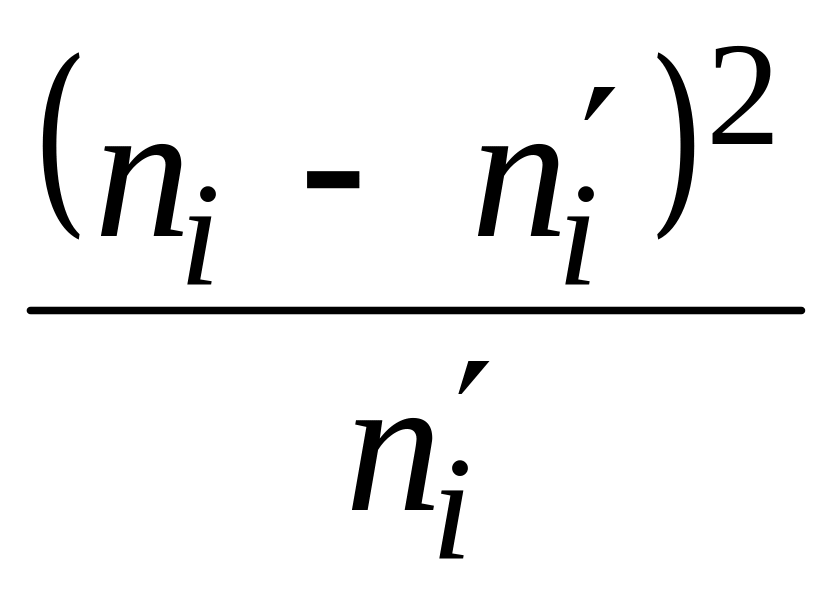. При этом учитываем, что значения вариант, частоты которых меньше 5, надо объединить с соседними вариантами так, чтобы их общая сумма оказалась больше пяти. В нашем случае объединяем последние три варианты, считая при этом, что эмпирическая сумма вариант равна (графа 10), а . Соответственно, в графе 11 считаем общее для них значение . После этого ^(*).

Для отыскания находим число степеней свободы , где k=4 – число групп (учитывая объединение), r=1 – число параметров распределения (один расчетный параметр ). Итак, . По таблице « » при уровне значимости находим . Как видим, . Следовательно, критерий Пирсона позволяет не отвергать гипотезу о распределении Пуассона

для рассматриваемой статистической совокупности.

Замечание. Если наблюдаемое значение статистики окажется больше критического, следует усомниться в правильности выдвинутой гипотезы.