Запишем это бинарное отношение как множество пар:

lllllllllll

П.3. Отношение эквивалентности и фактор множества.

Определение. Бинарное отношение на множестве называется от­ношением эквивалентности, если оно рефлексивно, симметрично и тран­зитивно.

Пример. Отношение равно на множестве - это отношение эквива­лентности.

Определение. Пусть - отношение эквивалентности на множестве , . Классом эквивалентности, порожденным элементом , называ­ется множество всех элементов из множества , находящихся в отноше­нии с элементом .

Класс эквивалентности, порожденный элементом , обозначается: ( по ).

Определение. Совокупность всех классов эквивалентности отноше­ние на множестве называется фактор множества множества по отно­шению эквивалентности .

Обозначается:

Определение. Разбиением множества называется такое семейство его непустых подмножеств, что каждый элемент множества входит в точ­ности в один из членов семейства. Другими словами, разбиением мно­жества называется совокупность его подмножеств , которые об­ладают следующими свойствами:

1. 

2. 

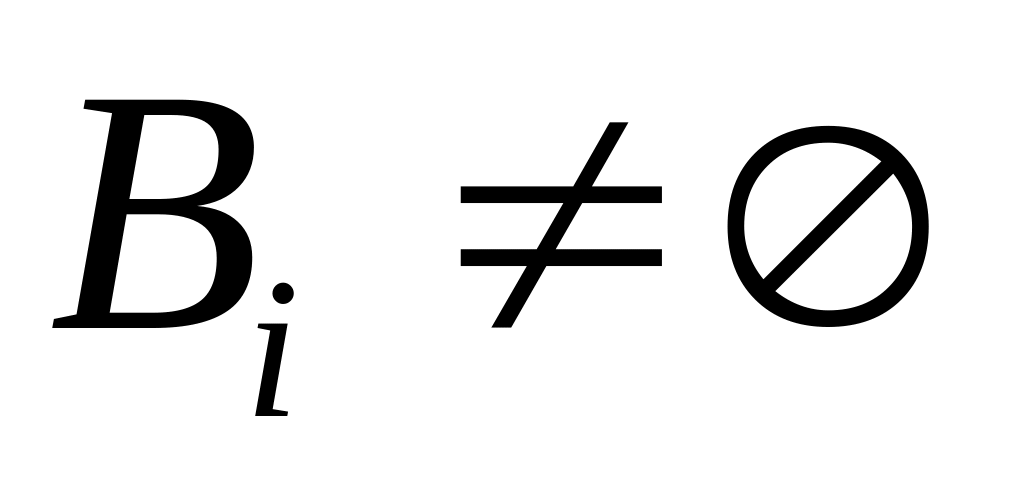
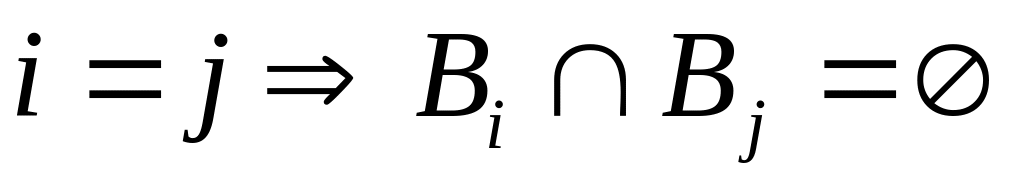
3. , т.е. разбиение множества есть свойство его не­пустых подмножеств, объединение которых совпадает с множеством , пересечение любых двух из них не пусто.

Пример. Пусть дано множество . Будут ли следующие се­мейства множеств разбиением.

1) ; ; - являются разбиением

2) ; - являются разбиением

3) ; - не являются разбиением

Задача. (НИРС)

Пусть имеет элементов. Сколько существует разбиений множе­ства .

Теорема 1. Пусть - отношение эквивалентности на непустом множе­стве , тогда фактор множества является разбиением множества .

Доказательство. Для того, чтобы доказать, что является разбие­нием, нужно проверить, что выполняются три условия:

1. Проверим, что все классы не пусты. Для этого рассмотрим класс экви­валентности, порожденным элементом . , элемент на­ходится в отношении с элементом , т.е. , т.к. - отноше­ние эквивалентности, то оно рефлексивно.

2. Возьмём два разных класса эквивалентности 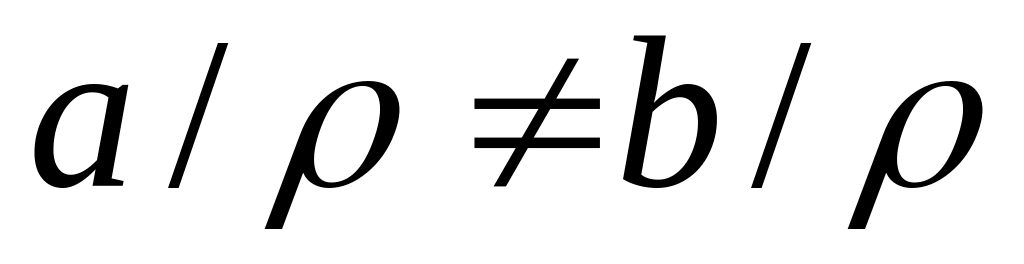. Докажем, что пересечение этих классов пусто: .

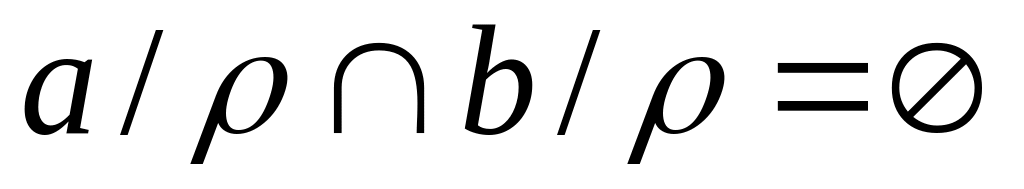Доказательство от противного: предположим, что

Докажем, что классы эквивалентности равны, т.е. .

Пусть

Обратное включение доказывается аналогично.

- противоречие с условием.

Полученное противоречие доказывает нужное утверждение.

3. 

Каждый класс эквивалентности – подмножество множества .

. Докажем обратное включение: .

Итак, фактор множества - это разбиение множества .

Теорема доказана.

Теорема 2. Пусть система множеств - разбиение множества . Определим на множестве отношение . Элемент находится в отно­шении с элементом тогда и только тогда, когда принадлежат одному из множеств : .

Тогда - отношение эквивалентности на множестве и фактор мно­жества .

Доказательство очевидно, следует из определений.

Из теорем 1 и 2 следует, что задать отношение эквивалентности на множестве это тоже самое, что задать разбиение множества .

П.4. Отношение порядка.

Определение. Бинарное отношение на множестве называется от­ношением частичного порядка, если оно рефлексивно, антисимметрично и транзитивно.

Пример. 1. Отношение на множестве - это отношение частич­ного порядка (см пример п.2 Бинарные отношения).

2. Отношение включения на множестве семейства множеств - это от­ношение частичного порядка (см. п. Подмножества).

Определение. Бинарное отношение на множестве называется от­ношением строгого порядка, если оно антирефлексивно, антисиммет­рично и транзитивно.

Например, отношение < на - отношение строгого порядка.

Определение. Отношение частичного порядка на множестве на­зывается отношением линейного порядка, если или , т.е. любые два элемента сравнимы по отношению .

Определение. Отношение строгого порядка на множестве - ли­нейное, если или или .

Пример. 1. Отношение на множестве - это отношение строгого линейного порядка.

2. Отношение на множестве - это отношение частичного линей­ного порядка на .

3. Можно ли определить вид отношения включения на семействе множеств?

Есть множества, которые не сравнимы по отношению включения, на­пример, множество чётных чисел и множество нечётных чисел, поэтому мы не можем утверждать, что любые два множества сравнимы по от­ношению включения, а значит, мы не можем определить вид отношения включения.