Упорядоченные множества.

Определение. Пусть - отношение частичного порядка на множе­стве , тогда упорядоченная пара называется частично упорядочен­ным множеством - это множество с заданным на нём порядком (ч.у.м.)

Определение. Пусть - отношение строгого порядка на множестве . Тогда называется строго упорядоченным множеством - это мно­жество с заданным на нём строгим порядком.

П.5. Функции (отображения).

Пусть , - множества.

Описание. Говорят, что задана функция, определенная на множестве со значениями во множестве , если в силу некоторого закона каж­дому элементу из множества поставили в соответствие единственный элемент во множестве .

или

- область определения ; - область прибытия .

Слова «функция» и «отображение» - синонимы.

Если в силу некоторого закона элементу ставить в соответствие , то пишут: или или .

Определение. Множество всех значений функции , которые она принимает на элементах множества , называется множеством значений функции.

Множество значений функции обозначается: .

Область значений функции обозначается: .

Определение. Графиком функции , определенной на множестве и принимающей значения во множестве называется множество .

Определение. Две функции и равны, если:

1. если они имеют одинаковую область определения, т.е. ;

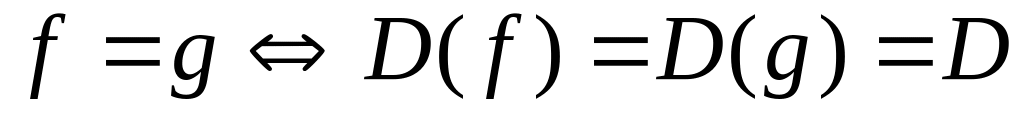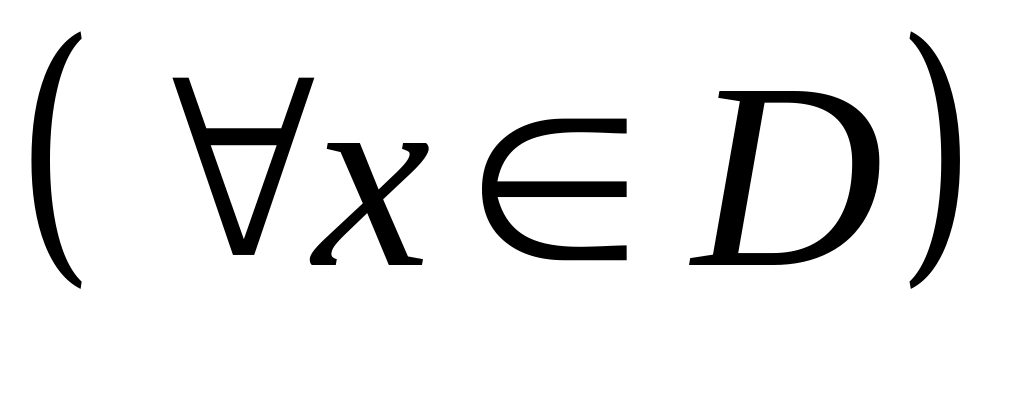2. множества значений этих функций равны .

Пример. Пусть ;

,

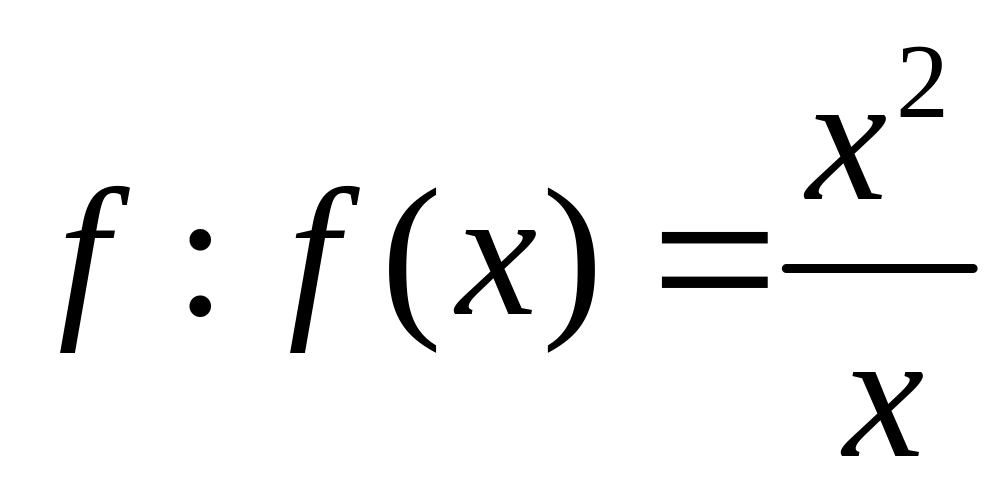Сужение функции.

Определение. Пусть , . Сужением функции на множество называется .

Пример. ;

0

Рассмотрим сужение этой функции.

а) ;

б) ;

в) ;

Сформируем описание функции как отношение.

Определение. Отношение , являющееся подмножеством прямого произведения называется функцией, если:

1)

2)

Другими словами, отношение является функцией, если существует и при том единственное , такое, что находится в отношении с элементом .

Если отношение - функция и находится в отношении с элемен­том , то записывают

Задача. Пользуясь формальным определением функции доказать приведённое выше определение равенства функции.

Виды функций.

Определение. Функция называется инъекцией (инъектив­ным отображением), если она обладает свойством:

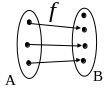
Рис. 1.

Используя закон контрапозиции можно дать другое определение инъекции, равносильное приведённому выше.

Функция называется инъекцией (инъектив­ным отображением), если она обладает свойством:

Определение. Функция называется сюръекцией, если

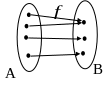
Рис.2.

В чём разница рисунков?

На рисунке 1 к некоторым точкам проведены стрелки. Если к точке проведена стрелка, то только одна. На рисунке 2 к каждой точке множе­ства проведена стрелка. К некоторым точкам множества может быть проведено несколько стрелок.

О пределение. Функция называется биекцией (взаимноодно­значным отображением), если одновременно инъективно и сюръективно.

Задача (УИРС).

Пусть - конечные множества. - биекция.

Что можно сказать про мощность множеств?

Пример. Определить вид следующих функций.

1 . ;

- не является инъекцией,

- сюръекция,

- не является биекцией.

2 . ;

- не является инъекцией,

- не является сюръекцией,

- не является биекцией.

3. ;

- инъекция,

- сюръекция,

- биекция.

4 . ;

- инъекция,

- сюръекция,

- биекция,

Задача.

Пусть - конечные множества. , .

Сколько существует инъекций таких, что ?

Сколько существует сюръекций таких, что ?

Сколько существует биекций таких, что ? Какое условие су­ществования этих функций?