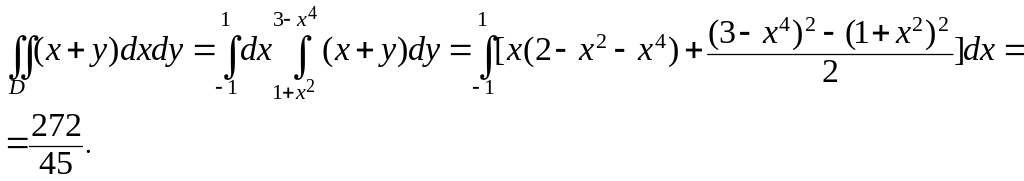Понятие о кратном интеграле Римана.
Простейшим
обобщением интеграла Римана по отрезку
является кратный интеграл, то есть
интеграл от функции
переменных по области
![]() в
в
![]() .
Схема построения интеграла Римана
такая же, как для функции одной переменной.
Область
разбивается на множество малых
подобластей. В каждой из подобластей
выбирается точка, в которой вычисляется
значение функции. Составляется сумма
Римана – сумма произведений полученных
значений функции на меру подобласти.
Такой мерой является площадь подобласти
в случае
.
Схема построения интеграла Римана
такая же, как для функции одной переменной.
Область
разбивается на множество малых
подобластей. В каждой из подобластей
выбирается точка, в которой вычисляется
значение функции. Составляется сумма
Римана – сумма произведений полученных
значений функции на меру подобласти.
Такой мерой является площадь подобласти
в случае
![]() и объем в случае
и объем в случае
![]() .
Меняя разбиения области так, что
подобласти стягиваются в точки, мы
следим за значениями интегральных сумм
Римана. В случае, когда эти суммы имеют
предел, не зависящий ни от способа
разбиения области на подобласти, ни от
способа выбора точек в подобластях, где
вычисляются значения функции в
интегральных суммах, такой предел
называют интегралом Римана соответствующей
кратности по заданной области.
.
Меняя разбиения области так, что
подобласти стягиваются в точки, мы
следим за значениями интегральных сумм
Римана. В случае, когда эти суммы имеют
предел, не зависящий ни от способа
разбиения области на подобласти, ни от
способа выбора точек в подобластях, где
вычисляются значения функции в
интегральных суммах, такой предел
называют интегралом Римана соответствующей
кратности по заданной области.
Вычисляют кратный интеграл Римана, сводя его к последовательности вычислений интегралов Римана по отрезку.
П р и м е р 1. Вычислить
![]() ,
где область
,
где область
![]() – прямоугольник
– прямоугольник
![]() .
Перейдем от двойного интеграла к
повторному, расставив пределы
интегрирования по отрезкам в соответствии
с изменением координат в прямоугольнике.
При этом выбор последовательности
интегралов не имеет значения:
.
Перейдем от двойного интеграла к
повторному, расставив пределы
интегрирования по отрезкам в соответствии
с изменением координат в прямоугольнике.
При этом выбор последовательности
интегралов не имеет значения:
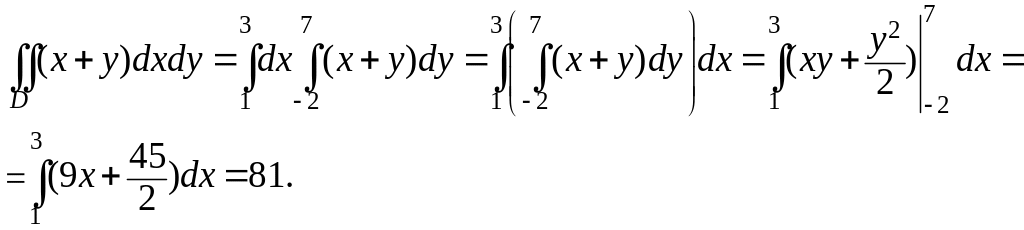
В случае, когда область интегрирования не является прямоугольником, эту область проецируют на одну из координатных осей. Внешний интеграл берут по соответствующей координате. Пределы интегрирования во внутреннем интеграле расставляют в соответствии с уравнениями границ.
П р и м е р 2. Вычислить
,
где
– область, ограниченная кривыми
![]() и
и
![]() .
Точками пересечения двух кривых являются
(1,2) и (-1,2). Проекция области на ось OX
– это отрезок [-1,1]. Следовательно, внешний
интеграл возьмем по переменной
.
Точками пересечения двух кривых являются
(1,2) и (-1,2). Проекция области на ось OX
– это отрезок [-1,1]. Следовательно, внешний
интеграл возьмем по переменной
![]() вдоль
вдоль

этого отрезка.
Пределы интегрирования во внутреннем
интеграле – по переменной
![]() –
зависят от местоположения переменной
и равны: нижний
–
зависят от местоположения переменной
и равны: нижний
![]() ,
верхний
,
верхний
![]() .
Таким образом, получим
.
Таким образом, получим