Звичайні диференціальні рівняння вищих порядків

4. Диференціальні рівняння вищих порядків, які інтегруються в квадратурах, або допускають зниження порядку:

а) .

б) .

в) .

г) .

д) .

5. Лінійні диференціальні рівняння -го порядку.

а) Означення лінійного диференціального рівняння -го порядку. Теорема про існування і єдиність розв’язку задачі Коші

б) Простір розв’язків лінійного однорідного рівняння.

в) Фундаментальна система розв’язків. Визначник Вронського.

г) Формула Остроградського-Ліувілля. [Формула Абеля].

д) Структура загального розв’язку однорідного рівняння.

е) Лінійне однорідне диференціальне рівняння зі сталими коефіцієнтами: характеристичне рівняння, фундаментальна система розв’язків, загальний розв’язок.

є) Структура загального розв’язку неоднорідного рівняння.

ж) Побудова частинного розв’язку неоднорідного диференціального рівняння методом варіації довільних сталих.

з) Побудова частинних розв’язків неоднорідного рівняння зі сталими коефіцієнтами способом невизначених коефіцієнтів.

6. Диференціальні рівняння другого порядку і коливні процеси.

а) Вільні коливання.

б) Вимушені коливання. Явище резонансу.

Дифереціальні рівняння вищих порядків

Рівняння вигляду

, (1)

де – незалежна змінна, – невідома функція, – похідні невідомої функції, – відома дійсна функція дійсних змінних, називається звичайним диференціальним рівнянням -го порядку. Рівняння, у яких , називаються диференціальними рівняннями вищого порядку.

Функція називається розв’язком диференціального рівняння (1), якщо вона разом зі своїми похідними до -го порядку включно перетворює рівняння в тотожність на множині :

для всіх .

Нехай – довільне число з множини , а – довільні дійсні числа.

Відшукання розв’язку рівняння (1), який задовольняє умови

, (2)

називається задачею Коші для рівняння (1), а умови (2) називаються початковими умовами задачі Коші.

Функція , де – довільні дійсні числа, називається загальним розв’язком диференціального рівняння (1), якщо:

1) ця функція є розв’язком рівняння при будь-яких ,

2) сталі можна визначити так, що розв’язок задовольнятиме початкові умови (2).

4. Диференціальні рівняння вищих порядків, які інтегруються в квадратурах або допускають зниження порядку. До таких рівнянь у першу чергу належать наступні рівняння:

а) ,

б) ,

в) ,

г) ,

д) .

а) Рівняння розв’язуються шляхом послідовного кратного інтегрування. Оскільки за означення похідної -го порядку ,

то з рівності дістаємо

Після наступних інтегрувань матимемо рівності:

,

…………………………………………………………………………………..

Після кроків інтегрування отримаємо рівність

,

яка є загальним розв’язком даного рівняння.

Приклад 1. Розв’язати диференціальне рівняння

.

Відповідь:

б) Для інтегрування рівняння уведемо змінну , отримаємо . Переходячи до диференціалів, дістанемо систему

.

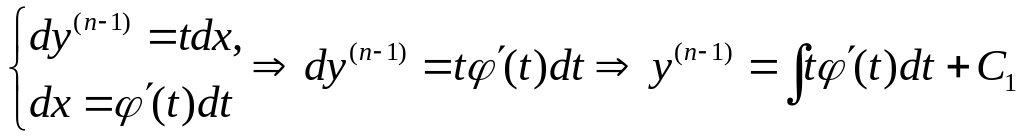Виконуючи послідовно аналогічні дії, будемо мати рівності

…………………………………………………..

Таким чином, загальний розв’язок рівняння б) визначається параметрично функціями:

Приклад 2. Розв’язати рівняння

.

Р о з в ’ я з а н н я. Запишемо рівняння так:

.

Отже, загальний розв’язок рівняння знайдено в параметричному вигляді: , .

в) Понизити порядок диференціального рівняння можна за допомогою підстановки , де – нова невідома функція. Оскільки , то приходимо до диференціального рівняння першого порядку з відокремленими змінними, яке інтегрується у квадратурах:

Якщо – загальний розв’язок цього рівняння, то повертаючись до підстановки дістанемо рівняння вигляду а)

.

Звідси маємо

.

Якщо загальний інтеграл здобутого рівняння, то дістаємо рівняння -го порядку .

Приклад 3. а) Розв’язати рівняння

,

Відповідь:

б) Понизити порядок рівняння

.

Відповідь: .

г) Порядок диференціального рівняння понижується уведенням невідомої функції . Підставивши функцію та її похідну у рівняння, матимемо диференціальне рівняння першого порядку . Якщо це рівняння інтегрується у квадратурах і – його загальний розв’язок, то з рівняння знаходимо загальний розв’язок рівняння г):

Якщо загальний інтеграл здобутого рівняння, то дістаємо рівняння першого порядку .

Приклад 4а) Розв’язати рівняння:

.

Р о з в ’ я з а н н я. Спочатку дістаємо однорідне рівняння

,

інтегруючи яке матимемо

Звідси – загальний розв’язок даного рівняння, знайдений у квадратурах. Застосовуючи інтегрування частинами знаходимо інтеграл

Відповідь:

Приклад 4б) Розв’язати задачу Коші

.

Відповідь: .

г) Для пониження порядку диференціального рівняння уведемо підстановку , у якій нова невідома функція є функцією змінної . Тоді і рівняння запишеться так:

.

Якщо отримане диференціальне рівняння першого порядку інтегрується у квадратурах і – його загальний розв’язок, то дістанемо диференціальне рівняння з відокремленими змінними , яке інтегрується у квадратурах.

Якщо загальний інтеграл здобутого рівняння, то дістаємо рівняння першого порядку .

Приклад 5. Понизити порядок диференціального рівняння

Р о з в ’ я з а н н я. Виконуючи вказану заміну, дістанемо однорідне рівняння

. Якщо , то прийдемо до рівняння

Звідси маємо , а . Тому – диференціальне рівняння першого порядку, що не розв’язане відносно похідної.