8.Група рухів (переміщень) площини. Застосування рухів до розв’язування задач. Приклади.

Озн: Рухом або переміщенням площини наз перетворення площини при якому зберігається відстань між будь-якими 2 точками. (1)

Властивості руху:

1.При русі зберігається відношення лежати між(тобто одна точка завжди лежить між двома іншими) .

2.При русі зберігається просте відношення 2-х точок. .

3.При русі пряма переходить в пряму, промінь в промінь, коло-коло, кут-кут, відрізок-відрізок. Властивість випливає з перших двох.

4.При русі ортонормований репер , так що т.М^/, яка є образом т.М, відносно R^/ має такі ж координати, як і т.М відносно R.

5.Множина всіх рухів площини утворює групу.

Під формулами руху будемо розуміти співвідношення між (координатами) точками образа і прообраза ортонорм. репера R. f(R)=R^/, f(M)=M^/ .Розглянемо т.М^/ і репери R і R^/, маємо перетворення ортонормованого репера. R:М(х,у), R^/:М^/(х,у), R^/М^/(х^/,у^/). Запишемо формулу перетворення ортонормованого репера R: (3) . Розглянемо т.М і М^/, R, a R^/-не беремо. Формули (3) виражають відношення між координатами точок М і М^/(прообразу і образу) при русі Ф при одному і тому ж реперу R. Це означає, що формули (3) і є одночасно формулами аналітичного задання руху.

Якщо то рух наз. першого роду, якщо то маємо рух другого роду.

Озн: Рух першого роду-це рух при якому геометрична фігура переходить у однаково орієнтовану фігуру.

Озн: Рух при, якому орієнтація фігури міняється на протилежну наз. другого роду.

Зауваж: Множина рухів 1-го роду утв. групу, а множина рухів 2-го роду групу не утворюють(бо композиція двох ручів 2-го роду є рухом 1-го роду).

Озн: Дві фігури Ф₁ і Ф₂ наз рівними, якщо існує рух (переміщення), яке переводить одну фігуру Ф₁ у Ф₂.

Доведіть, що це афінне перетворення:

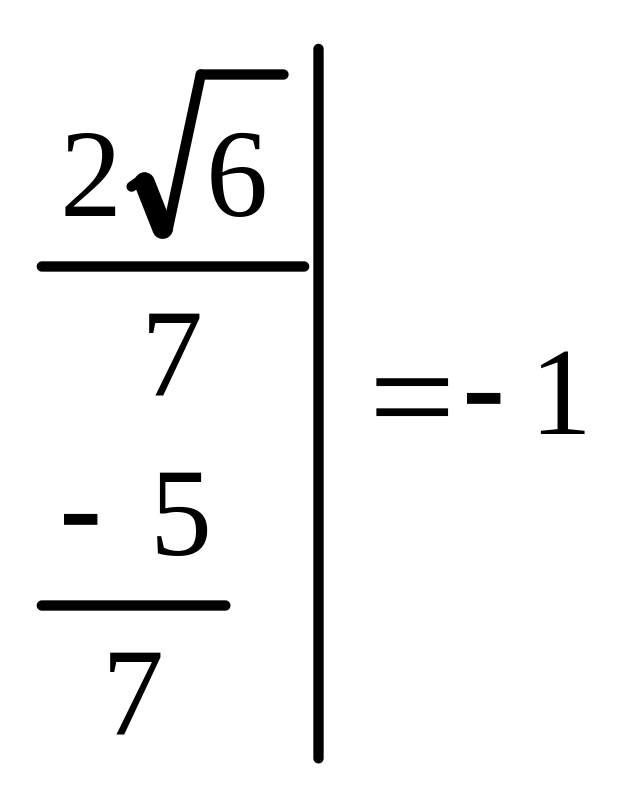, отже, це переміщення другого роду.

9. Класифікація рухів. Розклад рухів у добуток осьових симетрій.

Класифікація рухів:

1.Паралельне перенесення. Нехай на площині дано вектор і довільну точку М(х,у).

Озн: Паралельним перенесенням на наз таке перетворення площині при якому так, що = . Позначається Т . Знайдемо формули аналітичного задання перенесення ММ^/=(х^/-х, у^/-у), М^/=(х^/,у^/).

(1) (2).

Паралельне перенесення це рух другого роду. Паралельне перенесення на є одиничним перенесенням. При паралельному перенесенні і нерухомих точок немає. При паралельному перенесенні пряма переходить у паралельну пряму. Пряма паралельна до переходить сама в себе. Множина всіх паралельних перенесень площини утв. групу, яка є підгрупою групи першого роду.

2.Поворот площини. Нехай на площині задано т.М і . Озн: Поворотом площини навколо т.М₀ на наз. таке перетворення площини при якому т.М т.М^/ так, що відстань і . M₀-центр повороту, -кут повороту. Позначається .

- формули аналітичного задання повороту.

Якщо ж за центр повороту прийняти довільну точку то формули повороту набувають такого вигляду:

- формули повороту навколо точки.

Властивості:

1.Поворот площини є рух, причому рух 1-го роду.

2.При повороті пряма переходить у пряму, коло у рівне коло, кут у рівний кут, відрізок у рівний відрізок.

3.множина всіх поворотів площини утв. групу, яка є підгрупою рухів групи рухів 1-го роду.

Поворот на кут 180⁰ наз. центральною симетрією, якщо у формулах повороту прийняти то позн. центр. симетрію будемо так z₀. - відносно початку координат.

3.Осьова симетрія. Розглянемо на площ. деяку пряму і т.М.

Озн: Осьовою симетрією з віссю l, або симетрією відносно l наз таке перетворення площини, при якому т.М переходить у М^/, так що відрізок ММ^/ і т. перетину М₀ з віссю l ділиться пополам. Позначається- . Знайдемо формули осьової симетрії, прийнявши за вісь ох або оу ортон. системи репера. OX : ОУ:

Зауваження:

1.Що осьова симетрія є рух, при чому рух другого роду.

2.Оскільки рух 2-го роду не утв. групу, то множ. осьових симетрій не утв. групу.

3.При осьовій симетрії точки осі є нерухомими.

4.Пряма перпендикулярна осі переходить сама в себе.

4.Ковзна (коса) симетрія.

Озн: Ковзною симетрією наз перетворення площини, яке є композицією осьової симетрії і паралельного перенесення на вектор паралельний до осі симетрії . Ковзна симетрія є композицією двох рухів, отже це рух другого роду.

Знайдемо формулу ковзної симетрії

прийнявши спочатку вісь: ОХ: . М(х,у), . Запишемо формули осьової симетрії

Якщо за вісь симетрії взяти вісь ОУ: .

Розклад рухів, добуток (композиція) осьової симетрії.

Теорема 1. Добуток двох осьових симетрій відносно осей, що перетинаються є поворот навколо токи перетину осей симетрії на кут повороту, що = подвійному куту між осями симетрії і навпаки. Всякий поворот можна розкласти у вигляді добутку композиції двох осьових симетрій відносно осей, що перетинаються в т. повороту і кутом між ними, що = половині куту повороту.

Теорема 2. Добуток двох осьових симетрій відносно двох паралельних осей є паралельне перенесення на вектор довжина, якого = подвійній відстані між осями симетрії, і навпаки всяке паралельне перенесення на вектор можна представити у вигляді композиції двох осьових симетрій з паралельними осями відстань між якими = половині довжини вектора.

Теорема 3. Всякий рух можна розкласти у вигляді композиції не більше 3-осьових симетрій.

Якщо рух є осьовою симетрією то твердження теореми істинне.

Якщо рух є поворотом то за Т.1. це є композиція з осями, що перетинаються.

Якщо рух є паралельне перенесення то за Т.2 паралельне осі.

Якщо рух є ковзна симетрія, то твердження теореми істинне і вона розкл. у добуток комп. 3-осьових симетрій.