Билет№3

1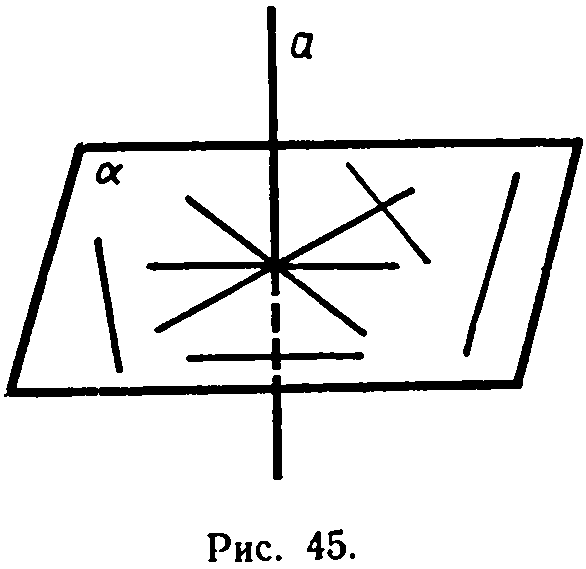 ) Параллельные прямые, перпендикулярные к плоскости.

Определение. Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости.

Перпендикулярность прямой a и плоскости ά обозначается так: . Говорят также, что плоскость ά перпендикулярна к прямой а.

Если прямая a перпендикулярна к плоскости ά, то она пере­секает эту плоскость. В самом деле, если бы прямая a не пере­секала плоскость ά, то она или лежала бы в этой плоскости, или была бы параллельна ей. Но тогда в плоскости а имелись бы прямые, не перпендикулярные к прямой а, например прямые, параллельные ей, что противоречит определению перпендикуляр­ности прямой и плоскости. Значит, прямая a пересекает плос­кость ά.

На рисунке изображена прямая а, перпендикулярная

к плоскости ά.

Окружающая нас обстановка дает много примеров, ил­люстрирующих перпендикулярность прямой и плоскости. Не­покосившийся телеграфный столб стоит прямо, т. е. перпенди­кулярно к плоскости земли. Так же расположены колонны здания по отношению к плоскости фундамента, линии пересечения стен по отношению к плоскости пола и т. д.

Докажем две теоремы, в которых устанавливается связь между параллельностью прямых и их перпендикулярностью

к плоскости.

Теорема

Если одна из двух параллельных прямых перпендикулярна к плоскости, то и другая прямая перпен­дикулярна к этой плоскости.

Д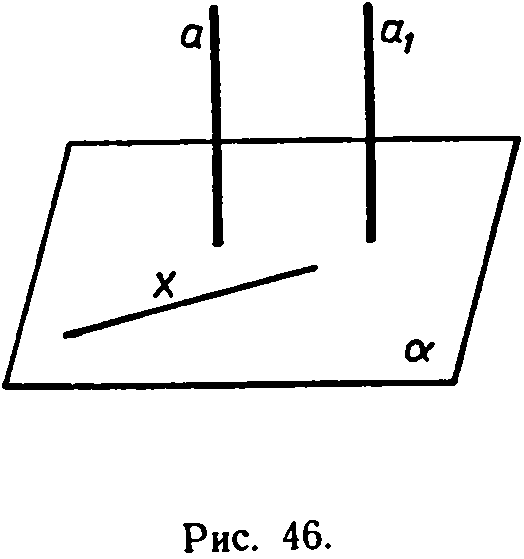 оказательство

Рассмотрим две параллельные прямые а и а₁ и плоскость ά, такую, что а ά. Докажем, что и а₁ ά.

Проведем какую-нибудь прямую х в плоскости ά. Так как а ά, то а х. По лемме о перпендикулярности двух параллельных прямых к третьей а₁ х. Таким образом, прямая а₁ перпендикулярна к любой прямой, лежащей в плоскости ά, т. е. Теорема доказана.

Докажем обратную теорему.

Теорема

Если две прямые перпендикулярны к плоскости, то они параллельны.

Доказательство

Рассмотрим прямые а и b, перпенди­кулярные к плоскости ά. Докажем, что а||b.

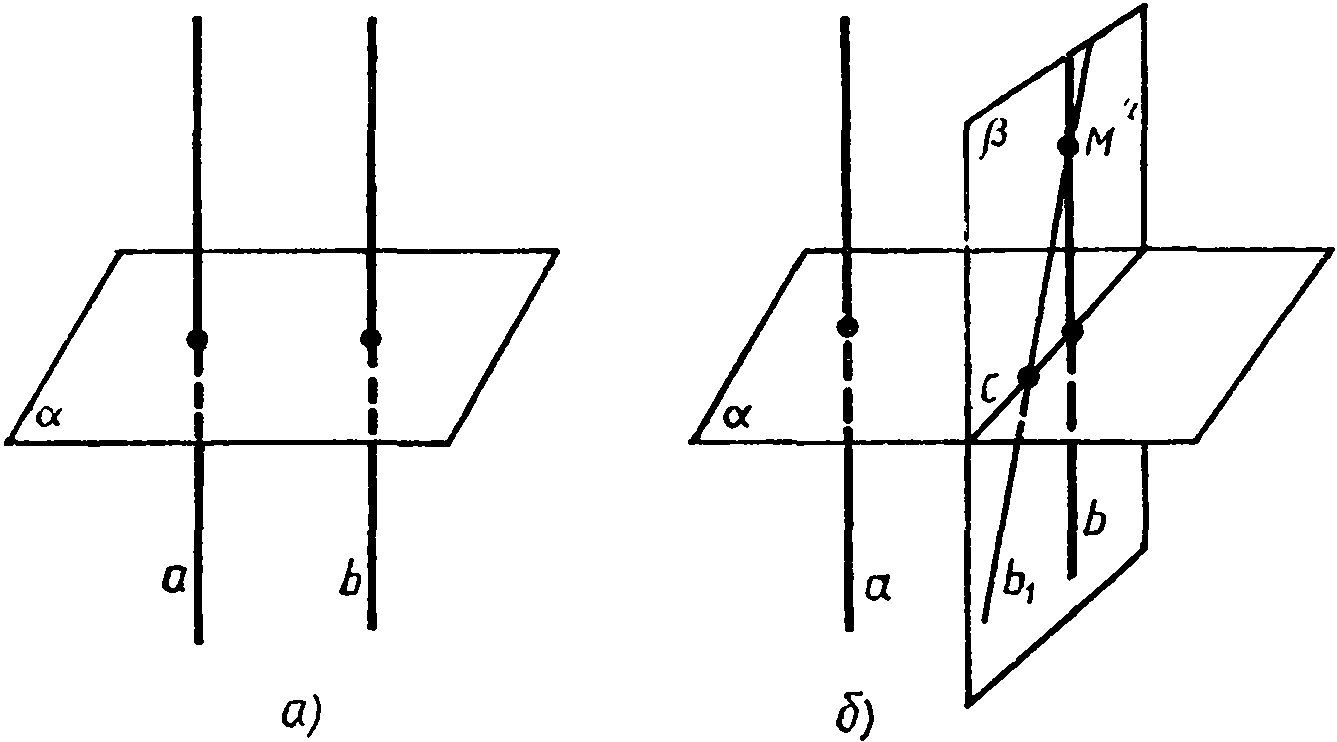
Через какую-нибудь точку М прямой b проведем прямую b₁, параллельную прямой а. По предыдущей теореме ά. Дока­жем, что прямая b₁ совпадает с прямой b. Тем самым будет доказано, что а||b. Допустим, что прямые b и b₁ не совпадают. Тогда в плоскости β, содержащей прямые b и b₁, через точку М проходят две прямые, перпендикулярные к прямой с, по которой пересекаются плоскости ά и β. Но это невозможно, следовательно, а||b.

Теорема доказана.

2) Пирамида. Рассмотрим многоугольник А₁А₂...А_n и точку Р, не лежащую в плоскости этого многоугольника. Соединив точку Р отрезками с вершинами многоугольника, получим п треуголь­н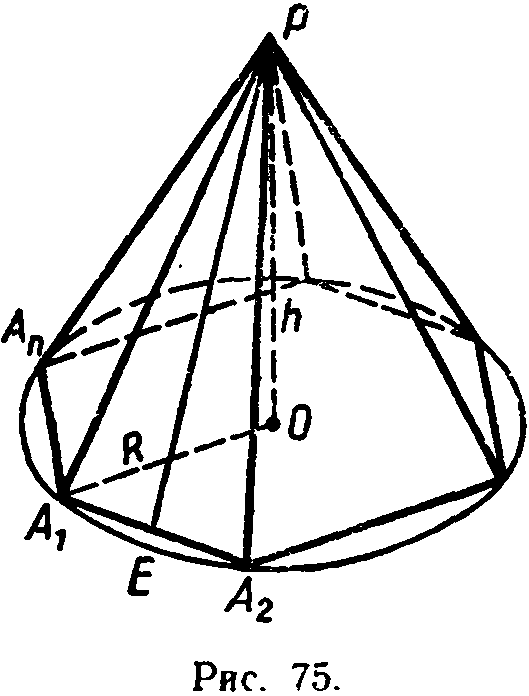 иков:

РА₁А₂, РА₂А₃, ..., РА_пА₁. (1)

Многогранник, составленный из n-угольника А₁А₂...А_n и n тре­угольников (1), называется пирамидой. Многоугольник А₁А₂...А_n

называется основанием, а треугольники (1) — боковыми гранями пирамиды. Точка Р называется вершиной пирамиды, а отрезки РА₁, РА₂, ..., РА_n — ее боковыми ребрами. Пирамиду с основа­нием А₁А₂...А_n и вершиной Р обозначают так: РА₁А₂...А_n— и называют n-угольной пирамидой. Треуголь­ная пирамида — это тетраэдр.

Перпендикуляр, проведенный из вершины пирамиды к плос­кости основания, называется высотой пирамиды. На рисунке отрезок РО — высота пирамиды.

Площадью полной поверхности пирамиды называется сумма площадей всех ее граней (т. е. основания и боковых граней), а площадью боковой поверхности пирамиды — сумма площадей ее боковых граней. Очевидно, что

Sполн=Sбок+Sосн (2)

Правильная пирамида. Пирамида называется правильной, если ее основание — правильный многоугольник, а отрезок, со­единяющий вершину пирамиды с центром основания, является ее высотой.

Докажем, что вес боковые ребра правильной пирамиды рав­ны, а боковые грани являются равными равнобедренными тре­угольниками.

Рассмотрим правильную пирамиду РА₁А₂...А_n. Сна­чала докажем, что все боковые ребра этой пирамиды равны.

Любое боковое ребро представляет собой гипотенузу прямоугольного тре­угольника, одним катетом которого служит высота РО пирамиды, а дру­гим — радиус описанной около основа­ния окружности (например, боковое ребро РА₁ — гипотенуза треугольни­ка ОРА₁, в котором ОР = Н, ОА₁=R). По теореме Пифагора любое боковое ребро равно , поэтому РА₁=PA₂ = ... = PA_n.

Мы доказали, что боковые ребра правильной пирамиды PA₁A₂...A_n рав­ны друг другу, поэтому боковые гра­ни — равнобедренные треугольники.

Основания этих треугольников также равны друг другу, так как А₁А₁…А_n — правильный многоугольник. Следовательно, бо­ковые грани равны по третьему признаку равенства треуголь­ников, что и тре0овалось доказать.

Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой. На рисунке отрезок РЕ — одна из апофем. Ясно, что все апофемы правильной пирамиды равны друг другу.

Докажем теорему о площади боковой поверхности правиль­ной пирамиды.

Теорема

Площадь боковой поверхности правильной пи­рамиды равна половине произведения периметра основания на апофему.

Доказательство

Боковые грани правильной пирами­ды - равные равнобедренные треугольники, основания кото­рых — стороны основания пирамиды, а высоты равны апофеме. Площадь S боковой поверхности пирамиды равна сумме произ­ведений сторон основания на половину апофемы d. Вынося множитель

0,5d за скобки, получим в скобках сумму сторон основания пирамиды, т. е. его периметр.

Теорема доказана