
- •1) Понятие вектора,модуль,коллинеарность и компланарность векторов.Геометрическое и экономическое понятие
- •2) Действие над векторами.Правило параллелограмма и многоугольника
- •3) Координаты вектора,действие над ними,заданными координатам
- •4) Скалярное произведение вектора.Угол между векторами
- •5) Условие параллельности и перпендикулярности векторов
- •6 ) Уравнение прямой на плоскости
- •7) Уравнение прямой в пространстве
- •8) Взаимное расположение прямых,угол между ними.Условие параллельности и перпендикулярност
- •9) Уравнение плоскости,частные случаи общего уравнения плоскости
- •10) Угол между плоскостями.Условие параллельности и перпендикулярности
- •11) Определители и их свойства
- •12) Вычисление определителя
- •13) Решение систем линейных уравнений методом Крамера
- •14) Метод Гаусса
- •15) Матрицы и действия над ними
- •16, 17)) Обратная матрица
- •19) Ранг матриц
- •20) Понятие функции
- •21) Область определения,четность,монотонность
- •22) Понятие предела,бесконечно малые величины и их свойства
- •23) Основные теоремы о пределах
- •24) Виды неопределенности
- •25) Первый замечательный предел
- •26) Второй замечательный предел
- •27) Задачи приводящие к понятию производной
- •28) Производная и ее смысл
- •29) Уравнение касательной
- •30) Основные правила дифференцирования
- •31) Производные тригонометрических функций
- •32) Производные обратных тригонометрических функцй
- •33) Производная логарифмической функции
- •34) Производная сложной функции
- •35) Производная степенной функции
- •36) Производная неявной функции
- •37) Производная высших порядков
- •38) Диф функции
- •39) Приложение дифференциала
- •40) Теорема Лагранджа
- •41) Теорема Роля
- •42) Правило Лопиталя
- •43) Теорема ферма
- •44) Монотонность функции на интервале
- •45) Условие существования экстренума
- •46) Выпуклость и вогнутость функции
- •47) Асимптоты графика функции
- •48) Исследование функции построение графика с помощью производной. Исследование функции с помощью производной
- •49) Исследование функции с помощью производной
- •31) Производные тригонометрических функций
45) Условие существования экстренума
Экстре́мум
(лат. extremum —
крайний) в математике — максимальное
или минимальное
значение функции
на заданном множестве.
Точка, в которой достигается экстремум,
называется точкой
экстремума.
Соответственно, если достигается
минимум — точка экстремума называется
точкой
минимума,
а если максимум — точкой
максимума.
В математическом
анализе
выделяют также понятие локальный
экстремум (соответственно минимум или
максимум).Пусть
дана функция
![]() и
и
![]() —
внутренняя точка области определения
f.
Тогдаx0
называется точкой локального максимума
функции f,
если существует проколотая окрестность
—
внутренняя точка области определения
f.
Тогдаx0
называется точкой локального максимума
функции f,
если существует проколотая окрестность
![]() такая,
что
такая,
что
![]() x0
называется точкой локального минимума
функции f,
если существует проколотая окрестность
такая,
что
x0
называется точкой локального минимума
функции f,
если существует проколотая окрестность
такая,
что
![]() Если
неравенства выше строгие, то x0
называется точкой строгого локального
максимума или минимума соответственно.x0
называется точкой абсолютного
(глобального) максимума, если
Если
неравенства выше строгие, то x0
называется точкой строгого локального
максимума или минимума соответственно.x0
называется точкой абсолютного
(глобального) максимума, если
![]() x0
называется точкой абсолютного минимума,
если
x0
называется точкой абсолютного минимума,
если
![]() Значение
функции f(x0)
называют (строгим) (локальным) максимумом
или минимумом в зависимости от ситуации.
Точки, являющиеся точками (локального)
максимума или минимума, называются
точками (локального) экстремума
Значение
функции f(x0)
называют (строгим) (локальным) максимумом
или минимумом в зависимости от ситуации.
Точки, являющиеся точками (локального)
максимума или минимума, называются
точками (локального) экстремума
46) Выпуклость и вогнутость функции
Выпуклость
и вогнутость свойство графика функции
у
= f
(x)
(кривой), заключающееся в том, что каждая
дуга кривой лежит не выше (не ниже) своей
хорды; в первом случае график функции
f
(x)
обращён выпуклостью книзу (вогнутостью
кверху) и сама функция называется
выпуклой (рис.
1,
а), во втором — график обращён вогнутостью
книзу (выпуклостью кверху) и функция
называется вогнутой (рис.
1,
б). Если существуют производные f
'(x)
и f
"(х),
то первый случай имеет место при условии,
что f
"(x)
≥ 0, а второй при f
"(x)
≤ 0 (во всех точках рассматриваемого
промежутка). Выпуклость (книзу) можно
охарактеризовать также тем, что дуга
кривой лежит не ниже касательной, в
окрестности любой своей точки (рис.
2,
a), а вогнутость (книзу) — тем, что дуга
кривой лежит не выше касательной (рис.
2,
б). Аналогично определяются В. и в.
поверхности.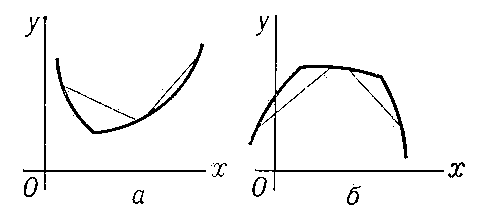 Рис.
1 к ст. Выпуклость и вогнутость.
Рис.
1 к ст. Выпуклость и вогнутость.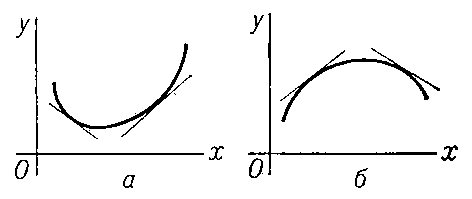
47) Асимптоты графика функции
Назовём
асимптотами
прямые линии, к которым неограниченно
приближается график функции, когда
точка графика неограниченно удаляется
от начала координат. В зависимости от
поведения аргумента при этом, различаются
два вида асимптот: вертикальные и
наклонные. Определение
7.1
Вертикальной
асимптотой
графика функции
![]() называется
вертикальная прямая
называется
вертикальная прямая
![]() ,
если
,
если
![]() или
или
![]() при
каком-либо из условий:
при
каком-либо из условий:
![]() ,
,
![]() ,
,
![]() .
Заметим, что мы при этом не требуем,
чтобы точка
.
Заметим, что мы при этом не требуем,
чтобы точка
![]() принадлежала
области определения функции
принадлежала
области определения функции
![]() ,
однако она должна быть определена по
крайней мере в какой-либо из односторонних
окрестностей этой точки:
,
однако она должна быть определена по
крайней мере в какой-либо из односторонних
окрестностей этой точки:
![]() или
или
![]() ,
где
,
где
![]() .
Пример
7.1
Рассмотрим функцию
.
Пример
7.1
Рассмотрим функцию
![]() .
График
имеет
вертикальную асимптоту
.
График
имеет
вертикальную асимптоту
![]() ,
поскольку при
,
поскольку при
![]() выполняется
условие
выполняется
условие
![]() ,
а также при
,
а также при
![]() выполняется
условие
выполняется
условие
![]() .
.
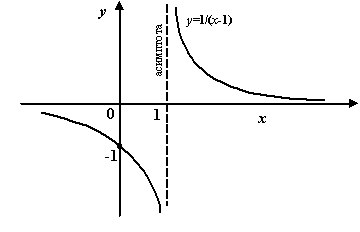
Рис.7.1.Вертикальная
асимптота функции
![]()
Пример
7.2
Рассмотрим функцию
![]() .
Её график имеет вертикальную асимптоту
.
Её график имеет вертикальную асимптоту
![]() ,
так как
,
так как
![]() при
при
![]() .
То, что при
.
То, что при
![]() функция
не
стремится к бесконечности, для наличия
асимптоты неважно: для того, чтобы прямая
являлась
вертикальной асимптотой, достаточно,
чтобы график приближался к ней хотя бы
с одной стороны. (К слову сказать,
функция
не
стремится к бесконечности, для наличия
асимптоты неважно: для того, чтобы прямая
являлась
вертикальной асимптотой, достаточно,
чтобы график приближался к ней хотя бы
с одной стороны. (К слову сказать,
![]() при
.)
при
.)
![]() Рис.7.2.Вертикальная
асимптота функции
Рис.7.2.Вертикальная
асимптота функции
Пример
7.3
Рассмотрим функцю
![]() .
Прямая
является
вертикальной асимптотой графика
,
так как
при
.
Заметим, что слева от точки
функция
вообще не определена.
.
Прямая
является
вертикальной асимптотой графика
,
так как
при
.
Заметим, что слева от точки
функция
вообще не определена.
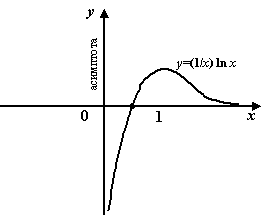 Рис.7.3.Вертикальная
асимптота функции
Пример
7.4
График функции
Рис.7.3.Вертикальная
асимптота функции
Пример
7.4
График функции
![]() не
имеет при
вертикальной
асимптоты, так как
--
ограниченная (числом 1) и, следовательно,
локально ограниченная при
не
имеет при
вертикальной
асимптоты, так как
--
ограниченная (числом 1) и, следовательно,
локально ограниченная при
![]() и
не стремящаяся к бесконечности функция.
Хотя аргумент синуса -- функция
и
не стремящаяся к бесконечности функция.
Хотя аргумент синуса -- функция
![]() --
имеет вертикальную асимптоту
.
--
имеет вертикальную асимптоту
.
 Рис.7.4.График
функции
не
имеет вертикальной асимптоты Пример
7.5
Прямая
не
является вертикальной асимптотой
графика функции
Рис.7.4.График
функции
не
имеет вертикальной асимптоты Пример
7.5
Прямая
не
является вертикальной асимптотой
графика функции
![]() ,
поскольку здесь нельзя утверждать, что
при
или
функция
стремится к бесконечности. При некоторых
малых значениях
,
поскольку здесь нельзя утверждать, что
при
или
функция
стремится к бесконечности. При некоторых
малых значениях
![]() значения
значения
![]() могут
быть как угодно велики, однако при других
малых
функция
обращается в 0: так, при
могут
быть как угодно велики, однако при других
малых
функция
обращается в 0: так, при
![]() (
(
![]() )
значения функции равны
)
значения функции равны
![]() и
стремятся к бесконечности при
и
стремятся к бесконечности при
![]() ,
а при всех
,
а при всех
![]() вида
вида
![]() (
)
значения функции равны 0. В то же время
как те, так и другие точки
при
увеличении
попадают
всё ближе и ближе к точке 0. Значит,
функция
не
является бесконечно большой при
(
)
значения функции равны 0. В то же время
как те, так и другие точки
при
увеличении
попадают
всё ближе и ближе к точке 0. Значит,
функция
не
является бесконечно большой при
![]() ,
и прямая
--
не асимптота.
,
и прямая
--
не асимптота.
 Рис.7.5.График
функции
не
имеет вертикальной асимптоты
Рис.7.5.График
функции
не
имеет вертикальной асимптоты
Итак,
для нахождения вертикальных асимптот
графика данной функции нужно исследовать
точки разрыва функции и точки, лежащие
на границах области определения функции,
и выяснить, при приближении аргумента
к каким из этих точек значения функции
стремятся к бесконечности. Определение
7.2
Наклонной
асимптотой
графика функции
при
![]() называется
прямая
называется
прямая
![]() ,
если выполнены два условия:
1) некоторый
луч
,
если выполнены два условия:
1) некоторый
луч
![]() целиком
содержится в
целиком
содержится в
![]() ;
2) расстояние по вертикали между
графиком и прямой стремится к 0 при
:
;
2) расстояние по вертикали между
графиком и прямой стремится к 0 при
:
|
|
Наклонной
асимптотой
графика функции
при
![]() называется
прямая
,
если
1) некоторый луч
называется
прямая
,
если
1) некоторый луч
![]() целиком
содержится в
;
2) расстояние по вертикали между
графиком и прямой стремится к 0 при
:
целиком
содержится в
;
2) расстояние по вертикали между
графиком и прямой стремится к 0 при
:
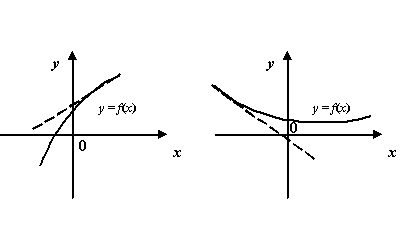 Рис.7.6.Графики
функций, имеющие наклонные асимптоты
при
и
при
Рис.7.6.Графики
функций, имеющие наклонные асимптоты
при
и
при
