2.2.5. Использование метода линейного программирования

Поиск оптимальных плановых решений в АСУ можно свести к двум основным постановкам задач:

1. получение запланированного эффекта при минимуме за­трат;

2. получение максимального эффекта при использовании за­данных организацией ресурсов.

Механизм экономических отношений описывается целым рядом взаимосвязанных показателей: товарооборот, рентабель­ность, избытки обращения, ассортимент товаров, площадь торго­вых залов и подсобных помещений, количество квалифициро­ванных работников, виды оборудования, товарные запасы, сис­тема обработки, система обработки документов, форма обслужи­вания потребителей и т. д.

На значение этих показателей влияют такие факторы как ритмичность, частота и объемы выпуска продукции, поставка ее заказчикам, ассортимент и качество продукции, наличие и ис­правность оборудования, количество персонала и т. д.

Все экономические показатели и факторы можно разделить на:

• неуправляемые (z_i,z₂,-,Z_i,-,Z_m)\

• управляемые (x_l,x₂,--;Xj,...,x_n).

На этом основании целевую функцию можно записать в виде уравнения этих показателей с критерием оптимальности (extre-mum).

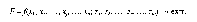
Постановка задачи завершается переводом задачи планиро­вания с языка экономики на язык математики. Этот процесс свя­зан с построением одного или нескольких математических урав­нений или неравенств, которые в совокупности описывают функ­циональные связи критерия оптимальности с показателями ресурсов, факторами и неизвестными значениями управляемых показателей. Такая запись экономической задачи является эконо­мико-математической.

Для представления экономической постановки задачи в виде математической модели линейного программирования необходи­мо целевую функцию представить в виде линейной формы, а связь с ограниченными ресурсами описать с помощью линейных уравнений или неравенств. Кроме того, вводится дополнительное ограничение — значения переменных не должны быть отрица­тельны, т.е. x₁>0,x₂>0,...,Xj>0,...,x_n>0. В целом экономи­ко-математическая формулировка и модель общей задачи линей­ного программирования (ОЗЛП) имеют следующий вид: найти max(min) линейной целевой функции:

при условиях ограничении:

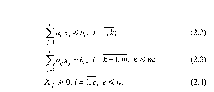
ay, bj, Cj—заданные постоянные величины.

Стандартной задачей линейного программирования назы­вают задачу, которая состоит в определении максимального (ми­нимального) значения целевой функций (2.1), при выполнении условия (2.2) и (2.4), где к = 0 и е = п.

Канонической (или основной) задачей линейного программи­рования называют задачу, которая состоит в определении макси­мального (минимального) значения целой функции при выполне­нии условий (2.3) и (2.4).

Совокупность чисел Зс = (д:₁,А"2,...,jc„), удовлетворяющих ог­раничениям, называется допустимым решением (или планом).

План х* = (х₁*, х₂*,х_п*), при котором целевая функция за­дачи принимает max(min), называется оптимальным.

В случае, когда требуется найти min функции F(x) =

= (с,л-, +с₂х₂ +... + с_пх_п), можно перейти к нахождению max функции

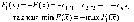
Ограничение — неравенство исходной ЗИП, имеющее вид «<», преобразуется в ограничение равенства с добавлением ле­вой части дополнительной неотрицательной переменной. Огра­ничение-неравенство вида «>» преобразуется в ограничение-ра­венство вычитанием из левой части дополнительной неотрица­тельной переменной.

Если ограничение задачи отражает наличие и равенство про­изводственных ресурсов, то значение дополнительной перемен­ной в плане задачи, записанной в форме основной, равно объему неиспользуемого соответствующего ресурса.

Запишем в ОЗЛП ограничения (2.3) в векторной форме.

Х,А| + Х₂А₂ + ...+ Х_пА_п = В, (2.5)

где A\,Ai,...,A„ и В m-мерные векторы-столбцы, составленные при неизвестных и свободных членах системы уравнений задачи. План х-(х_х,х₂,...,х_п)называется опорным планом ОЗЛП,

если система векторов А/, входящих в разложение (2.5) с поло­жительными коэффициентами Xj, линейно независима. Так как векторы Aj являются m-мерными, то из определения опорного плана следует, что число его положительных компонентов может превысить га. Опорный план называется невырожденным, если он содер­жит ровно га положительных компонентов.

Если в опорном плане число положительных компонентов меньше га, то план является вырожденным.

Часто в практике рыночных условий приходится решать за­дачи оптимизации объемов выпуска продукции и расширения ее номенклатуры для сохранения достигнутого уровня прибыли в условиях насыщения рынка. Часто необходимо принимать управ­ляющие решения по выбору направлений деятельности предпри­ятий, обеспечивающие max прибыль при ограниченных ресурсах. В этих целях применяют как простые способы (например, по­строение графиков, см. пример 1), так и более сложные, исполь­зуя расчеты (см. примеры 2 и 3).

Пример 1. На предприятии выпускают два вида продукции: мотоциклы и велосипеды. Исходя из возможностей сборочного цеха, в нем могут собирать или 25 мотоциклов в день, или 100 ве­лосипедов в день, либо комбинацию тех и других, определяемую приемлемыми трудозатратами. Склад может принять не более 70 изделий любого вида в сутки. Мотоцикл стоит в 2 раза дороже ве­лосипеда. Требуется определить такой план выпуска продукции, который обеспечил бы предприятию наибольшую выручку.

Обозначим:

X— число выпускаемых мотоциклов в день.

Y— число выпускаемых велосипедов в день.

Т\ — время (в часах) производства одного мотоцикла.

Т₂ — время (в часах) производства одного велосипеда.

Из условия задачи следует, что Т\ = 4Т₂.

Если завод работает круглосуточно, то при одновременном выпуске обоих изделий

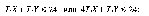
АХ + Y < 24/Т₂, но 24/Т₂ — max число производимых велосипе­дов, равное 100. Итак: 4Х+ Y < 100.

Еще одно условие — ограниченная емкость склада

Обозначим цену мотоцикла щ (руб.), цену велосипеда — а₂ (руб.). По условию: а\ = 2а₂.

Следовательно, общая цена дневной продукции S

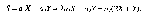
Поскольку а₂ — заданная положительная константа, то наи­большего значения следует добиваться от величины F = 2Х + Y.

Учитывая все условия задачи, приходим к ее математической модели: среди неотрицательных целочисленных решений систе­мы линейных неравенств

найти такое, которое соответствует максимуму линейной функ­ции F = 2Х + Y. (**)

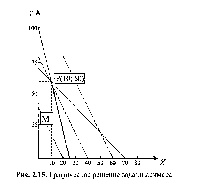
Проще всего задачу решить геометрически (см. рис. 2.15). Построим на плоскости (х, у) область, соответствующую нера­венствам (*) и условию не отрицательности х и у. Эта область М выделена жирной линией. Всякая ее точка удовлетворяет усло­вию (*) и условию неотрицательности переменных. Пунктирные линии — семейство прямых, удовлетворяющее уравнению (**) (с разными значениями константы с). Вполне очевидно, что наи­большему возможному (max) значению F, вместе с предыдущими условиями, соответствует пунктирная линия, соприкасающаяся с областью М в точке Р. Этой линии соответствует F = 80. Пунк­тирные линии правее и левее не имеют общих точек с жирной линией. Координаты точки Р(10; 60) — искомый оптимальный план производства.

Пример 2. АО «Садко» ведет ежедневный учет:

• обьемов выпускаемой продукции (кондитерских изделий — кг/сутки);

• суммарных затрат на суточный выпуск;

• выручки и суточного размера прибыли.

Эти данные по каждому цеху ежедневно представляют руко­водству в виде компьютерных распечаток.

Объемы выпуска определяются объемами поставок и стрем­лением получить максимально возможную прибыль при имею­щихся мощностях предприятия.

Вопрос: Оптимальны ли сейчас объемы выпуска?

Оптимизация может быть осуществлена на базе модели ли­нейного программирования. В качестве оптимизируемых пара­метров (управляемых переменных) Х1-Х8 выберем объемы вы­пуска продукции (в кг) из приведенных восьми переменных Xi. Для построения модели получим на основании данных номенкла­туры таблицы удельные показатели производства, рассчитанные на единицу выпуска продукции. Удельная себестоимость опреде­ляется как себестоимость/объем, а удельная прибыль как прибыль/объем.

Ц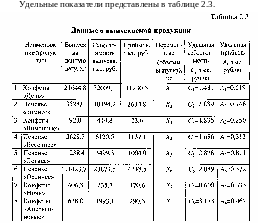 елевая функция — суммарная себестоимость, которую сле­дует минимизировать:

F (х) = С\Х_Х + C₂X₂ + с3а3 + с₄а'₄ + CjA'j + с₆а₆ + С₁Х₁ + cgag —> 1ТПП

В такой постановке можно прийти к абсурдному выводу, что для достижения абсолютного минимума себестоимости ничего не надо производить. Поэтому следует ввести разумное ограничение — требование обеспечить достижение уровня суммарной суточной прибыли N = 20 569 руб. Ограничение G\(x) запишется так:

Gj (а) = а,а, + а₂х₂ + «зА₃ + а₄х₄ + а₅х₅ + а₆х₆ + а₁х₁ + а_%х_% < N.

Математическая постановка задачи: найти управляющие пе­ременные X\-Xiy обеспечивающие минимум целевой функции при выполнении ограничения.

Решение этой задачи в Microsoft Excel с помощью инстру­мента Поиск решения в меню Сервис аналогично приведенно­му в [11].

Анализируя полученные при расчетах данные, можно опре­делить возможности сбыта.

Можно вычислить и альтернативные варианты сбыта.

Если рынок насыщен, коэффициенты возможного сбыта сни­жаются. Выход — расширение номенклатуры выпускаемой про­дукции. Строится модель с дополнительной номенклатурой.

Пример 3. Транспортная задача.

Классическая транспортная задача (задача Хитчкока-Куп-манса) — задача о поставке грузов от поставщиков к потребите­лям. Является типовой задачей для промышленных фирм, имею­щих несколько предприятий, рынков сбыта и оптовых баз. Реше­ние сводится к выбору оптимальных маршрутов, особенно когда фирмы ежемесячно пересматривают свои планы распределения продукции и номенклатура заказов меняется. Если нет других приоритетных целей, то задача состоит в том, чтобы минимизи­ровать транспортные расходы.

Например, сталь вырабатывается на т заводах Р\, Р₂, Р„. Ежемесячная выработка а_и а₂, а,„ (т/мес).Сталь надо доста­вить на предприятия Q\,Q₂, <2ь причем b_ub₂, b_k — ежеме­сячная потребность этих предприятий, с — стоимость перевозки одной тонны стали с завода Р, на предприятие Qj.

Общее производство стали равно суммарной потребности в ней (производство): а\ + а₂ + ... + а_т = b] + Ь₂ + ... + Ь_к (потребность).

Необходимо составить план перевозок, при котором:

1) удовлетворялась потребность в стали предприятий <2ь Qi,

.... «2*;

2. с заводов Р„ ...,Р_т вывозилась вся сталь;

3. общая стоимость перевозок была минимальной.

Обозначим через Ху количество стали (в тоннах), предназна­ченной к отправке с завода Р, на предприятие Qj. План перевозок состоит из (т; к) неотрицательных чисел Х_{] (i = 1, 2, m; j = 1, 2, к). Схему перевозок стали см. в табл. 2.4.

Первое условие примет вид:

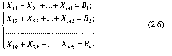
Раз стоимость перевозки одной тонны Р,- в Q, равна Су, то общая стоимость S всех перевозок равна:

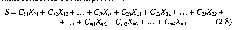
Приходим к чисто математической задаче: Дана система т + к линейных алгебраических уравнений (2.6) и (2.7) с mк неиз­вестными (обычно mк m + к)и линейная функция S (2.8). Тре­буется среди всех неотрицательных решений данной системы найти такое, при котором функция S минимизируется. Практиче­ское значение этой задачи огромно, ее умелое решение в масшта­бах страны могло бы экономить ежегодно огромные средства.

Решение транспортной задачи студентам рекомендуется вы­полнить в качестве самостоятельной работы. Пример выполнения приведен в Приложении 4.