
Графічне розв’язання задачі лінійного програмування
Мета – опанувати ідею розв’язання задачі лінійного програмування та набути навиків розв’язування їх графічним методом

Розв’яжемо задачу графічним способом. Для цього в системі координат Х10Х2 побудуємо рівняння прямих: x1+x2=3; x1-x2=3; -6x1+4x2=12; x1=1, x2=4. Відмітимо стрілками ті півплощини, які задовільняють кожній відповідній нерівності системи нерівностей стандартній формі запису задачі. Перетин півплощин - чотирикутник АBСD, який є областю допустимих розв’язків задачі. Далі будуємо вектор F(6,1) і перпендикулярно до нього пряму, яка проходить через точку (0,0). Пересуваємо цю пряму в напрямку вектора F до тих пір, поки вона не доторкнеться першої точки області допустимих значень. Це точка B.

Координати
точки B
знаходимо з рівнянь x1+x2=3
та x1=1.
Маємо x1=1
x2=2;.
В цій точці функція F
набуває свого найменшого значення
![]() 6*1+1*2+3=10.
6*1+1*2+3=10.
Симплекс-метод
Мета – навчитися знаходити початковий опорний план, здійснювати перехід до іншого опорного плану та обчислювати оптимальний план задачі лінійного програмування за критерієм оптимальності
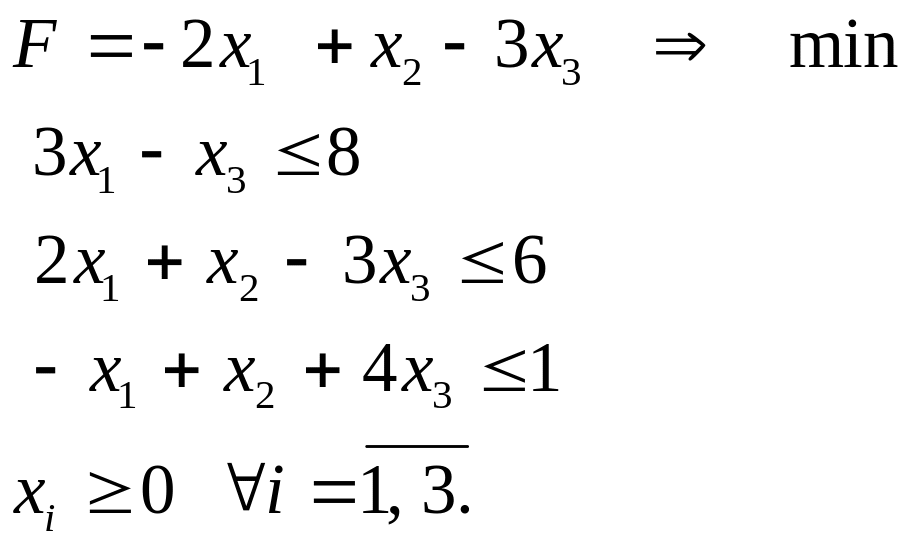
Розв’язання задачі здійснюється поетапно.
Етап
1. Знайдемо початковий опорний план.
Для цього за допомогою додаткових
змінних зведемо задачу до канонічної
форми. Оскільки цільова функція прямує
до мінімуму, то її запишемо
у вигляді:
![]() .
Обмеження: нерівності зведемо до
рівностей введенням додаткових змінних
.
Обмеження: нерівності зведемо до
рівностей введенням додаткових змінних
![]()
![]()
![]()
![]()
![]() .
Задача в канонічній формі має такий
вигляд:
.
Задача в канонічній формі має такий
вигляд:
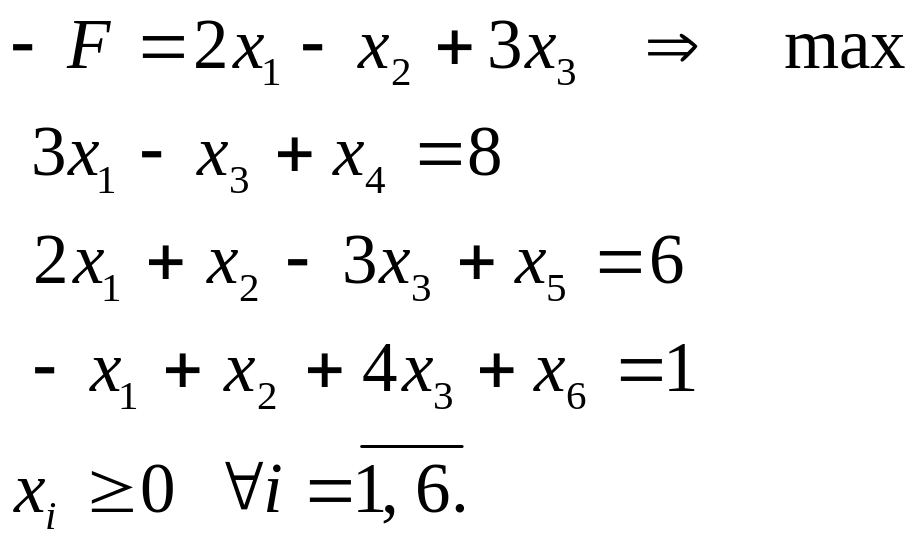
Запишемо систему обмежень у векторній формі:
![]()
де
![]() ─
─
![]() -
вимірний вектор-стовпець коефіцієнтів
при
-
вимірний вектор-стовпець коефіцієнтів
при
![]() (j=1,…,6)
(j=1,…,6)
![]() ─
-
вимірний вектор-стовпець вільних членів
системи
─
-
вимірний вектор-стовпець вільних членів
системи
 ;
;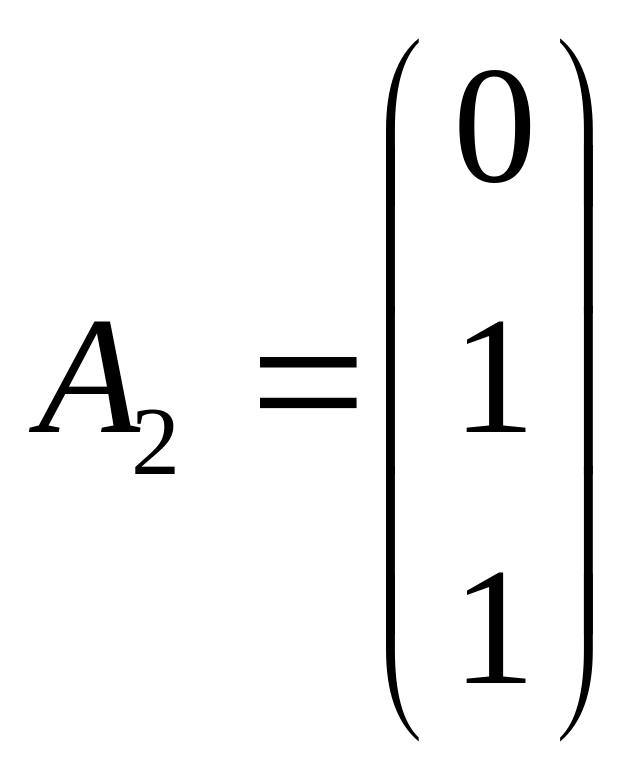 ;
;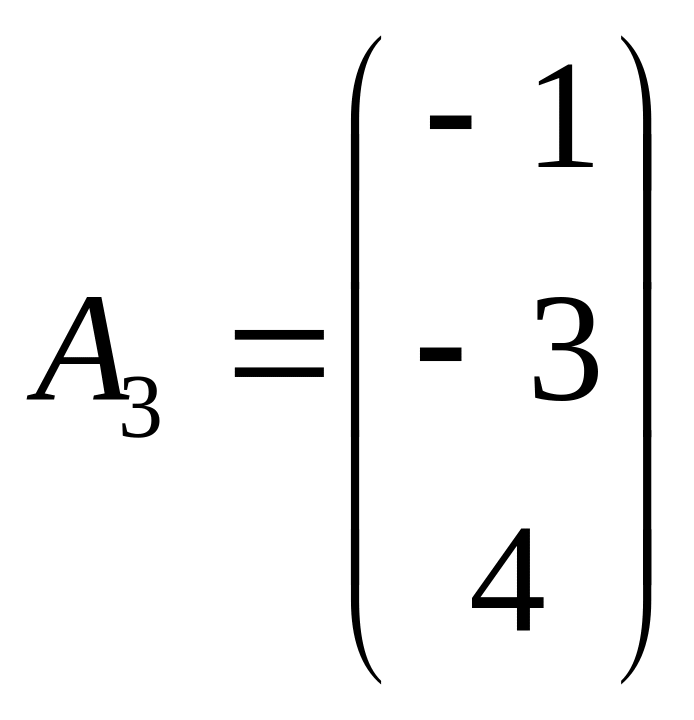 ;
; ;
;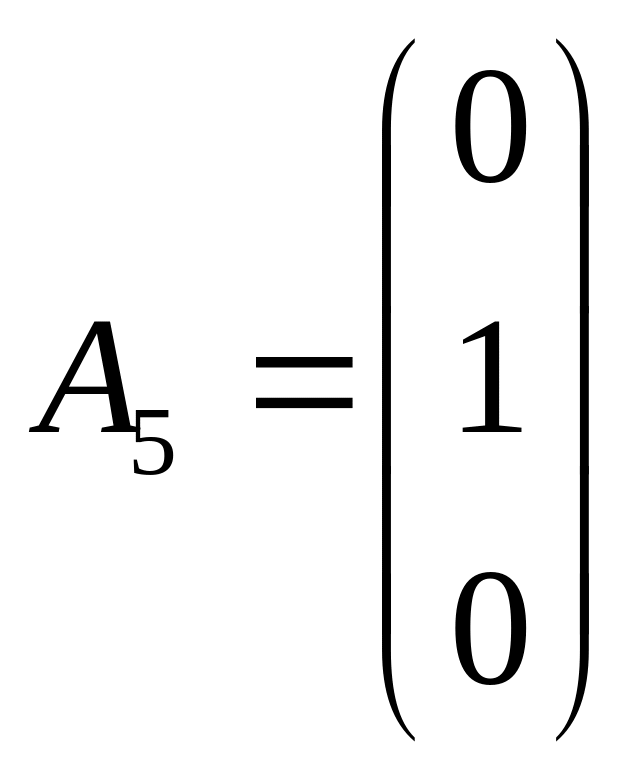 ;
;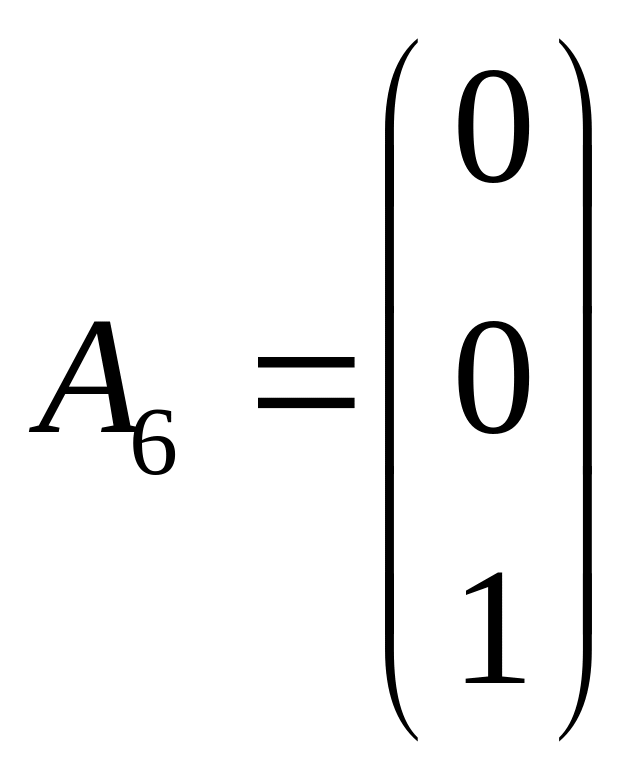 ;
; .
.
Вектори A4, A5, A6 - одиничні і лінійно-незалежні між собою вектори. Вони утворюють базис. Змінні x4, x5, x6 називаються базисними, змінні x1, x2, x3 ─ вільними і прирівнюються до нуля. У результаті отримуємо
![]()
або
![]()
Оскільки праворуч стоять всі невід’ємні коефіцієнти, а вектори A4, A5, A6 ─ лінійно-незалежні одиничні, то отримаємо початковий опорний план:
![]() .
.
Етап 2. Складаємо симплекс-таблицю (табл.1) і перевіряємо цей план на оптимальність.
Таблиця 1
і |
Базис |
Сбаз |
A0 |
C1=2 |
C2=-1 |
C3=3 |
|
|
|
A1 |
A2 |
A3 |
A4 |
A5 |
A6 |
||||
1 |
A4 |
0 |
8 |
3 |
0 |
-1 |
1 |
0 |
0 |
2 |
A5 |
0 |
6 |
2 |
1 |
-3 |
0 |
1 |
0 |
3 |
A6 |
0 |
1 |
─1 |
1 |
4 |
0 |
0 |
1 |
m+1 |
|
|
|
|
|
3=3 |
4=0 |
5=0 |
6=0 |
Перший стовпець містить номер рядка (обмеження), другий – базисні вектори. Оскільки x4, x5, x6 ─ базисні змінні, то відповідні їм вектори A4, A5, A6 ─ базисні. Третій стовпець Сбаз ─ коефіцієнти цільової функції при базисних векторах c4=0, c5=0, c6=0. Стовпець A0 ─ коефіцієнти опорного рішення. Оскільки x4, x5, x6 дорівнюють правим частинам обмежень, то ці значення записуємо у стовпець A0. В перший рядок табл.1 записуємо значення цільової функції c1=2, c2=-1, c3=3, c4=0, c5=0, c6=0
У стовпцях A1, A2, A3, A4, A5, A6 записуємо відповідні коефіцієнти в обмеженнях задачі при невідомих x1, x2, x3, x4, x5, x6.
У
(m+1) рядку
підраховуємо значення цільової функції
на даному опорному плані. Значення
![]() дорівнює скалярному добутку вектора
дорівнює скалярному добутку вектора
![]() на вектор A0:
на вектор A0:
![]()
Оцінки
![]() в (m+1) рядку
обчислюються за формулою
в (m+1) рядку
обчислюються за формулою
![]()
тобто
від скалярного добутку вектора
на вектор
![]() віднімаємо значення коефіцієнта цільової
функції
віднімаємо значення коефіцієнта цільової
функції
![]() .
Так,
.
Так,
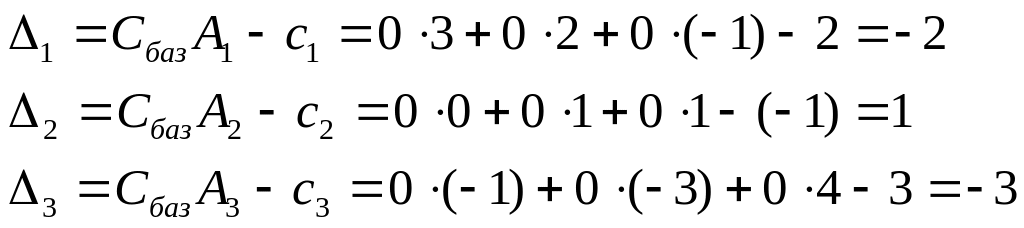
Зазначимо,
що в (m+1)
рядку базисним змінним завжди відповідають
оцінки
![]() .
Тому далі на відповідних позиціях можна
ставити нулі.
.
Тому далі на відповідних позиціях можна
ставити нулі.
Оскільки
серед оцінок
![]() є від’ємні числа, то опорний план
є від’ємні числа, то опорний план
![]() (0;
0; 0; 8; 6; 1) не є оптимальним і
необхідно перейти до наступного опорного
плану.
(0;
0; 0; 8; 6; 1) не є оптимальним і
необхідно перейти до наступного опорного
плану.
Етап
3. Для збільшення значення
цільової функції (задача, яку розв’язуємо
на максимум) серед оцінок
треба вибрати найменшу – це
![]() .
Стовпець A3
тепер називаємо розв’язуваним (напрямним)
і A3
вводимо в базис.
.
Стовпець A3
тепер називаємо розв’язуваним (напрямним)
і A3
вводимо в базис.
Далі визначаємо розв’язуваний рядок. Для цього обчислюємо відношення компонент вектора A0 до додатних компонент вектора, який вводимо в базис (A3), і серед них обираємо найменше значення
![]()
Рядок, який відповідає мінімальному відношенню, називається розв’язувальним. Вектор A6 виводимо з базису.
Елемент, що стоїть на перетині розв’язуваного рядка і розв’язуваного стовпця, називається розв’язуваним елементом.
Далі, використовуючи жорданові виключення, перераховуємо всі елементи таблиці. Знаходимо новий опорний план у новому базисі (табл. 2).
Таблиця 2
і |
Базис |
Сбаз |
A0 |
C1=2 |
C2=-1 |
C3=3 |
|
|
|
A1 |
A2 |
A3 |
A4 |
A5 |
A6 |
||||
1 |
A4 |
0 |
8,25 |
2,75 |
0,25 |
0 |
1 |
0 |
0 ,25 |
2 |
A5 |
0 |
6,75 |
1,25 |
1 |
0 |
0 |
1 |
0,75 |
3 |
A3 |
3 |
0,25 |
-0,25 |
0,25 |
1 |
0 |
0 |
0,25 |
m+1 |
|
|
0,75 |
-2,75 |
1 ,75 |
0 |
0 |
0 |
0,75 |
У табл. 2 в стовпці “Базис” замість A6 записуємо вектор A3.
У стовпці проти A3 записуємо значення коефіцієнта цільової функції с3 = 3.
У стовпцях A3, A4, A5, які відповідають базисним векторам, записуємо одиничні вектори. Підраховуємо елементи нової симплекс-таблиці.
Всі елементи розв’язуваного рядка (крім ) ділимо на розв’язуваний елемент. Інші елементи табл.2 перераховуємо за формулою жорданових виключень за правилом прямокутника.
Стовпці:
![]() ,
,
![]() ,
,
![]() ,
,
![]()
Далі обчислюємо коефіцієнти (m+1) рядка.
В
табл.2 в
![]() рядку
рядку
![]() <0,
і тому новий опорний план
<0,
і тому новий опорний план
![]() також не є оптимальним, його
можна поліпшити за рахунок введення в
базис вектора A1.
Тепер розв’язуваний стовпець - A1.
також не є оптимальним, його
можна поліпшити за рахунок введення в
базис вектора A1.
Тепер розв’язуваний стовпець - A1.
Визначимо
розв’язуваний рядок. Для цього обчислимо
![]()
Отже, 2,75 є розв’язуваним елементом, перший рядок ─ розв’язуваний, вектор A4 слід вивести з базису.
Аналогічно здійснюємо розрахунки симплекс-таблиць. Результати наведено табл. 3.
Таблиця 3
і |
Базис |
Сбаз |
A0 |
C1=2 |
C2=-1 |
C3=3 |
|
|
|
A1 |
A2 |
A3 |
A4 |
A5 |
A6 |
||||
1 |
A1 |
2 |
3 |
1 |
0,09091 |
0 |
0,36364 |
0 |
0,09091 |
2 |
A5 |
0 |
3 |
0 |
1,63636 |
0 |
-0,4545 |
1 |
0,63636 |
3 |
A3 |
3 |
1 |
0 |
0,27273 |
1 |
0,09091 |
0 |
0,27273 |
m+1 |
|
|
9 |
0 |
2 |
0 |
1 |
0 |
1 |
Оскільки
всі оцінки
![]() ,
то отриманий опорний план
,
то отриманий опорний план
![]() є оптимальним. Максимальне значення
цільової функції
є оптимальним. Максимальне значення
цільової функції
![]() .
Оскільки початкова задача була на
мінімум цільової функції, то
.
Оскільки початкова задача була на
мінімум цільової функції, то
![]()

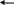
 2=1
2=1