3. Спектральный анализ непериодических сигналов. Преобразование Фурье

Рассмотренный выше гармонический анализ периодических колебаний можно распространить и на непериодические колебания. Пусть такое колебание s(t) задано в виде некоторой функции, отличной от нуля в промежутке (t₁, t₂) (рис. 2.2).

Выделив произвольный отрезок времени Т, включающий в себя промежуток (t₁, t₂), мы можем представить заданное колебание в виде ряда Фурье (2.17):

0 < t < T, (2.19)

где w₁ = 2/T, а коэффициенты C_n в соответствии с (2.18)

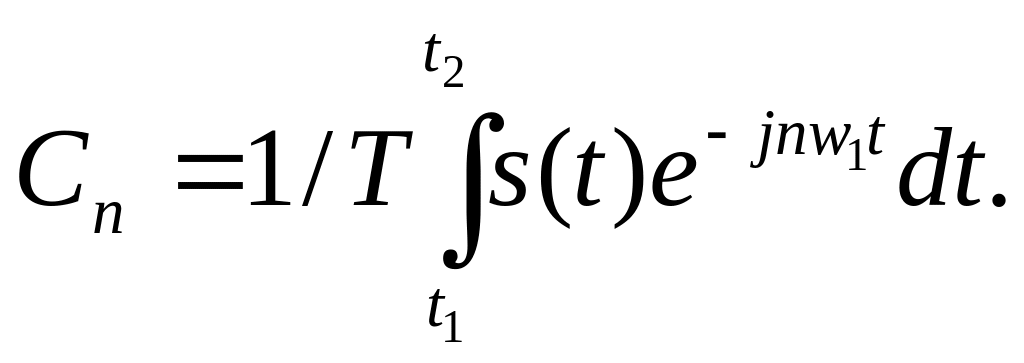(2.20)

Подставив (2.20) в (2.19), получим

0 < t < T. (2.21)

Здесь учтено, что T = 2/w₁. Вне отрезка (0, Т) ряд (2.19) определяет периодическую функцию, полученную повторением s(t) вправо и влево с периодом Т. Для того, чтобы вне отрезка (0, Т) функция равнялась нулю, величина Т должна быть бесконечно большой. Но чем больше отрезок Т, выбранный в качестве периода, тем меньше коэффициенты С_n.

Рис. 2.2 – Одиночный импульс

Устремляя Т к бесконечности, в пределе получаем бесконечно малые амплитуды гармонических составляющих (С_n→0), сумма которых изображает исходную непериодическую функцию s(t), заданную в интервале t₁ < t < t₂ (рис. 2.2). Число гармонических составляющих, входящих в ряд Фурье, будет при этом бесконечно большим, т.к. при Т   основная частота функции w₁ = 2/T  0. Иными словами, расстояние между спектральными линиями, равное основной частоте w₁, становится бесконечно малым, а спектр – сплошным.

Поэтому можно в выражении (2.21) заменить w₁ на dw, nw₁ на текущую частоту w, а операцию суммирования – операцией интегрирования. Таким образом, приходим к двойному интегралу Фурье:

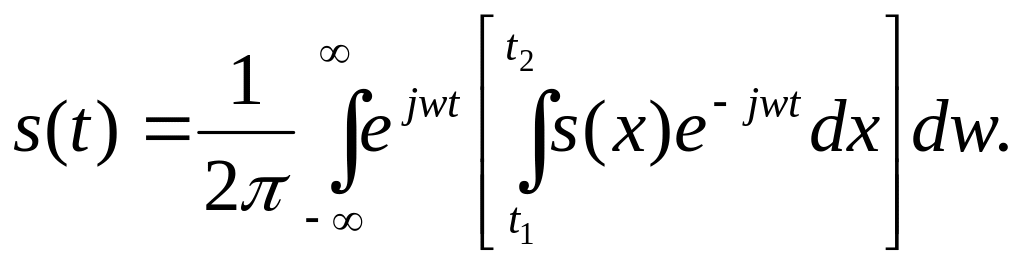(2.22)

Внутренний интеграл, являющийся функцией частоты w, является основной частотной характеристикой непериодического сигнала и называется спектральной плотностью или спектральной характеристикой функции s(t):

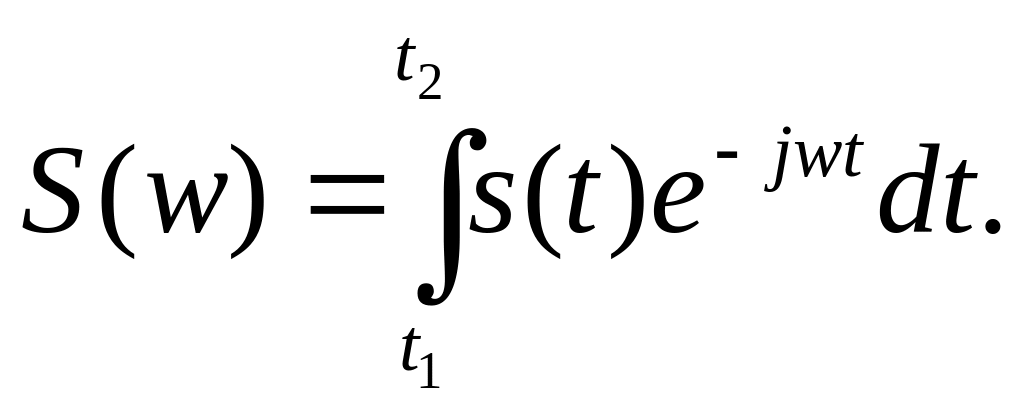(2.23)

В общем случае, когда пределы t₁ и t₂ не уточнены, спектральная плотность записывается в форме:

(2.24)

После подстановки (2.24) в выражение (2.22) получаем:

(2.25)

Выражения (2.24) и (2.25) называются соответственно прямым и обратным преобразованиями Фурье.

Таким образом, можно сделать фундаментальный вывод: сигнал s(t) и его спектральная плотность S(w) взаимно-однозначно связаны прямым и обратным преобразованиями Фурье.

Выражение (2.24) отличается от (2.18) только отсутствием множителя 1/T. Следовательно, спектральная плотность S(w) обладает всеми основными свойствами коэффициентов C_n комплексного ряда Фурье. Тогда, по аналогии, как любую комплексно-значную функцию, ее можно записать в алгебраической и экспоненциальной формах:

S(w) = A(w) - jB(w) = |S(w)| exp(j(w)), (2.26)

где

(2.27)

Модуль и аргумент спектральной плотности определяются выражениями:

(2.28)

(2.29)

Выражение (2.28) можно рассматривать как амплитудно-частотную, а (2.29) – как фазочастотную характеристику сплошного спектра непериодического колебания.

Как и в случае ряда Фурье, |S(w)| является четной, а (w) – нечетной функцией частоты w.

Используя экпоненциальную форму (2.26), можно произвести обратное преобразование Фурье (2.25) к тригонометрической форме:

Из четности модуля и нечетности фазы следует, что подынтегральная функция в первом интеграле является четной, а во втором - нечетной относительно w. Следовательно, второй интеграл равен нулю, и окончательно можно получить:

(2.30)

Из сопоставления (2.17) и (2.25) видно, что величина (1/2)S(w)dw = S(w)df имеет смысл коэффициента C_n (бесконечно малого) комплексного ряда Фурье при частоте w = 2f. Соответственно из сопоставления (2.30) и (2.15) видно, что величина (1/)S(w)dw = 2S(w)df имеет смысл амплитуды A_n (бесконечно малой) гармонической составляющей частоты w = 2f. Из этих сопоставлений становится ясным смысл термина «спектральная плотность»: 2S(w) есть амплитуда колебания, приходящаяся на 1 Гц в бесконечно узкой полосе частот, включающей в себя рассматриваемую частоту w, т.е. модуль спектральной плотности с точностью до коэффициента 1/Т (для комплексных рядов Фурье) и 2/Т (для тригонометрических) является огибающей спектра периодической последовательности подобных импульсов; соответственно аргумент спектральной плотности является огибающей фазового спектра соответствующего периодической сигнала.