1. Составная квадратурная формула трапеций:

2. Формула Гаусса:

3. Формула Симпсона:

4 . Формула левых и правых прямоугольников:

где - точки разбиения отрезка интегрирования на N частей, , .

Интеграл вычисляется с точностью . Точность вычисления интеграла определяется сравнением результатов при различном числе разбиения отрезка интегрирования. Именно, точность считается достигнутой, если

, .

Вычисление интеграла реализовано с помощью метода Calc класса IntegralHelper. Параметрами этого метода являются:

1. Объект перечисления SumAlgorithm, который устанавливает способ вычисления сумм.

2. Параметры c и d типа double, устанавливающие пределы интегрирования

3. Делегат типа Calc phi, реализующий вычисление функции phi в любой точке с заданной точностью.

4. Параметр precision типа double, задающая точность вычисления интеграла.

5. Выходной параметр типа int N, в котором возвращает кол-во вычислений, которое было выполнено для достижения точности.

Такой подход к реализации вычисления интеграла позволяет абстрагироваться как от реализации вычисления подинтегральной функции, так и от алгоритма вычисления сумм.

public class IntegralHelper {

public double Calc(SumAlgorithm sumAlgorithm, double c, double d, Calc phi, double precision, out int N) {

const double EPSILON = 0.000001;

Func<double, double> f = (x) => phi(x, EPSILON);

N = 2;

double result = 0;

AbstractSumAlgorithm sumAlgorithmMethod = SumAlgorithmFactory.GetSumAlgorithm(sumAlgorithm);

while (Math.Abs(sumAlgorithmMethod.S(c, d, f, N) - (result = sumAlgorithmMethod.S(c, d, f, 2*N))) > precision) {

N *= 2;

}

return result;

}

}

За получение реализации вычисления сумм при вычислении интеграла отвечает класс SumAlgorithmFactory. Для того чтобы получить конкретную реализацию абстрактного класса AbstractSumAlgorithm, необходимо вызвать статический метод GetSumAlgorithm с параметром типа перечисление SumAlgorithm sumAlgorithm.

public static AbstractSumAlgorithm GetSumAlgorithm(SumAlgorithm sumAlgorithm) {

return algorithms[sumAlgorithm];

}

Метод трапеции реализует класс Trapezoidal, наследуемый от абстрактного класса AbstractSumAlgorithm. Вычисление сумм реализовано в методе S этого класса. Метод S, переопределяет метод S AbstractSumAlgorithm, предоставляя конкретную реализацию этого метода.

public override double S(double c, double d, Func<double, double> f, int N) {

double result = 0;

double hN = (d - c) / N;

for (int i = 0; i < N; i++) {

double zI = c + i * hN;

double zInext = c + (i + 1) * hN;

double Si = hN * (f(zI) + f(zInext)) / 2;

result += Si;

}

return result;

}

Получим результат:

Trapezoidal method

J_o(0,00) = 1,0000; N = 2

J_o(0,30) = 0,9776; N = 4

J_o(0,60) = 0,9120; N = 4

J_o(0,90) = 0,8075; N = 4

J_o(1,20) = 0,6711; N = 4

J_o(1,50) = 0,5118; N = 4

J_o(1,80) = 0,3400; N = 4

J_o(2,10) = 0,1666; N = 8

J_o(2,40) = 0,0025; N = 8

J_o(2,70) = -0,1424; N = 8

J_o(3,00) = -0,2601; N = 8

Формула Гаусса реализуется классом Gauss, наследником класса AbstractSumAlgorithm, с методом S:

class Gauss : AbstractSumAlgorithm {

public override double S(double c, double d, Func<double, double> f, int N) {

double result = 0;

double hN = (d - c)/N;

double SQRT_3 = Math.Sqrt(3);

for(int i = 0; i < N; i++) {

double a = c + i*hN;

double b = a + hN;

double Si = (b - a)/2*(f((a + b)/2 - (b - a)/(2*SQRT_3)) + f((a + b)/2 + (b - a)/(2*SQRT_3)));

result += Si;

}

return result;

}

}

Результат:

Gauss method

J_o(0,00) = 1,0000; N = 2

J_o(0,30) = 0,9776; N = 2

J_o(0,60) = 0,9120; N = 4

J_o(0,90) = 0,8075; N = 4

J_o(1,20) = 0,6711; N = 4

J_o(1,50) = 0,5118; N = 4

J_o(1,80) = 0,3400; N = 4

J_o(2,10) = 0,1666; N = 4

J_o(2,40) = 0,0025; N = 8

J_o(2,70) = -0,1424; N = 8

J_o(3,00) = -0,2601; N = 8

Формула Симпсона:

class Simpson : AbstractSumAlgorithm {

#region Overrides of AbstractSumAlgorithm

public override double S(double c, double d, Func<double, double> f, int N) {

double result = 0;

double hN = (d - c)/N;

for(int i = 0; i< N; i++) {

double zI = c + i*hN;

double zInext = zI + hN;

double Si = (zInext - zI)/6*(f(zI) + 4*f((zI + zInext)/2) + f(zInext));

result += Si;

}

return result;

}

#endregion

}

Получим результат:

Simpson method

J_o(0,00) = 1,0000; N = 2

J_o(0,30) = 0,9776; N = 2

J_o(0,60) = 0,9120; N = 4

J_o(0,90) = 0,8075; N = 4

J_o(1,20) = 0,6711; N = 4

J_o(1,50) = 0,5118; N = 4

J_o(1,80) = 0,3400; N = 4

J_o(2,10) = 0,1666; N = 4

J_o(2,40) = 0,0025; N = 8

J_o(2,70) = -0,1424; N = 8

J_o(3,00) = -0,2601; N = 8

Формула левых прямоугольников:

class Rectangle : AbstractSumAlgorithm {

#region Overrides of AbstractSumAlgorithm

public override double S(double c, double d, Func<double, double> f, int N) {

double result = 0;

double hN = (d - c) / N;

for (int i = 0; i < N; i++) {

double a = c + i * hN;

double Si = f(a);

result += Si;

}

result = result*hN;

return result ;

}

#endregion

}

Получим результат:

Rectangle method

J_o(0,00) = 1,0000; N = 2

J_o(0,30) = 0,9776; N = 4

J_o(0,60) = 0,9120; N = 4

J_o(0,90) = 0,8075; N = 4

J_o(1,20) = 0,6711; N = 4

J_o(1,50) = 0,5118; N = 4

J_o(1,80) = 0,3400; N = 4

J_o(2,10) = 0,1666; N = 8

J_o(2,40) = 0,0025; N = 8

J_o(2,70) = -0,1424; N = 8

J_o(3,00) = -0,2601; N = 8

Результаты показали, что все формулы вычисляют интеграл правильно, с одинаковыми результатами, но метод трапеций и прямоугольников требует в среднем чуть больше итераций. Таким образом, если стоимость итерации дороже стоимости работы программиста по реализации более сложных методов Гаусса и Симпсона, то следует использовать последние.

Задание 4. Функция монотонно убывает на отрезке , следовательно, для нее существует обратная.

Для построения таблицы

			…
			…

необходимо решить уравнения итерационным методом хорд.

, , .

По итерационному методу Ньютона решение уравнения находится по формуле

, .

В нашем случае .

В качестве начального приближения к точке возьмем . Процесс останавливается, когда .

Вычисление обратной функции реализовано методом calc класса InverseFunctionHelper. Для ускорения разработки, делегаты _g (вычисляющий функцию g в произвольной точке с заданной точностью) и _g_ (вычисляющий функцию g’ в произвольной точке с заданной точностью) не были вынесены как параметры, что легко может быть исправлено с помощью современной IDE.

class InverseFunctionHelper {

public double calc (double F0, double x0, double epsilon) {

double z0 = x0;//, z1 = x0;

double z2;

Calc _g = BesselFunctionHelper.Instance.Calc;

Func<double, double> g = d => _g(d, epsilon) - F0;

Calc _g_ = BesselFunctionDerivativeHelper.Instance.Calc;

Func<double, double> g_ = d => _g_(d, epsilon);

//double gz1 = g(z1);

//double g_z1 = g_(z1);

double gz0 = g(z0);

double g_z0 = g_(z0);

if (Math.Abs(g_z0 - 0.0) < 0.000001)

return z0;

double z1 = z0 - (gz0/g_z0);

do {

double gz1 = g(z1);

double g_z1 = g_(z1);

gz0 = g(z0);

g_z0 = g_(z0);

z2 = z1 - (gz1 / g_z1) + (gz1*gz1/(gz1 - gz0))*(2/g_z1 + 1/g_z0 - 3*(z1 - z0)/(gz1 - gz0));

if(Math.Abs(z2 - z1) < epsilon) break;

z0 = z1;

z1 = z2;

} while (true);

return z2;

}

}

Получим результат:

F0 = 1, x0 = 0

F1 = 0,885449823279397, x1 = 0,686978911413385

F2 = 0,770899646558794, x2 = 0,986979585486888

F3 = 0,65634946983819, x3 = 1,22944851594628

F4 = 0,541799293117587, x4 = 1,44589535408425

F5 = 0,427249116396984, x5 = 1,64920387157837

F6 = 0,312698939676381, x6 = 1,84690480818267

F7 = 0,198148762955778, x7 = 2,04475714650771

F8 = 0,0835985862351746, x8 = 2,24845262601634

F9 = -0,0309515904854285, x9 = 2,46522792629834

F10 = -0,145501767206032, x10 = 2,70692878058248

Построим график для функции Бесселя и обратной к ней.

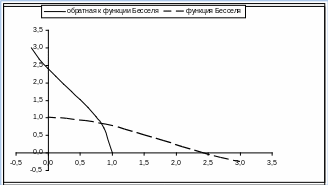
Графики функции и обратной к ней должны быть симметричны относительно оси y=x. Из рисунка видим, что обратная функция построена верно.

Производная функции g’(z) была вычислена по формуле:

И была вычислена с помощью следующего метода класса BesselFunctionDerivativeHelper:

public double Calc (double x, double epislon) {

IntegralHelper helper = new IntegralHelper();

int N;

return 1.0/Math.PI*

(helper.Calc(SumAlgorithm.Trapezoidal, 0, Math.PI,

(t, epsilon) => -Math.Cos(t)*Math.Sin(x*Math.Cos(t)), epislon, out N));

}

Листинг программы.

BesselFunctionDerivativeHelper.cs (вычисляет производную функции Бесселя)

using System;

using System.Collections.Generic;

using System.Linq;

using System.Text;

using NumericAnalysis.Integral;

namespace NumericAnalysis.FunctionHelpers {

class BesselFunctionDerivativeHelper {

private static BesselFunctionDerivativeHelper instance;

private BesselFunctionDerivativeHelper() {

}

public static BesselFunctionDerivativeHelper Instance {

get {

return instance ?? (instance = new BesselFunctionDerivativeHelper());

}

}

public double Calc (double x, double epislon) {

IntegralHelper helper = new IntegralHelper();

int N;

return 1.0/Math.PI*

(helper.Calc(SumAlgorithm.Trapezoidal, 0, Math.PI,

(t, epsilon) => -Math.Cos(t)*Math.Sin(x*Math.Cos(t)), epislon, out N));

}

}

}

BesselFunctionHelper.cs – вычисляет функцию Бесселя

using System;

using System.Collections.Generic;

using System.Linq;

using NumericAnalysis.Integral;

namespace NumericAnalysis.FunctionHelpers {

public class BesselFunctionHelper {

private static BesselFunctionHelper instance;

public static BesselFunctionHelper Instance {

get {

return instance ?? (instance = new BesselFunctionHelper());

}

}

public double[] CalcRow (double a, double b, double step, double epsilon) {

int count = Convert.ToInt32(Math.Truncate((b - a)/step)) + 1;

var result = Enumerable.Range(0, count).Select(i => a + i*step);

return CalcMany(result, epsilon);

}

public double[] CalcMany(IEnumerable<double> x, double epsilon) {

return x.AsParallel().Select(

_x => {

double S = 1;

double q = 1;

int n = 1;

while (Math.Abs(q) > epsilon) {

q = q*(-1*_x*_x/4/n/n);

S += q;

n++;

}

return S;

}).ToArray();

}

public double Calc(double x, double epsilon) {

double S = 1;

double q = 1;

int n = 1;

while (Math.Abs(q) > epsilon) {

q = q * (-1 * x * x / 4 / n / n);

S += q;

n++;

}

return S;

}

public double CalcWithIntegral(SumAlgorithm algorithm, double x, double epsilon, out int N)

{

Calc phi = (d, eps) => Math.Cos(x*Math.Cos(d));

IntegralHelper helper = new IntegralHelper();

return 1 / Math.PI * helper.Calc(algorithm, 0, Math.PI, phi, epsilon, out N);

}

}

}

Calc.cs - определяет делегат Calc

namespace NumericAnalysis.FunctionHelpers {

public delegate double Calc(double x, double epsilon);

}

AbstractSumAlgorithm.cs AbstractSumAlgorithm – абстрактный класс, наследники которого представляют реализацию вычисления суммы для алгоритма интегрирования.

using System;

namespace NumericAnalysis.Integral {

public abstract class AbstractSumAlgorithm {

public abstract double S(double c, double d, Func<double, double> f, int N);

}

}