Министерство образования и науки Российской Федерации
КАЗАНСКИЙ(ПРИВОЛЖСКИЙ) ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ
ФАКУЛЬТЕТ ВЫЧИСЛИТЕЛЬНОЙ МАТЕМАТИКИ И КИБЕРНЕТИКИ
Кафедра теоретической кибернетики
Семестровая работа по численным методам на тему:
“Табулирование трансцендентных функций”
Вариант №13.
Работу выполнил:
Студент 3-го курса
Группы 993а
Шакуров Т.Д
Работу проверила:
Гнеденкова В.Л.
Казань, 2012
Постановка задачи.
Одна из специальных функций математической физики – функция Бесселя, определяется следующим образом
Цель задания – изучить и сравнить различные способы приближенного вычисления этой функции.
Для этого:
Протабулировать
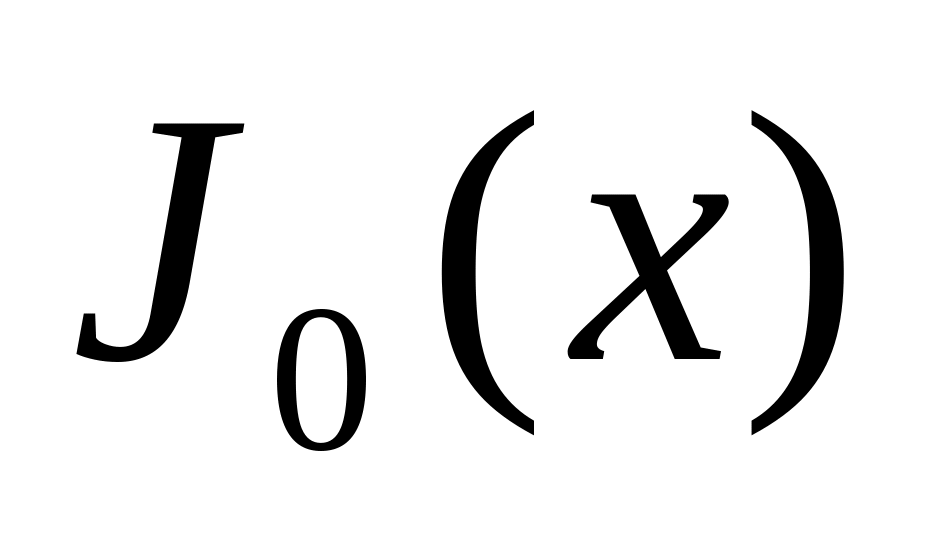на отрезке
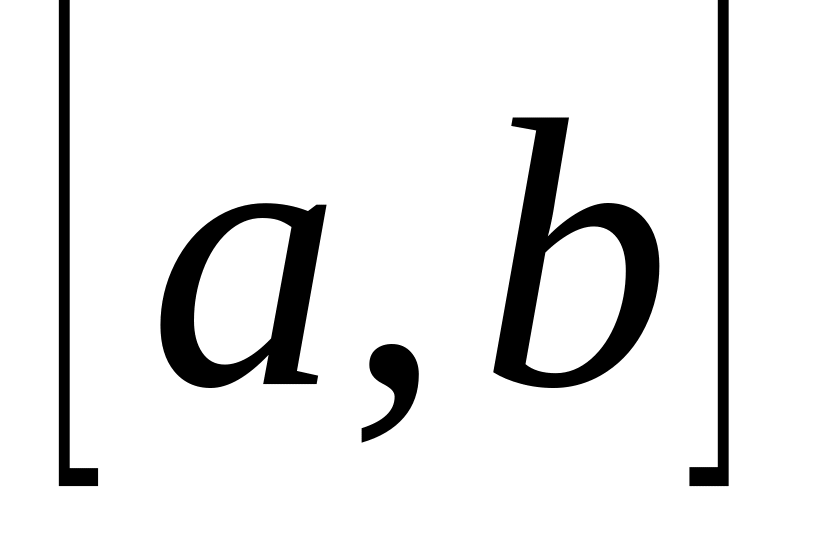с шагом h с точностью
,
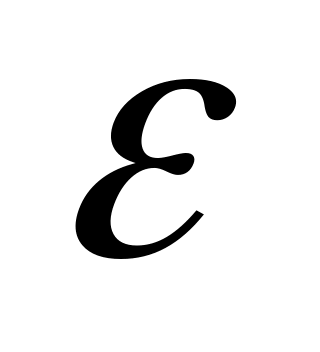основываясь на ряде Тейлора, предварительно
вычислив его
,
где
,
,
,
,
и получить, таким образом, таблицу
|
|
|
… |
|
|
|
|
… |
|
,
,
.
По приближенной таблице значений построить интерполяционный полином Ньютона, приближающий :
и вычислить погрешность интерполирования
,
.
В качестве узлов интерполяции взять:
Равномерно распределенные узлы
Корни полинома Чебышева, вычисляемые по формуле:
,
На той же сетке узлов построить таблицу приближенных значений , используя формулу
,
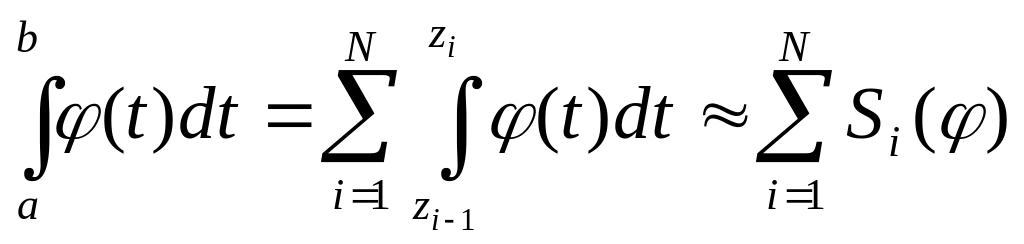где:
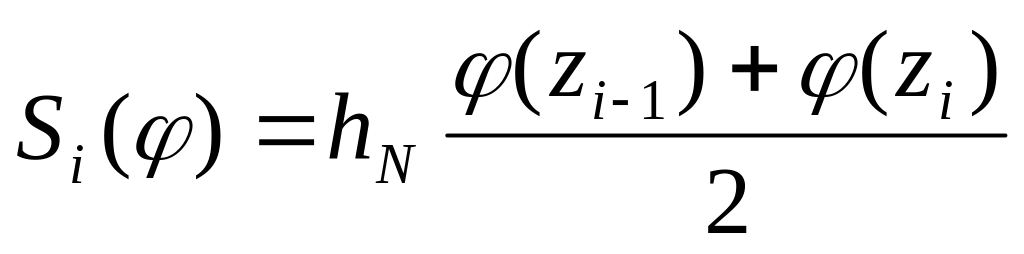(составная квадратурная формула
трапеций),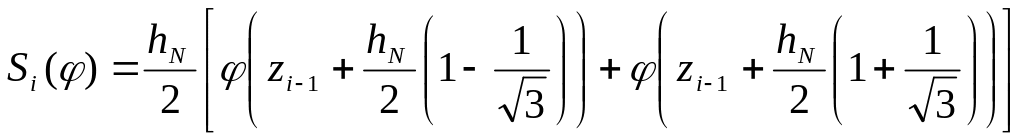
(формула Гаусса),
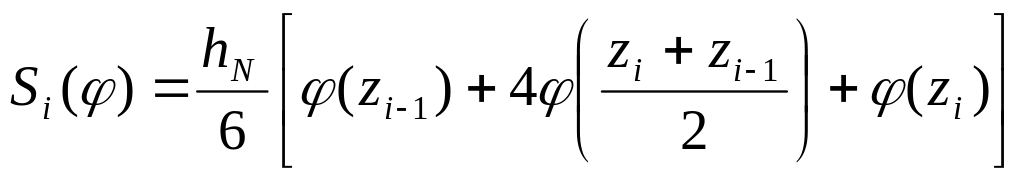(формула Симпсона),
а
- точки разбиения отрезка интегрирования
на N частей,
,
.
Интеграл вычисляется с точностью
.
Точность вычисления интеграла определяется
сравнением результатов при различном
числе разбиения отрезка интегрирования.
Именно, точность
считается достигнутой, если
,
.
Построить таблицу значений обратной к функции
|
|
|
… |
|
|
|
|
… |
|
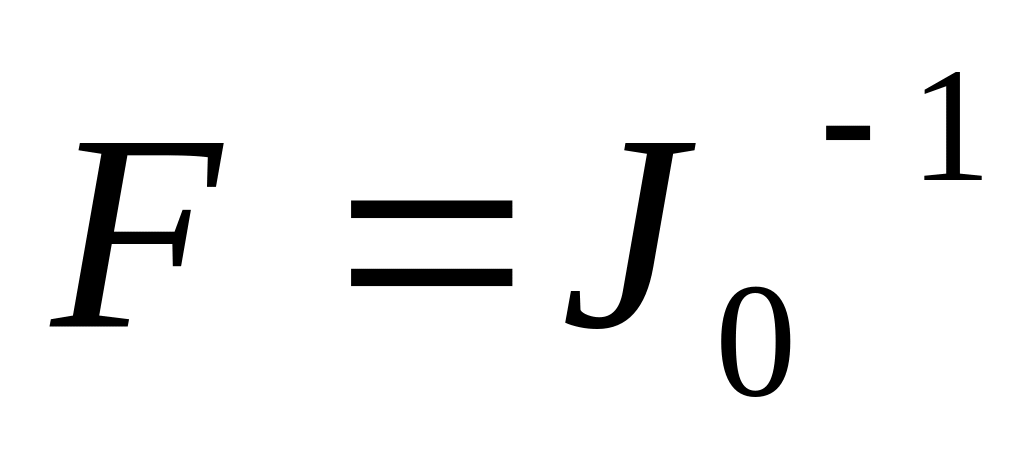
решая уравнения
,
,
,
итерационным методом Ньютона.
По итерационному методу Ньютона решение
уравнения
находится по формуле
,
.
В качестве начального приближения
к точке
взять
.
Доказательство правильности разложения в ряд функции Бесселя.
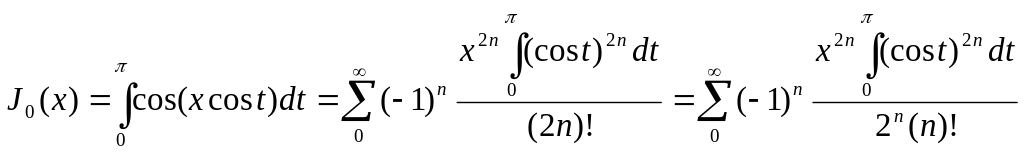
Рассмотрим
.
Воспользуемся формулой двойного угла:
.
Воспользуемся следующими равенствами
.
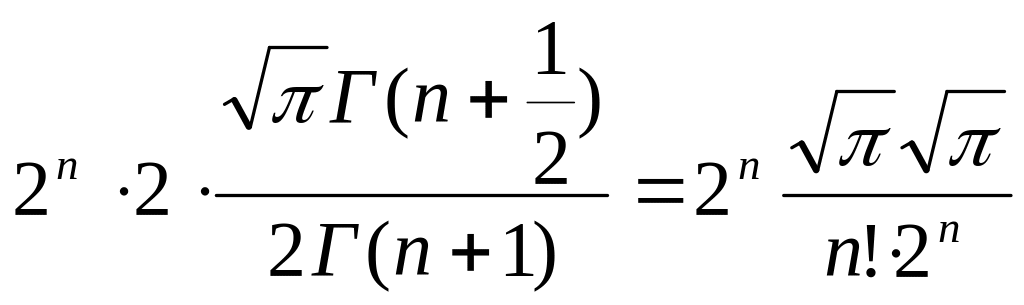
Таким образом, получаем:
Решение задачи
Задание 1.
Докажем, что степенной ряд сходится.
Для этого сначала найдем радиус сходимости
ряда :
,
где
.
Имеем:
.
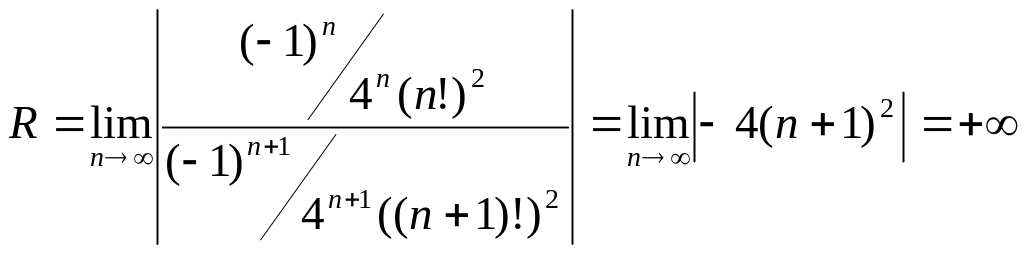Следовательно, степенной ряд сходится на всей числовой прямой. Если задать достаточно большую точность, этот ряд даст значение функции , которое будем считать точным значением.
При вычислении ряда Тейлора
будем учитывать, что каждый последующий
член ряда
получается из предыдущего
умножением на некоторую величину
,
т.е.
.
Это позволит избежать переполнения при
вычислении факториалов, встречающихся
в рассматриваемом ряде. Итак, найдём
:
.
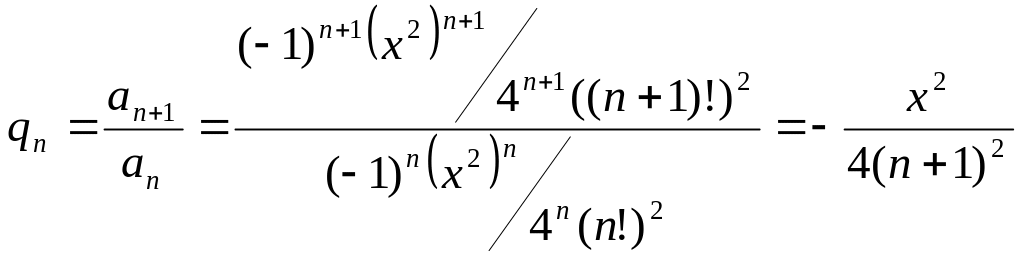Табулирование на отрезке с шагом h с точностью реализуется с помощью метода Calc класса BesselFunctionHelper, параметрами которой являются: точка х, в которой вычисляется значение функции, и точность табулирования epsilon. Также написаны вспомогательные методы CalcMany(IEnumerable<double> x, double epsilon) и CalcRow(double a, double b, double step, double epsilon), вычисляющие данный ряд для коллекции точек и для точек на заданном отрезке [a;b] с заданным интервалом step.
public double Calc(double x, double epsilon) {
double S = 1;
double q = 1;
int n = 1;
while (Math.Abs(q) > epsilon) {
q = q * (-1 * x * x / 4 / n / n);
S += q;
n++;
}
return S;
}
Протабулировав функцию , получим результаты (здесь N=10 - число разбиений):
f( 0) = 1,
f(0.3) = 0.977627,
f(0.6) = 0.912005,
f(0.9) = 0.807524,
f(1.2) = 0.671133,
f(1.5) = 0.511828,
f(1.8) = 0.339986,
f(2.1) = 0.166607,
f(2.4) = 0.00250818,
f(2.7) = -0.142449,
f( 3) = -0.260052.
Задание 2. По полученной таблице значений построим интерполяционный полином Ньютона, приближающий :
и вычислим погрешность интерполирования
, .
Разделенные разности
в формуле Ньютона будем вычислять по
следующему алгоритму.
Для
вычислим
,
.
В результате получим, что в ячейках
будут находиться соответственно
.
Вычисление интерполяционного полинома реализовано с помощью класса IntepolationPolynom. В конструкторе объекта данного класса мы передаем следующие параметры: делегат типа Calc function (делегат, с помощью которого может быть вычислено значении функции в заданной точке с заданной точностью), массива точек x и значение точности вычислений epsilon. Также существует перегрузка данного конструктора с двумя параметрами-массивами x – точек, f – значений функций в данных точках.
В конструкторе вычисляются неполные разности f(x0), f(x0, x1) и т.д.
Сами вычисления функции с помощью интерполяционного полинома выполняются при вызове метода Calc, параметром которого является arg – точка, в которой выполняются вычисления.
public InterpolationPolynom(Calc function, double[] x, double epsilon ) {
this.x = x.ToArray();
this.n = x.Length - 1;
this.f = x.Select(_x => function(_x, epsilon)).ToArray();
for (int k = 1; k <= n; k++) {
for (int i = n; i >= k; i--) {
this.f[i] = (this.f[i] - this.f[i - 1]) / (x[i] - x[i - k]);
}
}
}
public InterpolationPolynom(double[] x, double[] f) {
this.x = x;
this.n = f.Length - 1;
this.f = f.ToArray();
for(int k = 1; k<= n; k++) {
for (int i = n; i >= k; i--) {
this.f[i] = (this.f[i] - this.f[i - 1])/(x[i] - x[i - k]);
}
}
}
public double Calc(double arg) {
double S = f[n];
for (int i = n - 1; i >= 0; i--) {
S *= (arg - x[i]);
S += f[i];
}
return S;
}
Вычислим полином в 21 точке, из них 11 совпадают с точками из 1 пункта, а остальные выбираем посередине между ними. Сначала в качестве узлов интерполяции возьмем 7 равномерно распределенных узлов. Посмотрим какое значение получилось у полинома L7, у функции f и найдём максимальную погрешность из всех погрешностей для каждой точки:
Точки |
Значение f |
Значение L7 |
Значение погрешности |
0 |
1 |
1 |
0.000000000000000 |
0.15 |
0.994383 |
0.994344 |
0.000038607720850 |
0.3 |
0.977627 |
0.9776 |
0.000026863165555 |
0.45 |
0.950012 |
0.950007 |
0.000005545029786 |
0.6 |
0.912005 |
0.912012 |
0.000007388280494 |
0.75 |
0.864242 |
0.864251 |
0.000009896770748 |
0.9 |
0.807524 |
0.807528 |
0.000004299620059 |
1.05 |
0.742796 |
0.742794 |
0.000001916079670 |
1.2 |
0.671133 |
0.671128 |
0.000005456200154 |
1.35 |
0.59372 |
0.593716 |
0.000004005490506 |
1.5 |
0.511828 |
0.511828 |
0.000000000000000 |
1.65 |
0.426792 |
0.426796 |
0.000004130476664 |
1.8 |
0.339986 |
0.339991 |
0.000005585545977 |
1.95 |
0.252799 |
0.252801 |
0.000001868675833 |
2.1 |
0.166607 |
0.166603 |
0.000004272551981 |
2.25 |
0.0827501 |
0.0827408 |
0.000009236122655 |
2.4 |
0.00250818 |
0.00250086 |
0.000007319661188 |
2.55 |
-0.0729229 |
-0.0729162 |
0.000006711023728 |
2.7 |
-0.142449 |
-0.142421 |
0.000028772563696 |
2.85 |
-0.205103 |
-0.205061 |
0.000041369972738 |
3 |
-0.260052 |
-0.260052 |
0.000000000000000 |
Максимальная погрешность в этом случае равна 0.000041369972738.
Теперь в качестве узлов интерполяции возьмем корни полинома Чебышева, вычисляемые по формуле: , . (n=6). Также найдём значение функции в каждой точке и значение полинома LChebishev, вычислим максимальную погрешность в этом случае:
Точки |
Значение f |
Значение LChebishev |
Значение погрешности |
0 |
1 |
1.00001 |
0.000013368570534 |
0.15 |
0.994383 |
0.99437 |
0.000013355232776 |
0.3 |
0.977627 |
0.977624 |
0.000002636649041 |
0.45 |
0.950012 |
0.950023 |
0.000010981229075 |
0.6 |
0.912005 |
0.912019 |
0.000014116043459 |
0.75 |
0.864242 |
0.864249 |
0.000007835188342 |
0.9 |
0.807524 |
0.80752 |
0.000003708409176 |
1.05 |
0.742796 |
0.742783 |
0.000012268409319 |
1.2 |
0.671133 |
0.671118 |
0.000014662673222 |
1.35 |
0.59372 |
0.59371 |
0.000009351791575 |
1.5 |
0.511828 |
0.511828 |
0.000000000000000 |
1.65 |
0.426792 |
0.426801 |
0.000009498005332 |
1.8 |
0.339986 |
0.340001 |
0.000014859966241 |
1.95 |
0.252799 |
0.252812 |
0.000012314396924 |
2.1 |
0.166607 |
0.166611 |
0.000003768832890 |
2.25 |
0.0827501 |
0.0827427 |
0.000007347731200 |
2.4 |
0.00250818 |
0.00249357 |
0.000014602673403 |
2.55 |
-0.0729229 |
-0.0729338 |
0.000010887925142 |
2.7 |
-0.142449 |
-0.142446 |
0.000002975138280 |
2.85 |
-0.205103 |
-0.205088 |
0.000014390247566 |
3 |
-0.260052 |
-0.260067 |
0.000014357677855 |
В этом случае максимальная погрешность равна 0.000014859966241.
Построим график функции погрешности для 7 равномерно распределенных узлов и узлов-корней полинома Чебышева.
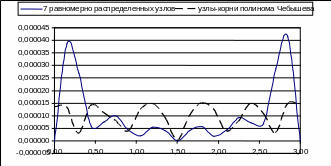
Продолжим наш эксперимент. Возьмем в качестве узлов интерполяции 11 равномерно распределенных узлов из 1 пункта. Получим результат:
Точки |
Значение f |
Значение полинома L11 |
Значение погрешности |
0 |
1 |
1 |
0.000000000000000 |
0.15 |
0.994383 |
0.994383 |
0.000000114585087 |
0.3 |
0.977627 |
0.977627 |
0.000000000000000 |
0.45 |
0.950012 |
0.950012 |
0.000000154968287 |
0.6 |
0.912005 |
0.912005 |
0.000000000000000 |
0.75 |
0.864242 |
0.864242 |
0.000000507748106 |
0.9 |
0.807524 |
0.807524 |
0.000000000000000 |
1.05 |
0.742796 |
0.742796 |
0.000000181492593 |
1.2 |
0.671133 |
0.671133 |
0.000000000000000 |
1.35 |
0.59372 |
0.59372 |
0.000000296736485 |
1.5 |
0.511828 |
0.511828 |
0.000000000000000 |
1.65 |
0.426792 |
0.426791 |
0.000000217340586 |
1.8 |
0.339986 |
0.339986 |
0.000000000000000 |
1.95 |
0.252799 |
0.252799 |
0.000000369326328 |
2.1 |
0.166607 |
0.166607 |
0.000000000000000 |
2.25 |
0.0827501 |
0.0827503 |
0.000000246297335 |
2.4 |
0.00250818 |
0.00250818 |
0.000000000000000 |
2.55 |
-0.0729229 |
-0.0729227 |
0.000000225955700 |
2.7 |
-0.142449 |
-0.142449 |
0.000000000000000 |
2.85 |
-0.205103 |
-0.205102 |
0.000000263403836 |
3 |
-0.260052 |
-0.260052 |
0.000000000000000 |
Максимальная погрешность в этом случае равна 0.000000507748106.
По таблице видим, что значения полинома в точках, совпадающих с узлами интерполяции, полностью совпадают со значениями функции в этих точках (следует из формы интерполяционного полинома).
Теперь возьмем в качестве узлов корни полинома Чебышева(n=10). Получим:
Точки |
Значение f |
Значение LChebishev |
Значение погрешности |
0 |
1 |
1 |
0.000000064264086 |
0.15 |
0.994383 |
0.994383 |
0.000000018500387 |
0.3 |
0.977627 |
0.977626 |
0.000000235344085 |
0.45 |
0.950012 |
0.950012 |
0.000000136099128 |
0.6 |
0.912005 |
0.912005 |
0.000000224820947 |
0.75 |
0.864242 |
0.864242 |
0.000000377209036 |
0.9 |
0.807524 |
0.807524 |
0.000000110464428 |
1.05 |
0.742796 |
0.742796 |
0.000000007863648 |
1.2 |
0.671133 |
0.671133 |
0.000000234496309 |
1.35 |
0.59372 |
0.59372 |
0.000000108306490 |
1.5 |
0.511828 |
0.511828 |
0.000000000000000 |
1.65 |
0.426792 |
0.426792 |
0.000000038936686 |
1.8 |
0.339986 |
0.339986 |
0.000000431431582 |
1.95 |
0.252799 |
0.252799 |
0.000000029277853 |
2.1 |
0.166607 |
0.166607 |
0.000000155689101 |
2.25 |
0.0827501 |
0.0827502 |
0.000000105575277 |
2.4 |
0.00250818 |
0.00250791 |
0.000000268504841 |
2.55 |
-0.0729229 |
-0.0729228 |
0.000000075834241 |
2.7 |
-0.142449 |
-0.142449 |
0.000000032690740 |
2.85 |
-0.205103 |
-0.205103 |
0.000000006395501 |
3 |
-0.260052 |
-0.260052 |
0.000000015211450 |
Максимальная погрешность равна 0.000000431431582.
Построим графики функций погрешности:
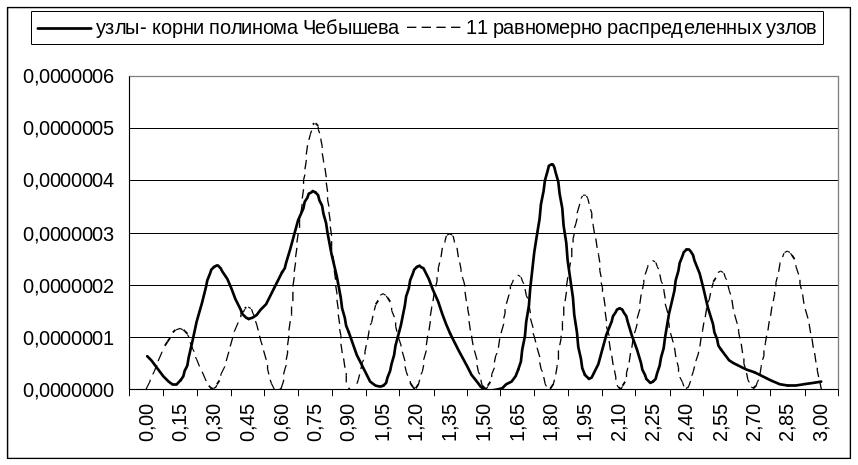
Продолжим наши вычисления. Возьмем 21 равномерно распределенный узел, будем вычислять полином в 31 точке:
Точки |
Значение f |
Значение 21 |
Значение погрешности |
0 |
1 |
1 |
0.000000000000000 |
0.1 |
0.997502 |
0.997349 |
0.000152141292050 |
0.2 |
0.990025 |
0.990058 |
0.000032576355448 |
0.3 |
0.977627 |
0.977627 |
0.000000000000000 |
0.4 |
0.960398 |
0.960395 |
0.000003217952381 |
0.5 |
0.93847 |
0.938471 |
0.000001438000290 |
0.6 |
0.912005 |
0.912005 |
0.000000000000000 |
0.7 |
0.8812 |
0.8812 |
0.000000611467709 |
0.8 |
0.846287 |
0.846287 |
0.000000278639559 |
0.9 |
0.807524 |
0.807524 |
0.000000000000000 |
1 |
0.765198 |
0.765198 |
0.000000062264589 |
1.1 |
0.719622 |
0.719622 |
0.000000093846096 |
1.2 |
0.671133 |
0.671133 |
0.000000000000000 |
1.3 |
0.620087 |
0.620086 |
0.000000777242734 |
1.4 |
0.566855 |
0.566855 |
0.000000082477166 |
1.5 |
0.511828 |
0.511828 |
0.000000000000000 |
1.6 |
0.455402 |
0.455402 |
0.000000068399129 |
1.7 |
0.397985 |
0.397984 |
0.000000092767892 |
1.8 |
0.339986 |
0.339986 |
0.000000000000000 |
1.9 |
0.281819 |
0.281818 |
0.000000225143425 |
2 |
0.223891 |
0.223891 |
0.000000135021459 |
2.1 |
0.166607 |
0.166607 |
0.000000000000000 |
2.2 |
0.110362 |
0.110362 |
0.000000145779173 |
2.3 |
0.0555401 |
0.0555403 |
0.000000210631834 |
2.4 |
0.00250818 |
0.00250818 |
0.000000000000000 |
2.5 |
-0.0483829 |
-0.048384 |
0.000001144908314 |
2.6 |
-0.096805 |
-0.096804 |
0.000000946650086 |
2.7 |
-0.142449 |
-0.142449 |
0.000000000000001 |
2.8 |
-0.185036 |
-0.185046 |
0.000010173250968 |
2.9 |
-0.224312 |
-0.224265 |
0.000046379921866 |
3 |
-0.260052 |
-0.260052 |
0.000000000000008 |
Максимальная погрешность в данном случае равна 0.000152141292050.
Вычислим полином в этих же точках, но в качестве узлов возьмем корни полинома Чебышева(n=20)
Точки |
Значение f |
Значение LChebishev |
Значение погрешности |
0 |
1 |
1 |
0.000000043204802 |
0.1 |
0.997502 |
0.997502 |
0.000000006293351 |
0.2 |
0.990025 |
0.990025 |
0.000000002758722 |
0.3 |
0.977627 |
0.977627 |
0.000000162342174 |
0.4 |
0.960398 |
0.960399 |
0.000000397374500 |
0.5 |
0.93847 |
0.93847 |
0.000000088249031 |
0.6 |
0.912005 |
0.912005 |
0.000000195578879 |
0.7 |
0.8812 |
0.881201 |
0.000000264407297 |
0.8 |
0.846287 |
0.846287 |
0.000000014084707 |
0.9 |
0.807524 |
0.807524 |
0.000000047013335 |
1 |
0.765198 |
0.765198 |
0.000000078441453 |
1.1 |
0.719622 |
0.719622 |
0.000000090446146 |
1.2 |
0.671133 |
0.671133 |
0.000000227288893 |
1.3 |
0.620087 |
0.620087 |
0.000000165515319 |
1.4 |
0.566855 |
0.566856 |
0.000000476555033 |
1.5 |
0.511828 |
0.511828 |
0.000000000000000 |
1.6 |
0.455402 |
0.455402 |
0.000000259749068 |
1.7 |
0.397985 |
0.397984 |
0.000000094153803 |
1.8 |
0.339986 |
0.339986 |
0.000000395167587 |
1.9 |
0.281819 |
0.281819 |
0.000000007781002 |
2 |
0.223891 |
0.223891 |
0.000000020731408 |
2.1 |
0.166607 |
0.166607 |
0.000000036176590 |
2.2 |
0.110362 |
0.110362 |
0.000000053661080 |
2.3 |
0.0555401 |
0.0555401 |
0.000000084467918 |
2.4 |
0.00250818 |
0.00250796 |
0.000000215547406 |
2.5 |
-0.0483829 |
-0.0483838 |
0.000000853431217 |
2.6 |
-0.096805 |
-0.0968051 |
0.000000060793142 |
2.7 |
-0.142449 |
-0.142449 |
0.000000023152738 |
2.8 |
-0.185036 |
-0.185036 |
0.000000000762105 |
2.9 |
-0.224312 |
-0.224312 |
0.000000003024774 |
3 |
-0.260052 |
-0.260052 |
0.000000016623809 |
В данном случае максимальная погрешность равна 0.000000853431217.
В сравнении с равномерно распределёнными узлами погрешность меньше на 3 порядка. Построим графики функций погрешности:
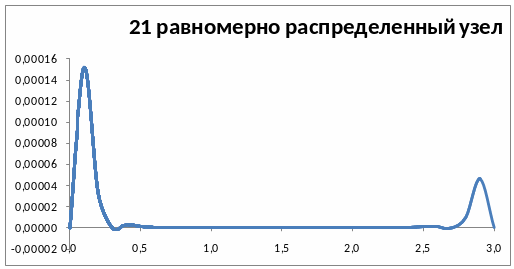
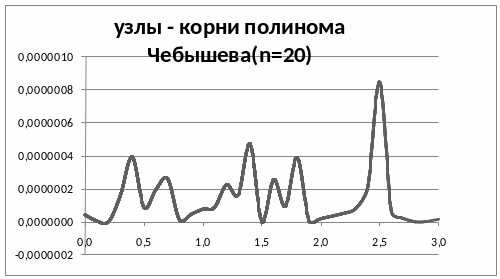
Для 31 равномерно распределенного узла получим :
Точка |
Значение f |
Значение L31 |
Значение погрешности |
0 |
1 |
1 |
0.000000000000000 |
0.15 |
0.994383 |
0.994344 |
0.000038607720850 |
0.3 |
0.977627 |
0.977627 |
0.000000000000000 |
0.45 |
0.950012 |
0.950067 |
0.000055135548585 |
0.6 |
0.912005 |
0.912005 |
0.000000000000000 |
0.75 |
0.864242 |
0.864241 |
0.000000982024340 |
0.9 |
0.807524 |
0.807524 |
0.000000000000000 |
1.05 |
0.742796 |
0.742796 |
0.000000254259569 |
1.2 |
0.671133 |
0.671133 |
0.000000000000000 |
1.35 |
0.59372 |
0.59372 |
0.000000468792162 |
1.5 |
0.511828 |
0.511828 |
0.000000000000000 |
1.65 |
0.426792 |
0.426792 |
0.000000029159881 |
1.8 |
0.339986 |
0.339986 |
0.000000000000000 |
1.95 |
0.252799 |
0.2528 |
0.000000273900596 |
2.1 |
0.166607 |
0.166607 |
0.000000000000005 |
2.25 |
0.0827501 |
0.0827487 |
0.000001400475138 |
2.4 |
0.00250818 |
0.00250818 |
0.000000000000185 |
2.55 |
-0.0729229 |
-0.0728698 |
0.000053076782670 |
2.7 |
-0.142449 |
-0.142449 |
0.000000000009240 |
2.85 |
-0.205103 |
-0.205061 |
0.000041369972738 |
3 |
-0.260052 |
-0.260052 |
0.000000000189931 |
Максимальная погрешность равна 0.000055135548585.
Теперь вычислим полином в этих же точках, но в качестве узлов возьмем корни полинома Чебышева (при n=30):
Точки |
Значение f |
Значение LChebishev |
Значение погрешности |
0 |
1 |
1 |
0.000001160841701 |
0.15 |
0.994383 |
0.994383 |
0.000000002191763 |
0.3 |
0.977627 |
0.977627 |
0.000000069739864 |
0.45 |
0.950012 |
0.950012 |
0.000000147828596 |
0.6 |
0.912005 |
0.912005 |
0.000000159221544 |
0.75 |
0.864242 |
0.864241 |
0.000000191782127 |
0.9 |
0.807524 |
0.807524 |
0.000000042120485 |
1.05 |
0.742796 |
0.742796 |
0.000000001195556 |
1.2 |
0.671133 |
0.671133 |
0.000000004013546 |
1.35 |
0.59372 |
0.59372 |
0.000000007613639 |
1.5 |
0.511828 |
0.511828 |
0.000000000000000 |
1.65 |
0.426792 |
0.426792 |
0.000000006243724 |
1.8 |
0.339986 |
0.339986 |
0.000000012160645 |
1.95 |
0.252799 |
0.252799 |
0.000000001636670 |
2.1 |
0.166607 |
0.166607 |
0.000000001127016 |
2.25 |
0.0827501 |
0.08275 |
0.000000024584625 |
2.4 |
0.00250818 |
0.00250829 |
0.000000111529981 |
2.55 |
-0.0729229 |
-0.0729226 |
0.000000299614240 |
2.7 |
-0.142449 |
-0.142449 |
0.000000044231380 |
2.85 |
-0.205103 |
-0.205103 |
0.000000008436138 |
3 |
-0.260052 |
-0.260052 |
0.000000036960039 |
Максимальная погрешность равна 0.000001160841701. Это на порядок меньше, чем при 31 равномерно распределенных узлах.
Построим график функций погрешности:
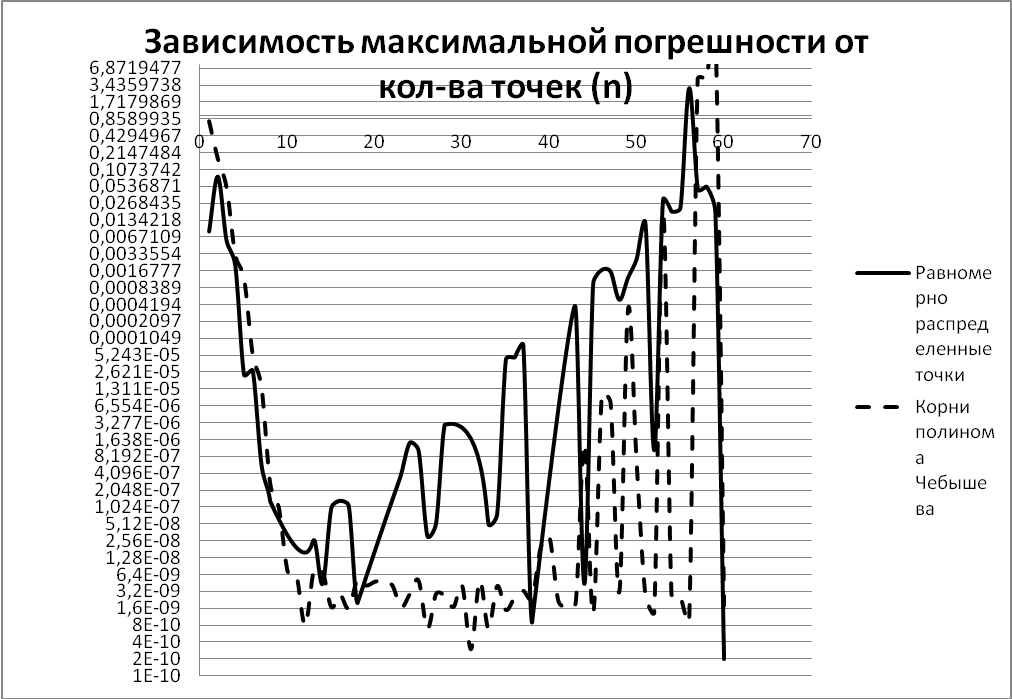
Вывод: Из проделанных экспериментов и полученных результатов мы видим, что, если в качестве узлов интерполяции брать корни полинома Чебышева, то получаем, что погрешность вычисления полинома намного меньше, чем при равномерно распределенных узлах. Из теории узнаём, что действительно, такой выбор узлов должен обеспечить максимально точное вычисление полинома. Также полученные результаты показали, что с увеличением числа узлов интерполяции увеличивается точность вычисления полинома. При этом погрешность вблизи концов рассматриваемого отрезка резко увеличивается, а в середине отрезка погрешность меньше на 1-3 порядка.
Задание 3. Вычислим интеграл
тремя разными способами и сравним
скорость вычислений каждого из них.
Интеграл вычисляется по формуле: , где: