Динамическое программирование. Основное рекуррентное соотношение Беллмана. Общие принципы решения задач динамического программирования
(аддитивность критерия, этапирование процесса)
Динамическое программирование – система методов нахождения оптимального решения задач, в которых процесс принятия решения может быть разбит на шаги. В качестве шагов могут выступать временные этапы решения (дни, месяцы, годы и т.п.) или его структурные элементы (подразделения организации, направления вложения финансовых средств и др.).
З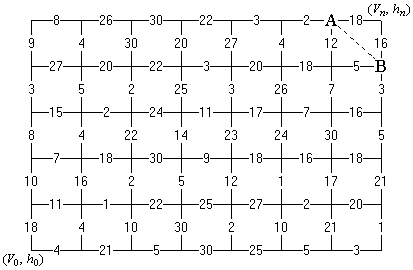
адача
о наборе скорости и высоты летательным
аппаратом.
Пусть летательный
аппарат движется со скоростью
на высоте
и должен
разогнаться
до скорости
и подняться на
высоту
.
ЭТАПИРОВАНИЕ.
Решение. Разобьём процесс набора скорости и высоты на отдельные шаги и будем считать, что за один шаг летательный аппарат набирает либо скорость, либо высоту. Нетрудно заметить, что общее число шагов представляет собой сумму числа возможных переходов по «решетке» по горизонтали (n=7) и по вертикали (m=5). Таким образом, процесс состоит из m+n=7+5 = 12 шагов.
Принцип БЕЛЛМАНА
Согласно принципу Беллмана
на каждом шаге необходимо выбирать такое условно-оптимальное управление, которое обеспечивает вместе с последующими оптимальными управлениями наилучшую траекторию, начиная с текущего шага и до конца.
Будем оптимизировать каждый шаг, начиная с последнего. (обратный ход).
АДДИТИВНОСТЬ КРИТЕРИЯ
Для простоты будем считать, что летательный аппарат на каждом шаге может либо только увеличивать скорость (перемещение вправо по «решетке»), либо только – высоту (перемещение вверх). В ДП, вообще говоря, имеют дело лишь с аддитивным критерием – когда суммарный показатель эффективности на всех шагах равен сумме эффективностей на каждом шагу.
Специальные задачи математического программирования. Задача о назначениях. Задача о коммивояжере
Комбинаторные методы оптимизации.
1°. Задача о назначениях
Пусть есть 5 человек: M1,М2,…,M5, спо-собных выполнить 5 заданий:T1,Т2,…,Т5. В силу разной подготовки и иных при-чин эффективность функционирования каждого на каждой из должностей различ-на и может быть определена (хотя бы в долях единицы). Существует n! вариантов.
Как следует распределить людей по ра-ботам, чтобы суммарная эффективность функционирования системы была наи-большей?
Для решения задачи методом Мака составляется матрица: пусть по горизонтали указаны номера работников организации, по вертикали - номера заданий, соответствующих разным должностям. Таблицу заполним значениями времени выполнения заданий. Будем искать минимальное суммарное время выполнения всех n=5 заданий.
Для примера возьмем конкретную матрицу 5 ´ 5.
|
T1 |
T2 |
T3 |
T4 |
T5 |
M1 |
10 |
5 |
9 |
18 |
11 |
M2 |
13 |
19 |
6 |
12 |
14 |
M3 |
3 |
2 |
4 |
4 |
5 |
M4 |
18 |
9 |
12 |
17 |
15 |
M5 |
11 |
6 |
14 |
19 |
10 |
В ответе будут единицы и нули, т.е. назначение\неназначение конкретного работника на конкретную работу. Важным условием является то, что один человек может быть назначен на одну работу и наоборот.
Задача о коммивояжере. Имеется n городов, которые должен обойти коммивояжер с минимальными затратами. При этом на его маршрут накладывается два ограничения:
маршрут должен быть замкнутым, т.е. коммивояжёр должен вернуться в тот город, из которого он начал движение;
в каждом из городов коммивояжер должен побывать точно один раз, т.е. нужно обязательно обойти все города, при этом не побывав ни в одном городе дважды.
Для расчета затрат существует матрица условий, содержащая затраты на переход из города в город, при этом считается, что можно перейти из любого города в любой, кроме того же самого (в матрице как бы вычеркивается диагональ). Целью решения является нахождение маршрута, удовлетворяющего всем условиям и при этом имеющего минимальную сумму затрат.
В каком порядке бродячий торговец должен объезжать n городов, чтобы минимизировать общее расстояние (стоимость) объезда, когда заданы попарно расстояния (стоимости) между всеми городами и требуется, чтобы в каждом городе он побывал ровно один раз?
Если не требовать возвращения к исходному пункту, то задача незамкнута. Мы будем говорить о замкнутой задаче.
Существует (n-1)! вариантов маршрутов.
Примеры ситуаций, где просматривается возможное использование этой задачи: сбор по тревоге, энергоснабжение, телефонная связь, определение оптимальной последовательности обработки деталей, сложные задачи теории расписаний, балансирование сборочных линий.
Введем переменные:
Целевая функция и ограничения примут вид:
Решается с помощью метода ветвей и границ. (ветвление маршрута и приведение матрицы)