Основные принципы и правила составления математических моделей
При составлении математической модели - определяется цель исследования, основные ограничения, осуществляется количественное выражение всех данных задачи.
Цель характеризуется признаком (критерием), по которому сравниваются различные варианты решения (наибольшая прибыль, наименьшие издержки, максимальное использование оборудования, достижение определенного результата в минимальное время, наименьшие отходы производства). Единого критерия быть не может, как не может быть универсального показателя экономического объекта. В каждой задаче выбирается тот из показателей, который в данном случае представляется наиболее важным.
Ограничения. Постановка задачи ЛП характерна наличием ограниченных ресурсов, которыми и следует распорядиться наилучшим образом. Самое главное – определить какие ресурсы являются лимитирующими, сдерживающими.
Ресурсы – это запасы сырья, электроэнергии, топлива, трудовые ресурсы, ресурсы оборудования, посевная площадь и т.д.
Кроме того, в систему ограничений могут входить такие характеристики или дополнительные условия, как условия комплектности, обязательности ассортимента, плановые задания по выпуску.
Все ограничения должны быть непротиворечивыми, то есть обеспечивающими существование хотя бы одного решения.
Неучет какого-либо ограничения может привести к неосуществимости полученного оптимального решения.
С другой стороны чрезвычайно жесткие ограничения могут сузить область возможных решений и не дадут выявить оптимальное.
Количественное выражение данных означает, что необходимо «заменять» оценки типа «лучше-хуже» числовыми уравнениями и неравенствами с установлением шкалы сопоставления. Например, три «двойки» не эквивалентны двум «тройкам». Выраженные количественно данные задачи записываются в форме равенств или неравенств; аналогична формализация целевой функции, где все переменные находятся в линейном соотношении и всё это составляет математическую модель.
Пример:
Цех выпускает трансформаторы двух видов. На изготовление трансформатора первого вида расходует 5 кг трансформаторного железа и 3 кг проволоки, второго вида – 3 и 2 кг. От реализации трансформаторов первого вида цех получает прибыль – 1,2 у.е. за штуку, а второго – 1 у.е. за штуку. Сколько трансформаторов каждого вида должен выпустить цех, чтобы получить наибольшую прибыль, если располагает 480 кг железа и 300 кг проволоки
Мат. модель:
|
Железо |
Проволока |
Прибыль |
I |
5 |
3 |
1,2 |
II |
3 |
2 |
1 |
|
480 |
300 |
|
5x1+ 3x2 £ 480 - ограничение по железу
3x1+ 2x2 £ 300 - ограничение по проволоке
x1, х2 ³ 0
max ( 1,2× x1+ 1× x2 ) - цель
Транспортная задача. Граф перевозок. Признак оптимальности. Метод потенциалов.
Постановка транспортной задачи. Пусть имеется несколько поставщиков однородной продукции (каждый с определенным запасом) и несколько её потребителей (с известными потребностями у каждого). Задана также сеть коммуникаций (дорог, рек, воздушных линий и т.д.), связывающая каждого поставщика с каждым потребителем. На каждой коммуникации задана цена перевозки – стоимость перевозки единицы продукции.
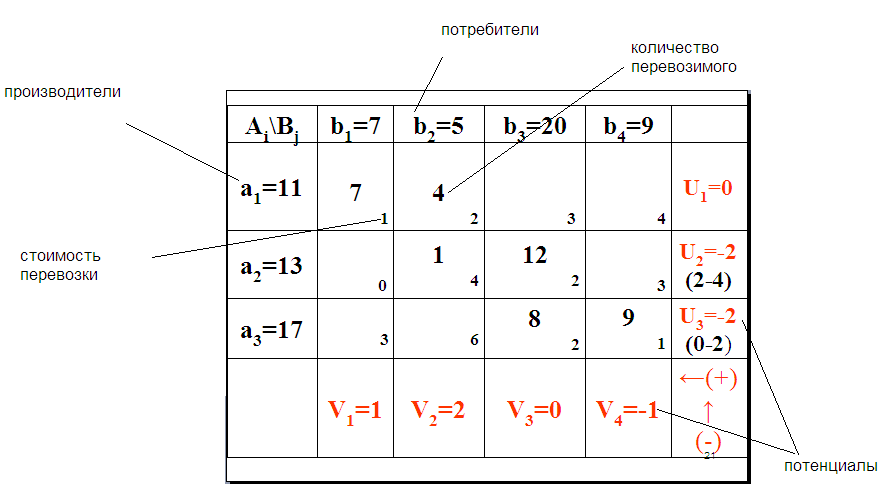
Потенциалы вычисляются из условия:
Vj – Ui = cij для любых базисных i, j
(для клеток с заполненными перевозками).
Для оптимальности плана должно выполняться условие:
Vj – Ui – сij ≤ 0, для любых i,j.
Нарушение признака оптимальности будет в клетке (a2,b1) (говорят -«невязка» в клетке (2,1))
V1 - U2 – с21 =3>0
Туда вводят перевозку!
Убирают:
Среди (1,1) и (2,2) (клеток с «-»)
наименьшее значение «1» в клетке (2,2).
Уменьшаем значения перевозок в клетках цикла, помеченных минусом, на эту минимальную величину и увеличиваем на эту величину значения в клетках цикла, помеченных плюсом.
Удаляем на графе ребро 1-2, пересчитываем таблицу и вновь вычисляем потенциалы.
Всё повторяется до того момента пока не будет невязок.
Значение функции – сумма (количество перевозимого*стоимость перевозки) (для каждой клетки)
Допустимым базисным решением транспортной задачи называется такой набор из m´n неизвестных, который содержит ровно m+n-1, хij>0, неизвестную хij (остальные нули), причем этот набор удовлетворяет условиям (2), (3) и (4).
Оптимальным решением задачи (1)-(4) называется такое допустимое базисное решение, которое дает минимум целевой функции L.