3.4 Определение моментов инерции при повороте координатных осей.

Для сечения A известны моменты в системе координат х у. Новая система координат U, V повернута на некоторый угол α относительно первоначальной. Рассмотрим площадку dA с координатами х, у в первоначальной системе координат. Определим координаты U и V этой площадки в новой системе координат (рис.3.4) используя подобие треугольников:

V=1-2=1-3-2-3=1-3-4-5= (1-5) cosσ - (0-5) sinα = ycosσ – xsinα,

U=0-2=4-2+0-4 = (1-5) sinα + (0-5) cosσ = y sinα + xcosσ.

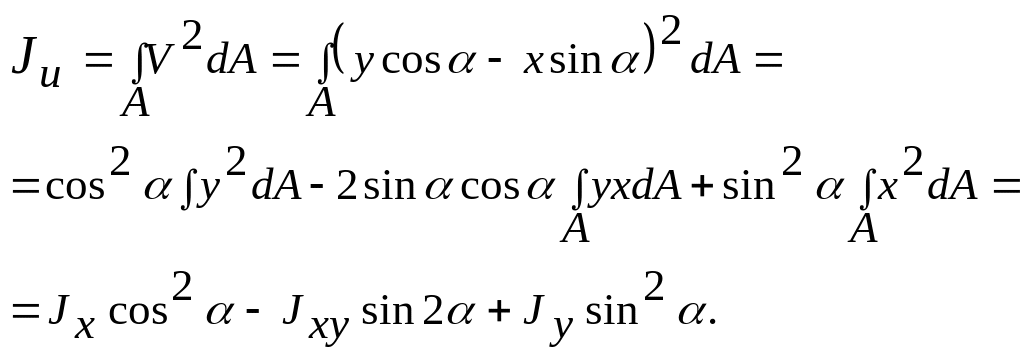
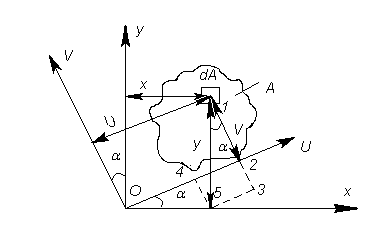
Рис.3.4

Аналогично получим выражение для другой оси:

(3.13)

(3.14)

. (3.15)

после преобразований получим:

(3.16)

С изменением угла поворота значения меняются, а их сумма остается неизменной:

(3.17)

Следовательно, существует такой угол , при котором один из осевых моментов достигает своего максимального значения, а другой – минимального, центробежный момент в таком случае будет равен нулю.

Такие оси называются главными осями инерции, а моменты инерции относительно этих осей называются главными моментами инерции.

Для практических расчетов значение имеют главные оси, которые проходят через центр тяжести сечения, и называются главными центральными осями.

Из выражения (3.16) найдем значение угла .

(3.18)

Положительный угол откладывается против часовой стрелки.

Главные центральные моменты инерции можно определить по формуле:

. (3.19)

Если сечение имеет ось симметрии, то она является главной центральной осью инерции, другая главная центральная ось перпендикулярна ей.

При расчетах стержней на устойчивость пользуются геометрической характеристикой, называемой радиусом инерции сечения, который определяется из равенства:

(3.20)

Радиус инерции равен расстоянию от оси до той точки, в которой следует сосредоточить площадь А (условно), чтобы момент инерции одной этой точки был равен моменту инерции всего сечения.

(3.21)

3.5 Моменты инерции элементарных фигур.

Покажем в качестве примера вычисление интеграла (3.5) для прямоугольника высотой h и шириной b (рис.3.5). Проведем через его центр тяжести О оси симметрии Oz и Оу. Найдем относительно этой оси момент инерции J_x:

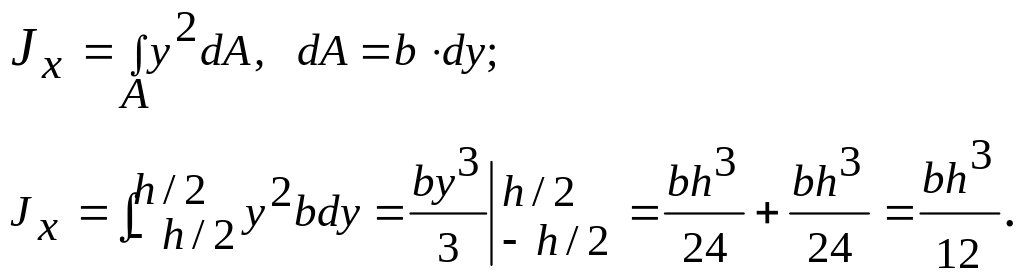
. (3.22)

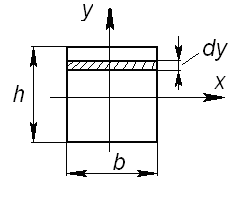
Рис 3.5 Определение осевого момента инерции прямоугольника

Поскольку для прямоугольного сечения оси x, y являются осями симметрии, т.е. главными осями, то .

Для треугольника оси х у так же главные центральные оси (рис.3.6):

(3.23)

Рис.3.6

Определим моменты инерции круга относительно его центра тяжести. Для этого выделим из круга элементарное кольцо толщиной , радиусом (рис.3.7).

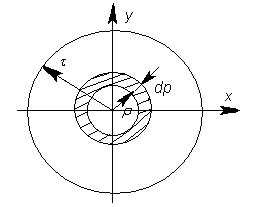
Рис.3.7

Его площадь составляет: , а полярный момент инерции определится как:

. (3.24)

Так как оси х, y являются главными центральными осями , то J_x = J_y,:

. (3.25)

Для полукруга:

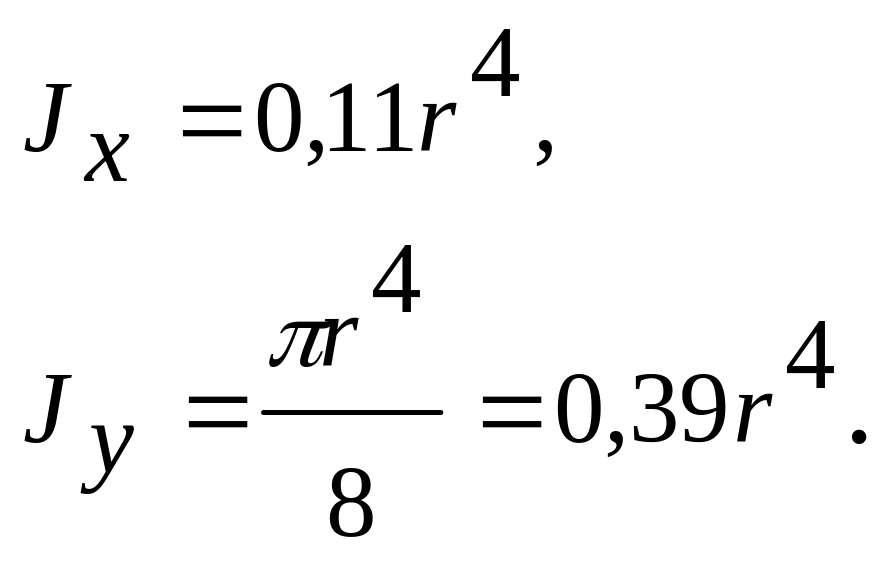(3.26)