МІНІСТЕРСТВО ОСВІТИ І НАУКИ, МОЛОДІ ТА СПОРТУ УКРАЇНИ

Національний університет “Львівська політехніка”

ІКНІ

Методичні вказівки до лабораторної роботи № 13

Градієнтний метод числової оптимізації задач нелінійного програмування.

з дисципліни

“Математичні методи дослідження операцій”

для студентів бакалаврського напряму “Комп’ютерні науки”

Львів – 2011

Методичні вказівки до лабораторної роботи № 13 “ Градієнтний метод числової оптимізації задач нелінійного програмування." з дисципліни “Математичні методи дослідження операцій” для студентів напряму “Комп’ютерні науки” /Укл. Дронюк І.М., Балич Б.І. – Львів: Національний університет «Львівська політехніка», 2011.

Укладач: Дронюк І.М., канд. фіз.-мат. наук, доцент каф. АСУ

Балич Б.І., старший викладач каф. АСУ

.

Відповідальний за випуск: Обельовська К.М., канд. техн. наук, доцент каф. АСУ

Рецензент: Цмоць І.Г., докт. техн. наук, професор каф. АСУ

Лабораторна робота № 13. Градієнтний метод числової оптимізації задач нелінійного програмування.

Мета роботи: ознайомлення з градієнтним методом числової оптимізації, набуття навиків розв’язку та аналізу задач нелінійного програмування градієнтним методом.

Короткі теоретичні відомості

Градієнтні методи належать до наближених числових методів розв’язування задач нелінійного програмування, оскільки дають точний розв’язок за нескінченне і лише в окремих випадках за скінченне число кроків. З їх використанням можна розв’язувати будь-яку задачу нелінійного програмування, знаходячи, як правило, лише локальний екстремум. Тому застосування цих методів дає найбільший ефект для розв’язування задач випуклого програмування, де локальний екстремум є одночасно і глобальним.

1.1. Застосування градієнтного методу, коли обмеження на область зміни змінних х відсутні

Розглянемо задачу максимізації функції f(х), коли обмеження на область зміни змінних х відсутні. Пошук екстремального значення функції f(х) можна починати з будь-якого допустимого розв’язку, наприклад, з точки х_k = (x_1k; ...; х_пk).

Градієнтом f(x) функції f(х) в точці х_k називається вектор, координатами якого є значення в цій точці частинних похідних першого порядку відповідної змінної, тобто

Градієнт функції в цій точці вказує напрямок найшвидшого зростання функції f (х).

Переміщення з точки х_k вздовж градієнту в нову точку х_k+1 відбувається по прямій, рівняння якої

. (1)

де _k – числовий параметр, від величини якого залежить довжина кроку переміщення . Величина _k, при якій досягається найбільший приріст функції, може бути визначена з необхідної умови екстремуму функції

(2)

Чергову точку х_k+1 визначаємо після обчислення параметру _k (для цього підставляємо значення _k в формулу (1) на пошуковій траєкторії). В цій ( х_k+1 ) точці знову знаходимо градієнт, а рух відбувається далі по прямій х_k+2 = х_k+1 + _k+1f(x_k+1) у напрямку нового градієнту f (x_k+2) до точки х_k+2, в якій досягається найбільше значення функції f(х) в цьому напрямку і т.д. Розв’язування триватиме доти, поки не буде досягнута точка х*, в якій градієнт функції дорівнює нулю. В цій точці х* цільова функція f(х*) і буде набувати максимального значення.

Приклад 1. Нехай потрібно визначити точку максимуму функції , коли процес розв’язування розпочинається з точки x₀ = (4;4).

Розв’язування. Знайдемо частинні похідні функції f(x)

; .

Градієнт функції в точці х₀ буде

.

Перемістимось з точки х₀ вздовж градієнту  f(x₀) в нову точку х₁:

х₁ = (4; 4) + ₀ (–6; –4) = (4 – 6 ₀; 4 – 4 ₀).

Градієнт функції в точці х₁ дорівнює

f(x₁) = [2 – 2 (4 – 6₀); 4 – 2 (4 – 4₀)] = (– 6 +12₀; – 4 + 8₀).

З необхідної умови екстремуму одержуємо рівняння

,

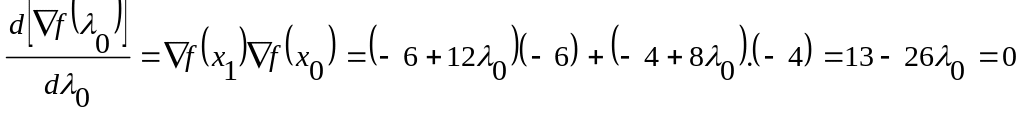звідки = 0,5.

Оскільки , то знайдене значення x₁ є точкою максимуму функції f (x₀).

Враховуючи = 0,5, визначимо координати точки х₁ на пошуковій траєкторії

х₁ = (4 – 6·0,5; 4 – 4·0,5) = (1; 2)

та градієнт f (x₁) в цій точці х₁ f (x₁) = (2 – 2·1; 4 – 2·2) = (0; 0).

Оскільки градієнт f (x₁) має нульові координати, робимо висновок про те, що х₁ = (1; 2) є точкою, в якій цільова функція досягає максимального значення f(х₁) = 2·1+ 4·2 – 1– 4 = 5 (в початковій точці f(х₀) = – 8). На мал. 1 наведена графічна інтерпретація даної задачі.

Мал. 1.