ТЕма 4. Теория однократного рассеяния.

Тематический план:

• Переход от уравнения Гельмгольца к интегральному уравнению для поля. Его решение в виде ряда теории возмущений по малым флуктуациям диэлектрической проницаемости.

• Корреляционная функция и средняя интенсивность поля.

• Дифференциальное и полное (интегральное) сечение рассеяния.

• Пределы применимости теории однократного рассеяния.

• Приближение однократного рассеяния для электромагнитных волн.

• Рассеянные электрическое и магнитное поля в зоне Фраунгофера.

• Вектор Пойнтинга.

• Сечение рассеяния векторного поля.

• Рассеяние линейно- и эллиптически поляризованного поля.

Учебная информация:

Случайные неоднородности реальных сред влияют на характе­ристики поля, распространяющихся в этих средах, и возникающие при этом явления чрезвычайно разнообразны. Мерцание звезд и флуктуации радиоизлучения от внеземных источников, замирания (фединги) радиоволн и релеевское рассеяние света, уширение лазерных пучков в тропосфере и рассеяние звука в море — это лишь немногие примеры наблюдаемых эффектов. Исследованием такого рода эффектов занимается статистическая теория распро­странения и рассеяния воли.

Задачи о распространении волн в средах с флуктуирующими параметрами решаются, как правило, приближенными методами. Дело в том, что соответствующие дифференциальные уравнения содержат в коэффициентах случайные функции точки (а возможно, и времени), описывающие неоднородную среду. Точное решение такой параметрической задачи означало бы, что мы в состоянии написать, например, функцию Грина для любых реализаций входящих в уравнения случайных функций, что практически никогда не осуществимо. Это и вынуждает обращаться к при­ближенным методам. Характер приближения зависит, разумеется, от постановки задачи — слабо или сильно флуктуируют параметры среды, каково соотношение между длиной волны и размерами неоднородностей, какова геометрия задачи (длина трассы, ширина волнового пучка) и т. д. При всем разнообразии конкретных условий значительная часть задач типа 2) может быть решена при помощи небольшого числа разработанных к настоящему времени приближенных методов.

Если относительные флуктуации параметров среды достаточно слабы, а рассеянное поле мало по сравнению с полем первичной волны, то применяется метод малых возмущений. Анализ полей, рассчитанных в первом порядке теории возмущений, составляет содержание теории однократного рассеяния, которой и посвя­щена данная глава.

При нарушении условий применимости теории однократного рассеяния (флуктуации в среде недостаточно слабы, рассеянное поле не мало) необходимо принимать во внимание двух-, трех- и т. д. кратное рассеяние поля, т. е. нужно строить теорию с учетом многократного рассеяния волн. В случае слабых, но крупных (по сравнению с длиной волны) неоднородностей мно­гократно рассеянные волны лишь незначительно уклоняются от направления распространения первичной волны. В таких условиях многократное расселине эффективно описывается методом геомет­рической оптики (МГО) и примыкающими к нему более общими ко­ротковолновыми асимптотическими методами теории дифракции — методом плавных возмущений (МПВ) и методом параболического уравнения (МПУ).

Другая возможность учета многократного рассеяния волн основана на приближенном суммировании рядов теории возму­щений (в основном при помощи методов, развитых первоначально и квантовой электродинамике). При таком подходе удается, в частности, рассмотреть не только слабые, но и сильные флуктуации среды. Однако при этом необходимо, чтобы неоднородности были мелкомасштабными.

Начнем с простейшей постановки задачи: волновое поле u(t, r) будем считать скалярным и монохроматическим (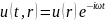 ), а неоднородности среды — неменяющимися со вре­мени и покоящимися. Хотя при скалярной постановке задачи не охвачена поляризация, она достаточна для ряда общеволно­вых явлений, таких, как интерференция и дифракция.

При указанных выше условиях распространение волны в неоднородной среде описывается уравнением Гельмгольца

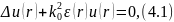
где — волновое число в невозмущенной среде или в слу­чае электрического поля — в вакууме. Функцию 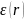, описываю­щую неоднородность среды, мы будем называть (диэлектрической) проницаемостью, имея в виду в основном электромагнитное поле. Для случайно-неоднородной среды проницаемость можно представить в виде

где 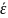— среднее (по ансамблю реализаций среды) значение 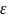, а 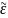— флуктуации проницаемости. Уравнение Гельмгольца при­нимает при этом вид^.

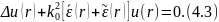
Общих методов решения даже такого простого волнового уравнения не существует. Наиболее распространенным из при­ближенных методов является метод возмущений: флуктуации считаются достаточно слабыми, а волновое поле ищется в виде ряда по степ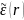еням , или, что то же — по степеням 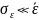. Чтобы построить такой ряд, удобно перейти от дифференциаль­ного уравнения (4.3) к эквивалентному интегральному уравнению.

Пусть 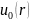— поле первичной волны, удовлетворяющее не­возмущенному уравнению Гельмгольца, т. е. уравнению (4.3) при :

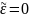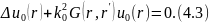
Обозначим через невозмущенную функцию Грина, ко­торая удовлетворяет уравнению для точечного источника

Разумеется, первичное поле и₀ и функция Грина G удовлетво­ряют необходимым граничным условиям. Решение неоднородно­го уравнения

выражается через функцию Грина следующим образом:

Записав исходное уравнение (4.3) в форме

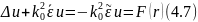
и используя (4.6), получаем следующее интегральное уравнение для волнового поля:

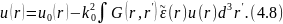
где интегрирование распространяется, очевидно, на область V, занятую неоднородностям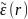и . Уравнение (4.8) эквивалентно исходному дифференциальному уравнению (4.3), но учитывает (через функцию G) и все граничные условия задачи.

Ряд теории возмущений cтроится путем итерирования интег­рального уравнения (4.8). Чтобы получить первую итерацию, запишем значение поля в точке :

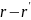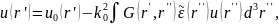
и подставим это выражение в правую часть (4.8). Это дает

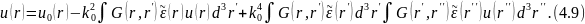
Записав значение поля 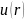в точке 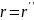и подставив его в правую часть (4.9), получим вторую итерацию. Повторяя такую операцию, мы и получим бесконечный ряд теории возмущении:

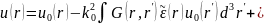
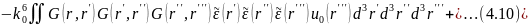
В математике этот ряд называется рядом Неймана для интеграль­ного уравнении (4.8), а в физике — борновским разложением.

Первый член борновского ряда (4.10) — первичное поле . Второе слагаемое,

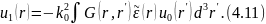
описывает однократно рассеянное поле. Оно порождено непосред­ственно первичным полем и линейно относительно возму­щений . Третье слагаемое в (4.10) можно представить в форме, аналогичной (4.11):

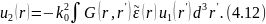
Это — двукратно рассеянное поле, порожденное уже не первичным, а однократно рассеянным полем. Двукратно рассеянное ноле в свою очередь возбуждает трехкратно рассеянные волны 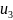, и т. д. Таким образом, ряд теории возмущений (4.10) представляет со­бой разложение рассеянного поля no кратности рас­сеяния:

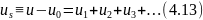
Из самого способа построения этого ряда видно, что n-й его член, описывающий n-кратное рассеяние, содержит под знаком n-кратного интеграла произведение . Отсюда следует, что для вычисления даже среднего значения поля надо знать для моменты любого порядка. При произволь­ной статистике нахождение таких моментов само по себе пред­ставляет сложную задачу, но если даже она и разрешима (как, например, в случае нормального распределении), то остается еще открытым вопрос о методах суммирования усредненных рядов теории возмущений. Здесь же мы ограничимся более простой задачей нахождения статистических характеристик поля в приближении однократного рассеяния (так называемое первое борновское или, чаще, просто борновское приближение).

В этом приближении флуктуации предполагаются настоль­ко малыми, что в разложении (4.13) можно ограничиться первым членом . В данном случае в качестве заданных источников выступает правая часть уравнении (4.7) с 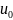вместо и: 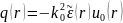. Таким образом, в приближении однократного рассеяния задача о распространении волн в случайно-неоднородных средах (задача типа 2)) сводится к задаче типа 1) — возбуждению полей задан­ными случайными источниками.

Согласно (4.11) рассеянное поле 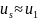является линейным функционалом от флуктуации . Поэтому и все моменты поля , линейно же выражаются через моменты е того же порядка. В частности, у однократно рассеянного поля среднее значение равно нулю, поскольку 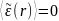_, а корреляционная функция 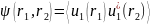линейно выражается через функцию корреляции неоднородности :

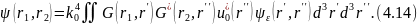
Выражение (4.14) и аналогичные квадратуры для высших моментов рассеянного поля в принципе дают полное статисти­ческое решение задачи в рассматриваемом борновском прибли­жении. Однако этот математический результат еще нуждается в физическом истолковании.

Для того чтобы лучше уяснить основные закономерности рас­сеяния, сделаем ряд допущений, которые упрощают анализ, по вместе с тем сохраняют общность, достаточную для многих при­ложений теории. Допущения сводятся к следующему.

а) Среда в среднем однородна, т. е. — const.

б) Первичное поле представляет собой ненаправленную сферическую волну с центром в точке r₀:

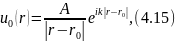
где k—волновое число в однородной среде: .

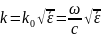в) Функция Грина описывает поле точечного источника в неограниченной однородной среде:

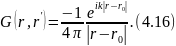
г) Поле флуктуации статистически квазиоднородно, т. е. корреляционная функция имеет вид

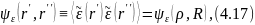
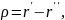
где 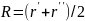и зависимость 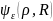от R «медленна», т. е. масштаб изменения 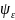по аргументу R существенно больше, чем характерный масштаб 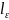(радиус корреляции 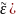по разностному аргументу ρ. Спектральная плотность таких флуктуаций, определяем выражением

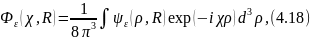
— медленная функция R, т. е. она мало меняется на рассто­яниях порядка .

д) Наконец, будем считать, что случайные неоднородности заполняют ограниченный объем V и в этом объеме содержится много неоднородностей. Последнее условие можно записать в виде неравенства

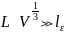или , (4.19)

где L — поперечный размер области, занятой неоднородностями.

Предположение о конечности рассеивающего объема необходимо для обеспечения малости однократно рассеянного поля, тогда как неравенство (4.19) принято лишь дли упрощения расчетов. Конечность рассеивающего объема удобно учитывать при по­мощи обрезающей функции

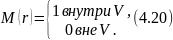
Введя ее под знак интеграла в (4.11), можно распространить интегрирование на вес пространство. Для первичной сферической волны (4.15) и функции Грина свободного пространства (4.16) однократно рассеянное поле (4.11) запишется в виде

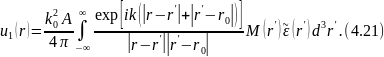
В дальнейшем мы обратимой к некоторым более общим по­становкам задачи (учет временных изменений , расчет поляри­зационных характеристик электромагнитного поля и др.). Вместе с тем мы будем иногда вводить частные допущения (плоская первичная волна, статистически однородные флуктуации и т. д.). Здесь же, исходя из (4.21), мы получим выражения дли функции корреляции и, в частности, для средней интенсивности рассеян­ного поля.

Согласно (4.21) пространственная функция корреляции поля равна

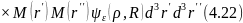
От выражения (4.14) эта формула отличается только тем, что в ней конкретизированы вид первичного поля в вид функции Грина.

Перейдем в (4.22) к переменным интегрирования 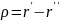, , откуда , 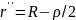. причем .

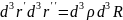Формула (4.22) принимает вид

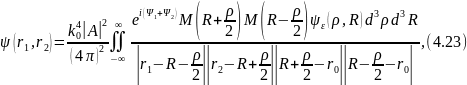
где

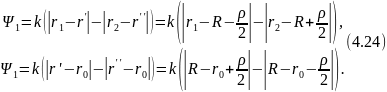
Все последующие упрощения формулы (4.23) основаны на том, что функция корреляции неоднородной среды стано­вится при 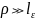очень малой. Мы можем, поэтому воспользоваться разложением модуля вектора 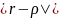ряд Тейлора по степеням малого отношения :

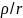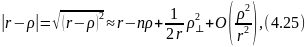
где n = r/r – единичный вектор, а 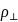- перпендикулярная к n составляющая :

При рассеянии электромагнитных волн (как и при рассеянии поперечных упругих волн) возникают два новых эффекта, кото­рые отсутствуют в скалярной задаче. Во-первых, рассеяние сопровождается изменением поляризации волны, а во-вторых, если речь идет об анизотропной среде, может происходить транс­формации одних типов поляризации в другие. Мы рассмотрим однократное рассеяние электромагнитных волн лишь в изотроп­ной недиспергирующей среде, в которой могут распространяться волны только одного типа, а именно поперечные электромаг­нитные волны.

Рассеяние монохроматических электромаг­нитных волн па покоящихся неоднородностях в изотропной среде. В этом случае уравнения Максвелла

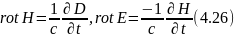
нужно решать совместно с материальным уравнением для изо­тропной недиспергирующей среды

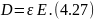
Материальное уравнение (4.27) исключает из рассмотрения не только рассеяние в анизотропных средах, но и рассеяние на анизотропных флуктуациях в изотропной среде (так называемые флуктуации анизотропии). Такие флуктуации возникают, напри­мер, в вязких жидкостях из-за случайных поворотов молекул, если последние оптически анизотропны.

Пусть монохроматическая волна распространяется r среде с постоянной средней диэлектрической проницаемостью и с по­коящимися неоднородностями:

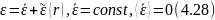
Уравнения Максвелла принимают вид

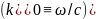
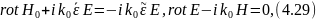
а их решение может быть представлено при слабых флуктуациях 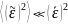рядами теории возмущений

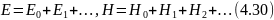
При этом первичное поле Е₀, Н₀ удовлетворяет однородным уравнениям

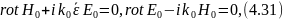
а однократно рассеянное поле — неоднородным уравнениям

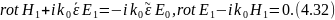
Уравнения для последующих приближений получаются из (4.32) при последовательных заменах .

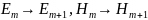Рассеянные поля Е₁, и Н₁ можно найти, используя известные функции Грина, т. е. решение задачи о возбуждении электромаг­нитных воли точечным электрическим источником 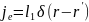. В волновой зоне, т. е. при 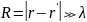, элементарный источник создает поля

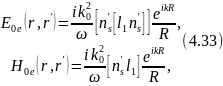
где 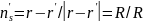— единичный вектор, направленный из r' в r.

Используя (4.33), решение неоднородных уравнений (4.32) можно представить в виде

Так как существенно новое по сравнению со скалярной задачей касается только поляризации рассеянного поля, рассмотрим простейший случай, когда точка наблюдения расположена в зоне Фраунгофера рассеивающего объема (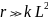 ), а первичное поле представляет собой плоскую волну:

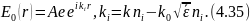
Здесь е — вектор поляризации первичной волны, вообще говоря — комплексный. Будем считать его нормированным к единице условием ее* = 1. В силу поперечности волн, распространяю­щихся в изотропной среде, вектор поляризации перпендикулярен к направлению распространения п_i. Простой расчет с использованием разложений вида (4.11) дает для однократно рассеянных полей Е₁ и Н₁ выражения

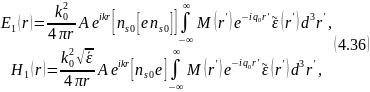
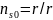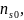
где — единичный вектор, направленный в точку г из центра рассеивающей области, a — вектор рассе­яния, отвечающий центру этой области. Для упрощения записи мы опустим ниже индекс 0 у векторов и

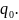
Легко видеть, что поля E₁ и Н₁ отличаются от скалярного поля

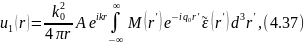
вычисленного при тех же допущениях, только множителями:

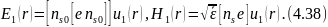
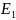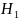Следовательно, в приближении однократного рассеяния при де­терминированной поляризации е первичной волны любые средние билинейные величины, составленные из компонент полей и могут быть выражены через функцию корреляции скаляр­ного поля . Если же поляризация пер­вичного поля случайна, то усреднения по направлениям е и по ансамблю неоднородности е производятся раздельно в силу ста­тистической независимости этих величин. Иными словами, и при случайной поляризации первичной волны средние от билинейных комбинаций компонент и можно выразить через или .

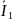Средний вектор Пойнтинга и эффективный поперечник рассеяния. Среди билинейных комбинаций, составленных из компонент и важную роль играет вектор Пойитинга

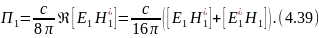
Учитывая, что

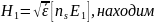
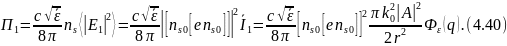
Введем эффективный поперечник рассеяния единицы объема в единичный телесный угол 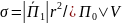, где 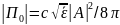— модуль плотности потока энергии первич­ной волны. При помощи (4.15) находим

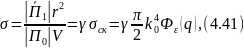
где 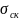— «скалярный» поперечник рассеяния. Множитель

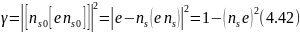
связан с особенностями рассеяния электромагнитных волн по сравнению со скалярной задачей и может быть назван поляриза­ционным.

Для линейно поляризованной первичной волны е — вещественный единичный вектор. Если χ — угол между е и n_s, то 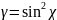. Таким образом, для линейно поляризованной первичной волны

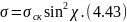
Множитель 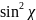обращается в нуль в направлениях, коллинеарных с e, что связано с дипольным характером рассеяния электро­магнитных волн в каждом элементе рассеивающего объема.

Произвольную эллиптически поляризованную волну можно пред­ставить, как известно, в виде суммы двух линейно поляризованных колебаний, сдвинутых по фазе на π /2. Пусть большая ось эллипса и соляризации направлена вдоль орта e₁, а малая — вдоль орта e₂. Векторы e₁ и e₂ ортогональны к направлению распро­странения 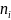, так что e₁, e₂ и , образуют ортогональную связку. При эллиптической поляризации

где p₁ и p₂ — вещественные коэффициенты, удовлетворяющие, в силу принятой нами нормировки ее* = 1, условию

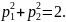
Зная 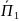, нетрудно найти эффективный поперечник (сечение) рассеяния σ единичного объема в единичный телесный угол в на­правлении n_S.

По определению

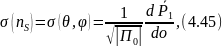
где 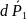—средняя мощность, рассеиваемая в телесный угол do в направлении V — рассеивающий объем, а 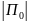— модуль плот­ности потока энергии в первичной волне. Через θ и 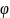обозна­чены полярный и азимутальный углы, отвечающие направлению 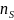(рис. 4).

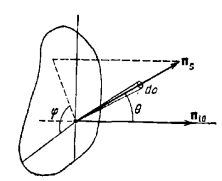
Рис. 4

Мощность равна

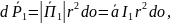
или,

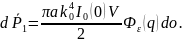
Плотность же потока энергии в первичной волне, будь то пло­ская, сферическая или направленная сферическая волна равна (по модулю) 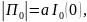так что (4.45) даёт

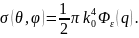
Если корреляцион­ная функции 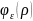отличается от нуля только в малой области 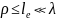. В этом случае мелкомасштабных неоднородностей рассеяние изотропно:

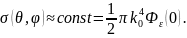
Напротив, в случае крупномасштабных неоднородностей (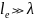 ) спектральная плотность 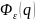быстро уменьшается с ростом q, т. е. с ростом угла рассеяния θ, что отвечает преимущественному рассеянию вперед. Сектор углов θ, в котором сосредоточено излу­чение, можно оценить из условия 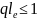или . Ниже мы проиллюстрируем этн особенности рассеяния несколькими при­мерами.

Величину (4.45) называют также дифференциальным сечением рассеяния — в отличие от полного поперечника рассеяния

Рис. 5

Поляризационный множитель γ для волн эллиптической поля­ризации равен

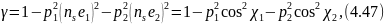
где χ ₁ и χ ₂—углы между вектором n_s, и ортами е₁ и е₂, (рис. 5). Подставляя (4.47) в (4.41) и учитывая, что , по­лучаем

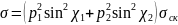
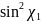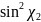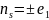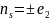В отличие от линейно поляризованной первичной волны, сечение никогда не обращается в нуль, потому что и , не могут обратиться в нуль одновременно. Из (4.38) следует, что в направлениях и , рассеянное поле поляризовано линейно — и силу уже отмечен­ного дипольного характера рассеяния. В других направлениях рассеянное поле поляризовано по эллипсу. Параметры эллипса поляризации могут быть найдены из выражений (4.38), если в них подставить (4.42).

В частном случае круговой поляризации волны, когда 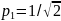, 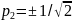(плюс отвечает правой, а минус — левой поляризации), находим из (4.43)

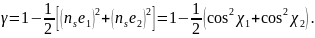
В силу взаимной ортогональности векторов e₁, е₂, и n_i, имеем 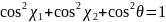так что для волну поляризованных по кругу,

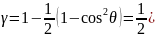
Таким образом, γ зависит здесь только от угла рассеяния θ, т. е. имеет азимутальную симметрию.

Если в точке наблюдения r измеряется интенсивность рассе­янных волн какой-либо одной поляризации, то плотность потока энергии будет, очевидно, меньше плотности полного по­тока (4.41) и, соответственно, уменьшится величина эффектив­ного сечения рассеяния σ.

Вопросы для самоконтроля по теме:

1. Приведите примеры наблюдаемых эффектов того, как случайные неоднородности реальных сред влияют на характе­ристики поля, распространяющихся в этих средах.

2. Граница применимости теории однократного рассеянья.

3. Какие допущения делаются в теории однократного рассеянья.

4. В каком случае неоднородность называется мелкомасштабной или крупномасштабной.

5. Напишите уравнения Максвелла в дифференциальной форме.

6. Запишите основное выражение для вектора Пойнтинга.

7. Найдите эффективный поперечник (сечение) рассеяния σ единичного объема в единичный телесный угол в на­правлении n_S.