7.3 Циклические коды

Циклическим кодом называется линейный блочный код 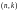, который характеризуется свойством цикличности, то есть сдвиг влево на один шаг любого разрешенного кодового слова дает другое разрешенное кодовое слово, принадлежащее этому же коду; множество кодовых слов циклического кода представляется совокупностью полиномов степени и менее, делящихся на некоторый полином 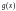степени . Полином является сомножителем двучлена и называется порождающим (или производящим). Длина кодового слова определяется как 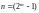, где –расширение поля .

Кодирование циклического кода осуществляется делением информационной последовательности на . Поэтому для формирования кода достаточно знать производящий полином , который определяется как наименьшее общее кратное (НОК) произведения минимальных функций ,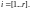 Имеются также таблицы полиномов в специальной литературе.

Производящая матрица циклического кода определяется путем умножения 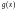степени ( 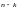) последовательно на 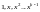. Первая строка проверочной матрицы определяется выражением 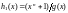, остальные – умножением первой строки на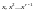 . Проверочная матрица позволяет вычислить синдром ошибки в виде полинома степени

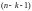
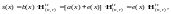(7.16)

Для циклических кодов операция вычисление синдрома ошибки может быть также записана в виде

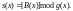
Помимо основных циклических кодов существует подкласс укороченных циклических кодов, которые образуются путем уменьшения числа информационных символов. Они имеют те же свойствами, что и основной коды.

Лучшими циклическими кодами, обеспечивающими эффективную борьбу с независимыми ошибками, являются циклические коды Боуза–Чоудхури–Хоквингема (БЧХ).

В качестве примера на рис.7.2 приведена структурная схема кодера циклического кода БЧХ (15,11) над полем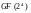 , производящий полином кода 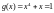. Кодер представляет собой двоичный регистр сдвига с обратной связью через сумматоры по , которые расположены в позициях, определяемых видом производящего полинома.

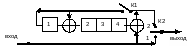
Рис. 7.2  Кодер циклического кода (15,11)

Кодирование производится за 15 тактов. В течение первых 11 тактов ключ К1 замкнут, ключ К2 находится в положении 1; происходит вычисление проверочных символов в регистре сдвига путем деления информационных символов на производящий полином, одновременно информационные символы через ключ К2 подаются на выход кодека. В течение последующих 4 тактов ключ К1 разомкнут, ключ К2 в положении 2; происходит считывание на выход кодера проверочных символов из ячеек регистра сдвига.

При декодировании кодового слова циклического кода также производится его деление на производящий полином. Наличие остатка (синдрома ошибки) указывает на искажение слова. Для анализа синдрома с целью поиска конфигурации ошибок могут использоваться те же методы, что и для обычных групповых кодов. Простейший из них использует таблицу синдромов всех исправляемых ошибок, а оценка ошибки находится путем сравнения вычисленного синдрома с имеющимися в таблице. Недостатком таких декодеров является быстрое увеличение количества синдромов с увеличением кратности исправляемых ошибок. Циклические коды позволяют уменьшить объём таблицы синдромов.

В качестве примера рассмотрим декодер Меггита для циклического кода (15.11), исправляющий ошибки кратности единица. В нем хранится только один синдром ошибки: 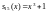(соответствует полиному ошибок 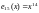). Синдромы остальных одиночных ошибок циклически сдвигаются в регистре синдрома до совпадения с 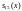; число циклов сдвига плюс единица равно номеру искаженного кодового символа. Поэтому такие декодеры иногда называются декодерами с вылавливанием ошибок. Структурная схема декодера показана на рисунке 7.3.

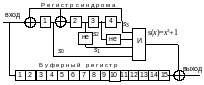
Рис.7.3 – Декодер Меггита для циклического кода (15,11)

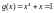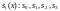
Декодер работает следующим образом. Кодовое слово (с ошибками или без них) в виде последовательности из 15 двоичных символов поступает в буферный регистр и одновременно в регистр синдрома, где производится деление этого слова на производящий полином , в результате чего вычисляется синдром ошибки  элементы синдрома. Ошибка обнаруживается, если хотя бы один элемент синдрома не равен нулю. Исправление ошибок производится в следующих 15 циклах сдвига. В каждом -ом цикле проверяется равенство 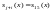и в благоприятном случае на выходе схемы “И” появляется импульс коррекции ошибки, инвертирующий символ на выходе буферного регистра.

Для исправления ошибок большой кратности, как правило, используются методы субоптимального декодирования, которые позволяют упростить декодер при незначительном снижении качества: исправление ошибок производится, как правило, в пределах гарантируемой кодом кратности (7.5). К этим методам относятся перестановочные, алгебраические (мажоритарный, пороговый и пр.) и некоторые другие.

Перестановочные методы декодирования основываются на свойстве симметрии циклических кодов, т. е. на существовании такого множества перестановок элементов декодируемой кодовой последовательности, которые переводят ее в последовательность, принадлежащую тому же коду. Можно найти такую перестановку, в результате которой на информационных позициях будут находиться только неискаженные элементы.

К числу методов, использующих для декодирования алгебраические особенности линейных кодов, относится мажоритарный (пороговый) метод декодирования циклических кодов. Этот метод применим только для тех циклических кодов, для которых может быть образована система ортогональных (разделенных) проверок для каждого символа принятого сообщения. Каждая -я строка проверочной матрицы задает одно соотношение, связывающее между собой символы кодового слова (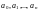 ). Набор этих соотношений называется контрольными проверками, на основе которых формируется система ортогональных (разделенных) проверок, удовлетворяющих следующим требованиям:

• число проверочных соотношений должно быть ;

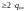• проверяемый символ 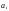входит в каждую проверку;

• любой другой символ 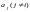входит лишь в одну из проверок.

При выполнении этих условий ошибка в проверяемом символе искажает все проверки, а ошибка в символе искажает только одну проверку, что позволяет принимать решение о значении символа по большинству проверок.

Универсальным алгебраическим методом декодирования кодов БЧХ является формирование уравнения локатора ошибок, указывающего позиции ошибок в декодируемом кодовом слове. Если код является двоичным, то этого достаточно для исправления ошибок. В случае недвоичных кодов необходимо дополнительно найти уравнение значения ошибки в каждой позиции.

Структурная схема декодера кодов БЧХ показана на рис. 7.4.

Рис. 7.4 – Структурная схема алгебраического декодера кода БЧХ

Для определения позиций и значения ошибок в этих позициях необходимо найти корни уравнений локаторов и значений ошибок. Для формирования уравнения локатор ошибок применяются два алгоритма: алгоритм Берликэмпа–Месси и алгоритм Евклида. Оба эти алгоритма используют преобразование Фурье над конечным полем, что позволяет построить декодер как во временном, так и в частотном пространствах.

Структурная схема алгоритма Берликэмпа–Месси в частотном пространстве приведена на рисунке 7.5.

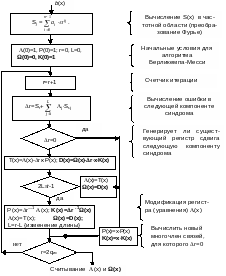
Рис.7.5 Алгоритм Берликэмпа–Месси в частотном пространстве

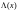Для недвоичных кодов БЧХ кроме уравнения локатора ошибок необходимо также найти уравнение значений ошибок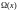 . В частотном пространстве

,

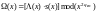и последовательность полиномов 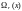, удовлетворяет тем же рекуррентным соотношениям, что и полиномы 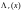. На рис. 7.5 промежуточный регистр, необходимый для формирования , обозначен 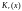.Тогда

.

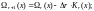
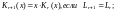
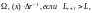На рисунке 7.5 эта часть алгоритма выделена жирным шрифтом.

Формирование уравнений локатора ошибок и значений ошибок начинается с преобразования Фурье (вычисления спектра декодируемого кодового слова 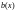). Задача формирования уравнения локатора ошибок эквивалентна задаче построения регистра сдвига минимальной длины, генерирующего первые 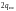элемента полинома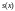 , которые являются элементами синдрома ошибки в частотном пространстве. Вначале строится самый короткий регистр сдвига, генерирующий 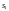по 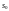с учетом начальных условий. Затем проверяем, генерирует ли этот регистр также и 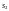(вычисляется поправка 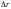); если да, то регистр не меняется и продолжается проверка генерирует ли он следующие элементы ; если нет, то нужно изменить регистр так, чтобы он правильно генерировал следующий элемент. Процесс продолжается до тех пор, пока не будут сформирован регистр, генерирующий первые элементов .

Алгоритм Берликэмпа–Месси можно преобразовать так, чтобы исключить преобразование Фурье в начале декодера. При этом учитывается то обстоятельство, что рекурсия по всем входным полиномам этого алгоритма линейна, и можно использовать их представление во временном пространстве. В результате алгоритм превращается во временном пространстве в рекуррентный процесс, который описывается следующей теоремой.

Теорема 7.1 Пусть 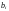- символы принятого слова кода БЧХ, и пусть величины 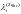, 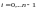вычисляются с помощью рекуррентных уравнений

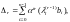
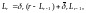
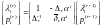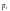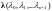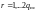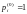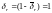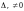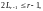, где – промежуточный регистр; – ошибка воспроизведения; - вектор локатора ошибок; , начальные условия имеют вид , для всех , а , если одновременно и и 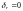в противном случае; тогда 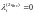, тогда и только, когда 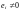(в отличие от частотного представления полиномы 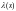, и пр. обозначены малыми буквами).

Структурная схема декодера двоичных кодов БЧХ с использованием алгоритма Берликэмпа–Месси во временном пространстве показана на рис. 7.6.

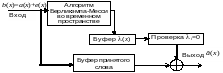
Рис.7.6 Структурная схема декодера двоичных кодов БЧХ

Декодер двоичных циклических кодов по схеме рис. 7.6 работает быстрее, так как нет необходимости определения корней уравнения локатора ошибок.

Построение недвоичных ( -ичных) кодов БЧХ мало отличается от построения двоичных кодов и сводится к определению производящего полинома , который либо неприводим, либо представляет собой произведение неприводимых полиномов.

Важным и широко используемым подклассом недвоичных циклических кодов БЧХ являются коды Рида-Соломона (коды РС). Для этих кодов компоненты кодовых слов и их преобразования могут находиться как в двоичном поле, так и в -ичном поле 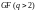. В дальнейшем будем рассматривать только коды РС над двоичным полем .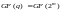

Производящий полином кода РС определяется просто

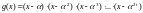, (7.17)

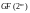где - примитивный элемент поля , а длина -ичного кодового слова равна .

Коды РС применяются для исправления ошибок и стираний в каналах с пакетирующимися ошибками и в качестве внешнего кода при каскадном кодировании в аппаратуре радиорелейной, сотовой и космической связи с учетом того, что после декодирования внутреннего кода ошибки группируются. Важной его особенностью является то, что этот код имеет кодовое расстояние

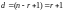(7.18)

и является кодом с максимальным кодовым расстоянием. Поэтому коды РС всегда оказываются короче всех других циклических кодов над тем же алфавитом и являются оптимальными с точки зрения эффективности использования избыточности, так как максимальная кратность исправляемых ошибок равна половине проверочных символов в -ичном кодовом слове.

Кодирование кода РС производится так же, как и любых циклических кодов: проверочные символы образуются как остаток от деления -ичной информационной последовательности на производящий полином. Это может быть сделано с помощью -ичного регистра сдвига, который может быть реализован на двоичных регистрах с обратными связями, определяемыми коэффициентами производящего полинома, либо программно.

В общем случае декодирование кодов РС является существенно более сложной процедурой, чем двоичных циклических кодов, так как необходимо определить не только позиции ошибок, но и их величину в соответствии со структурной схемой, показанной на рисунке 7.4. В частном случае для исправления ошибок малой кратности может быть построен декодер с вылавливанием ошибок (декодер Меггита для кодов РС).

Оценка вероятности ошибок декодирования кодов РС в каналах с независимыми ошибками (вероятность ошибки ) может быть вычислена по формуле:

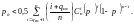(7.19)

Коэффициент 0,5 перед суммой учитывает среднее число искаженных двоичных символов в -ичных символах декодируемого слова кода РС.