
7.4 Свёрточные коды
Сверточными кодами являются непрерывные древовидные коды, для которых справедлива линейная свертка:
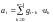 или
в виде полиномов
или
в виде полиномов
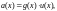 где
где
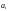 –
символы кода,
–
символы кода,
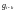 –
весовые коэффициенты (значения разрядов
производящего полинома
–
весовые коэффициенты (значения разрядов
производящего полинома
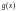 ),
),
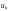 – информационные символы кодовой
последовательности
– информационные символы кодовой
последовательности
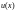 .
.
Сверточные
коды, которые иногда называют скользящими
блочными кодами,
обычно задаются скоростью
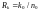 и,
в отличие от блочных кодов, требуют для
своего описания несколько порождающих
(производящих) полиномов. Эти полиномы
могут быть объединены в матрицу
и,
в отличие от блочных кодов, требуют для
своего описания несколько порождающих
(производящих) полиномов. Эти полиномы
могут быть объединены в матрицу
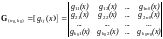 , (7.20)
, (7.20)
где
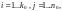
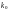
число информационных символов, необходимых
для формирования одного кадра
из
число информационных символов, необходимых
для формирования одного кадра
из
 символов
на выходе кодера.
символов
на выходе кодера.
Длина
скользящего слова
 и его информационная часть
и его информационная часть
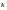 при
данной скорости
при
данной скорости
 определяются размером кадра и максимальной
степенью производящих полиномов
определяются размером кадра и максимальной
степенью производящих полиномов
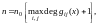
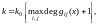
Вместо
длины кодового слова часто используется
понятие «длина
кодового ограничения»
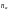 ,
которая показывает максимальное
расстояние между позициями информационных
символов, участвующих в формировании
проверочного символа кода
,
которая показывает максимальное
расстояние между позициями информационных
символов, участвующих в формировании
проверочного символа кода
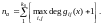 (7.21)
(7.21)
Проверочная
матрица
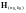 должна удовлетворять условию
должна удовлетворять условию
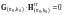 ,
а вектор синдромов ошибки (синдромных
полиномов) равен
,
а вектор синдромов ошибки (синдромных
полиномов) равен
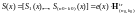 ,
т.е.
,
т.е.
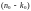 -мерный
вектор-строка из полиномов.
-мерный
вектор-строка из полиномов.
В
дальнейшем будут рассматриваться только
двоичные сверточные коды, для которых
сложение и умножение полиномов
производится над двоичным полем. Если
сверточный код является систематическим,
то
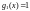 ;
тогда (при
=1)
;
тогда (при
=1)
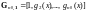 ,
а для кодов
,
а для кодов
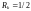 ,
,
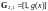 .
.
Сверточные
коды, скорость которых
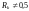 ,
позволяют либо увеличить скорость кода
,
позволяют либо увеличить скорость кода
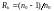 за счет потери корректирующей способности,
либо увеличить корректирующую способность
а за счет уменьшения скорости
за счет потери корректирующей способности,
либо увеличить корректирующую способность
а за счет уменьшения скорости
 .
Причем существует двойственность между
этими кодами, что позволяет использовать
для их построения одинаковые порождающие
полиномы.
.
Причем существует двойственность между
этими кодами, что позволяет использовать
для их построения одинаковые порождающие
полиномы.
Качество
работы декодера зависит также от длины
блока декодирования (ширины окна декодирования); причем, чем
больше блок декодирования, тем лучше.
Это определяется тем, что сверточный
код имеет множество минимальных
расстояний, которые определяются длинами
начальных сегментов кодовых
последовательностей, между которыми
определяется минимальное расстояние
в процессе декодирования. Это расстояние
равно
(ширины окна декодирования); причем, чем
больше блок декодирования, тем лучше.
Это определяется тем, что сверточный
код имеет множество минимальных
расстояний, которые определяются длинами
начальных сегментов кодовых
последовательностей, между которыми
определяется минимальное расстояние
в процессе декодирования. Это расстояние
равно
 –числу
ненулевых символов в блоке декодирования
с ненулевым первым кадром. При этом
декодер может исправить
–числу
ненулевых символов в блоке декодирования
с ненулевым первым кадром. При этом
декодер может исправить ошибок, если
ошибок, если
 .
Для большинства хороших сверточных
кодов длина блока декодирования может
быть ≥
.
.
Для большинства хороших сверточных
кодов длина блока декодирования может
быть ≥
.
Свободным
кодовым расстоянием
сверточного кода называется расстояние
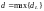 .
Как правило, свободное кодовое расстояние
для двоичных сверточных кодов при
определяется выражением:
.
Как правило, свободное кодовое расстояние
для двоичных сверточных кодов при
определяется выражением:
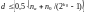 . (7.22)
. (7.22)
Кодирование сверточных кодов производится аналогично блочным циклическим кодам с помощью регистров сдвига, у которых структура обратных связей определяется производящим полиномом кода. Различие только в том, что сверточный код может иметь несколько производящих полиномов и кодер должен иметь соответствующее число регистров сдвига.
На
рисунке 7.7 приведены функциональные
схемы двух кодеров для сверточных кодов
(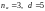 )
и
)
и
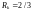 (
( ).
Эти коды являются несистематическими;
производящие полиномы кода
представлены
на рисунке.
).
Эти коды являются несистематическими;
производящие полиномы кода
представлены
на рисунке.
Кодеры работают следующим образом. На вход регистра сдвига кодера (а) из 3 ячеек памяти подается двоичные информационные символы, из которых с помощью регистра сдвига и сумматоров по модулю 2 формируется две двоичных последовательности. Этих последовательности переключателем П поочередно подключаются к выходу кодера.
Матрица производящих полиномов кода R=2/3 имеет вид:
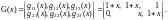
Регистры сдвига ( регистров) кодера б) имеют по две ячейки памяти и три сумматора ( сумматоров), формирующих символы кода в соответствии с видом производящих полиномов. Переключатель П1 разделяет входные кодовые символы между регистрами, переключатель П2 формирует кодовую последовательность на выходе.
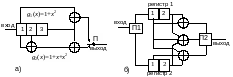
Рис. 7.7 – Кодеры сверточных кодов а) и б)
Кодовое дерево рассматриваемого кода , и соответствующая кодовая решетка имеют вид, показанный на рис. 7.8.
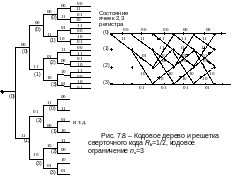
Кодовое
дерево строится таким образом, что
информационному символу «0» соответствует
перемещение на верхнюю ветвь (ребро)
дерева, а информационному символу «1»
на нижнюю ветвь. Можно обратить внимание,
что после формирования четырех вершин
(на рис. 7.8 отмечены цифрами 0,1,2,3 в скобках)
структура ветвей дерева повторяется.
Это обстоятельство определяется
состоянием двух последних ячеек памяти
регистра сдвига кодера (00,01,10,11); в общем
случае число состояний зависит от
кодового ограничения кода и равно
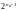 .
.
Решетка сверточного кода представляет состояния кодера в виде четырех уровней, а ветви дерева являются ребрами решетки, в результате чего избыточные части дерева отождествляются. Такое представление кода является более удобным при разработке и описании процессов декодирования.
Для декодирования сверточных кодов используются, в основном, три метода: декодирование по алгоритму Витерби, синдромное декодирование и последовательное декодирование.
Декодирование по алгоритму Витерби и последовательное декодирование являются оптимальными по критерию максимального правдоподобия (МП) и широко используются для двоичных сверточных кодов с малой длиной кодового ограничения.
Методы синдромного декодирования могут оптимизироваться по критерию МП и основаны на вычислении и последующем анализе синдрома ошибок, что делает их похожими на соответствующие методы декодирования циклических кодов.
Рассмотрим алгоритм Витерби на примере исправления ошибок сверточным кодом , кодер, кодовое дерево и кодовая решетка которого показана на рис. 7.7 и 7.8.
Предположим,
что передавалось нулевая кодовая
последовательность вида {00 00 00 00 …}, а
принятая последовательность на выходе
демодулятора с жестким решением имеет
вид{10 00 10 00 00 …} (произошло две ошибки).
Такая конфигурация ошибок должна
исправляться, поскольку кодовое
расстояние данного кода
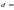 5.
Ниже показана серия решетчатых диаграмм,
показывающих состояние решетки после
2, 3, 9 и 10 циклов алгоритма. Числа,
поставленные в вершинах, указывают
расстояние Хэмминга (выделены жирным
шрифтом), накопленное «выжившим» путем
в этой вершине;«выжившие» пути показаны
сплошными линиями, «невыжившие» пути
– пунктиром. Ребра графа обозначены
двойными цифрами обычным шрифтом. На
первом и втором шагах алгоритма (диаграмма
а)) произошла первая ошибка в канале и
«выжившими» являются все 4 пути. На
третьем шаге произошла вторая ошибка
в канале (диаграмма б)), каждый из путей
раздвоился и сохранился лишь лучший
путь, метрика которого в меньшей степени
отличается от принятой последовательности
(показана в нижней части каждого рисунка).
5.
Ниже показана серия решетчатых диаграмм,
показывающих состояние решетки после
2, 3, 9 и 10 циклов алгоритма. Числа,
поставленные в вершинах, указывают
расстояние Хэмминга (выделены жирным
шрифтом), накопленное «выжившим» путем
в этой вершине;«выжившие» пути показаны
сплошными линиями, «невыжившие» пути
– пунктиром. Ребра графа обозначены
двойными цифрами обычным шрифтом. На
первом и втором шагах алгоритма (диаграмма
а)) произошла первая ошибка в канале и
«выжившими» являются все 4 пути. На
третьем шаге произошла вторая ошибка
в канале (диаграмма б)), каждый из путей
раздвоился и сохранился лишь лучший
путь, метрика которого в меньшей степени
отличается от принятой последовательности
(показана в нижней части каждого рисунка).
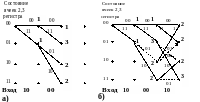
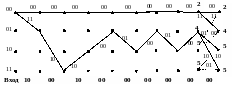
в)

г) Рис. 7.9
Общее число сохранившихся путей вновь становится равным 4 по числу вершин графа. Этот процесс повторяется после приема следующей пары символов.
Выживающие пути могут отличаться друг от друга в течение большого числа шагов алгоритма (диаграмма в)). Однако на десятом шаге (диаграмма г)) первые восемь ребер всех выживших путей совпадают. В этот момент можно принимать решение о переданных информационных символах на первых шагах алгоритма (на выход выдается самый старый символ выжившего пути).
Основные
трудности при реализации алгоритма
Витерби определяются тем, что сложность
декодера экспоненциально растет с
увеличением кодового ограничения (число
состояний декодера равно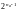 );
поэтому значение кодового ограничения
кодов, применяемых на практике, не
превышает
);
поэтому значение кодового ограничения
кодов, применяемых на практике, не
превышает
 .
Недвоичные коды декодировать алгоритмом
Витерби еще сложнее.
.
Недвоичные коды декодировать алгоритмом
Витерби еще сложнее.
В кодеках сверточных кодов с декодированием по алгоритму Витерби, в основном, используются несистематические коды, так как они позволяют при малом кодовом ограничении получить большее свободное расстояние. Декодирование по алгоритму Витерби кода (кодер на рис. 7.7б) оказывается существенно сложнее по сравнению с кодами . В каждую вершину кодовой решетки будет входить теперь не два пути, а четыре и для определения выживших путей необходимо производить восьмеричное сравнение.
В отличие от алгоритма Витерби при последовательном декодировании производится продолжение и обновление метрики только одного пути, который представляется наиболее вероятным, при этом делается попытка принять решение о декодируемом символе, принятом в начале пути. Если решение о декодируемом символе, находящемся в начале пути, принять невозможно, то производится либо движение вперед, т.е. прием очередного символа и обработка метрики данного пути, или возврат назад (выбор другого пути), если значения метрики увеличиваются. Процедура продолжается до тех пор, пока не будет принято решение о декодировании символа, расположенного в начале пути.
Основное достоинство последовательного алгоритма заключается в том, что в среднем длина пути, достаточная для правильного декодирования меньше, чем у алгоритма Витерби. Недостатки определяются тем, что длина пути, приводящего к правильному декодированию, является случайной величиной. Это вызывает затруднения при реализации декодера, так как всегда существует вероятность переполнения памяти и сбой декодера.
Практически используются, в основном, два метода синдромного декодирования: декодирование с табличным поиском, и пороговое декодирование. Наиболее перспективными в смысле благоприятного сочетания качества декодирования и сложности реализации являются пороговые (в частных случаях мажоритарные) алгоритмы декодирования сверточных кодов. В сочетании с кодами, имеющими малую плотность проверок на четность, пороговые алгоритмы и итерационные пороговые алгоритмы являются более гибкими в каналах с пакетирующимися ошибками.
Пороговое декодирование возможно для относительно ограниченного класса сверточных кодов, позволяющих построить ортогональные проверки относительно проверяемого символа. В настоящее время получено множество хороших кодов, состоящее из канонических самоортогональных кодов (КСОК) и кодов, допускающих ортогонализацию.
Множество
проверок
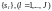 ,
ортогональное относительно символа
ошибки в
-ом
информационном символе, задаётся
множество элементов синдрома. Это
множество для кода
,
ортогональное относительно символа
ошибки в
-ом
информационном символе, задаётся
множество элементов синдрома. Это
множество для кода
 может быть использовано для порогового
(мажоритарного) декодирования в
соответствии с правилом:
может быть использовано для порогового
(мажоритарного) декодирования в
соответствии с правилом:
если
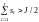 ,
тогда
,
тогда
 = 1, иначе
= 0. (7.23)
= 1, иначе
= 0. (7.23)
Структурная схема порогового декодера, реализующего данное правило решения показана на рисунке 7.10.
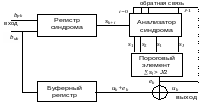
Рис. 7.10 – Структурная схема порогового декодера
Последовательность
символов канала
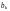 после
разделения на информационные
после
разделения на информационные
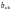 и
проверочные
и
проверочные
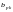 поступает
в регистр синдрома, где производится
вычисление элементов синдрома. В
анализаторе синдрома формируются
ортогональные проверки
поступает
в регистр синдрома, где производится
вычисление элементов синдрома. В
анализаторе синдрома формируются
ортогональные проверки
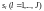 ,
сумма которых в пороговом устройстве
сравнивается с уровнем порога и
определяется значение символа ошибки
,
сумма которых в пороговом устройстве
сравнивается с уровнем порога и
определяется значение символа ошибки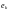 .
Исправление ошибки происходит в сумматоре
по модулю два, на второй вход которого
подаются информационные символы канала
из буферного регистра, выполняющего
функцию хранения этих символов на время
вычисления символа ошибки.
.
Исправление ошибки происходит в сумматоре
по модулю два, на второй вход которого
подаются информационные символы канала
из буферного регистра, выполняющего
функцию хранения этих символов на время
вычисления символа ошибки.
Для
кодов
 число
проверочных соотношений
число
проверочных соотношений
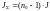 ,
а кодовое расстояние
,
а кодовое расстояние
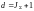 .
Кодовое расстояние для кодов
.
Кодовое расстояние для кодов
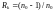 определяется
как и для
,
т.е.
определяется
как и для
,
т.е.
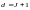 .
Однако, в сравнении с кодом
,
происходит
ухудшение качества декодирования из-за
увеличения числа информационных символов
в проверочных соотношениях.
.
Однако, в сравнении с кодом
,
происходит
ухудшение качества декодирования из-за
увеличения числа информационных символов
в проверочных соотношениях.
К
достоинствам порогового декодера
относится возможность его реализации
на скоростях передачи, практически
равных скорости работы элементной базы,
используемой для построения декодера.
Качество порогового декодера можно
улучшить, если ввести обратную связь
(на рис. 7.10 показана пунктиром), через
которую решение декодера подается в
анализатор синдрома и устраняет влияние
ошибки данного символа на декодирование
следующего символа. При декодировании
с обратной связью кодовое расстояние
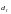 больше,
чем при детерминированном декодировании
(без обратной связи) и ближе к значению
свободного кодового расстояния
больше,
чем при детерминированном декодировании
(без обратной связи) и ближе к значению
свободного кодового расстояния
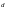 .
.
Вероятность
ошибки декодирования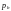 в пороговом декодере минимальна, если
используется правило решения по максимуму
апостериорной вероятности (правило
МАВ). Для двоичного симметричного канала
c вероятностью ошибки
в пороговом декодере минимальна, если
используется правило решения по максимуму
апостериорной вероятности (правило
МАВ). Для двоичного симметричного канала
c вероятностью ошибки
 эта вероятность определяется неравенством:
эта вероятность определяется неравенством:
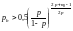 . (7.24)
. (7.24)
В частном случае, когда канал является стационарным на длине кодового ограничения вероятность ошибки декодирования определяется выражением:
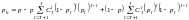 , (7.25)
, (7.25)
где
из вероятности ошибок вычитается
вероятность обнаруженных ошибок и
прибавляется вероятность ложного
обнаружения и исправления ошибок,
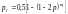 ,
,
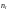 –
объем проверки
–
объем проверки
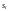 .
.
Следовательно
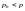 ,
если выполняется неравенство
,
если выполняется неравенство
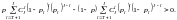
С
учётом того, что
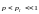 ,
получаем
,
получаем
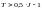 .
Это неравенство показывает, что в
пороговом декодере значение порога
может быть (при достаточно малых
вероятностях ошибки в канале) даже
меньше, чем это требует мажоритарное
правило решения, согласно которому
.
Это неравенство показывает, что в
пороговом декодере значение порога
может быть (при достаточно малых
вероятностях ошибки в канале) даже
меньше, чем это требует мажоритарное
правило решения, согласно которому
 .
.
Основными алгоритмами порогового декодирования сверточных кодов являются непрерывный и блочный алгоритмы. Схемы кодеков могут быть реализованы на регистрах сдвига и логических структурах малой и средней степени интеграции. Для вычисления проверочных символов, синдромов и анализаторов синдромов могут быть использованы специальные БИС, так как эти регистры имеют практически одинаковую структуру, которая определяется видом производящего полинома кода.
