Примеры решения заданий по теме (4)

ПРИМЕР 4.1

В точках и закреплены два заряда и , соответственно.

Определить положение точки , в которой напряженность суммарного электростатического поля зарядов и , равна нулю.

Р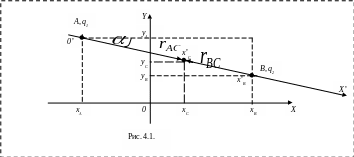 ешение примера 4.1. Рассмотрим ситуацию, изображенную на рис. 4.1.

Вектор напряженности электростатического поля, создаваемого в точке точечным зарядом , находящимся в точке , определяется следующим образом:

,

где , — электрическая постоянная, — вектор, проведенный от точки до точки , — его модуль. Так как вектор можно представить в виде:

,

где и — единичные векторы вдоль осей OX и OY, соответственно, то зависимость от координат вектора напряженности электрического поля, создаваемого зарядом , запишется следующим образом:

.

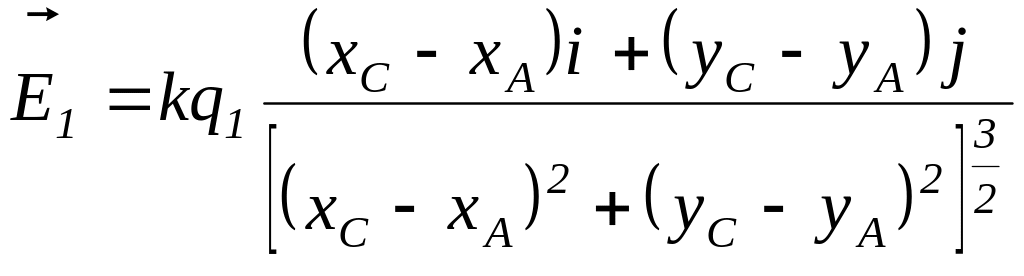Вектор напряженности электростатического поля, создаваемого в точке точечным зарядом , находящимся в точке , определяется аналогично:

.

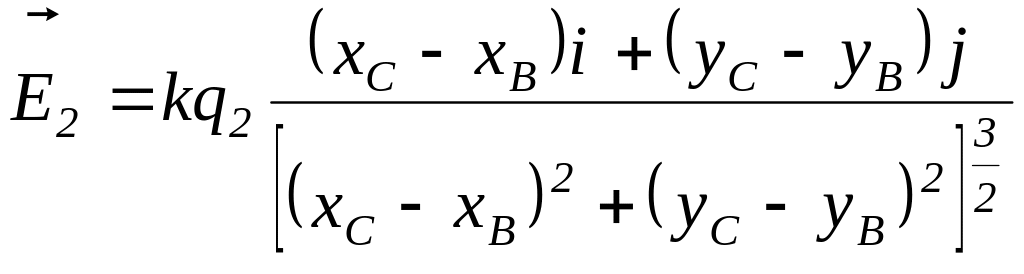По условию задачи, в точке должно выполняться условие:

.

Для этого необходимо, чтобы вектора и были равны по модулю и направлены в противоположные стороны. Приравнивая почленно значения проекций векторов и на оси координат, получим систему уравнений, решение которой позволяет определить неизвестные координаты точки :

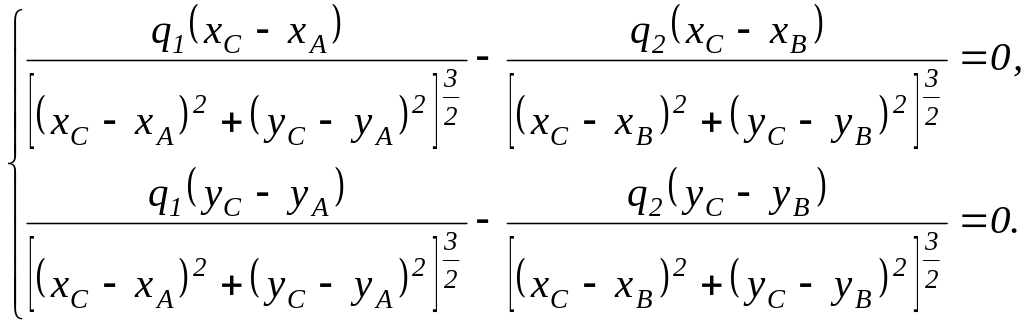
Решение данной системы уравнений упростится, если перейти в систему координат , показанную на рис. 4.1. В новой системе координат система уравнений сводится к одному уравнению:

,

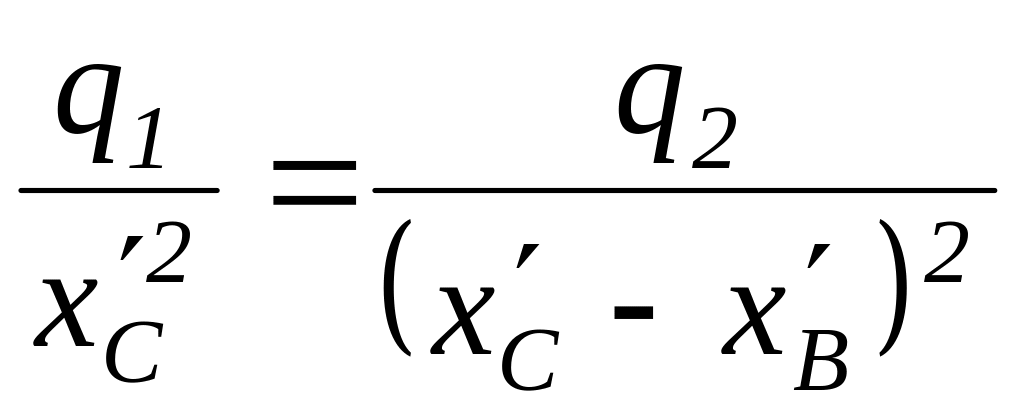где и — новые координаты точек С и В, соответственно. Решение этого уравнения дает следующее значение координаты :

.

Координата равна расстоянию между точками и :

.

Обратный переход осуществляется по формулам, определяемым из рис. 4.1:

,

,

.

ПРИМЕР 4.2

Контур , в виде квадрата со стороной , размещают так, чтобы заряд оказался на пересечении диагоналей квадрата, а его стороны располагают параллельно осям координат.

2. Найти разность потенциалов между ближайшими вершинами квадрата, расположенными вдоль оси ОХ.

Решение примера 4.2.

Разность потенциалов между любыми точками, лежащими на кривой по определению равна криволинейному интегралу вдоль кривой L от скалярного произведения вектора напряженности электрического поля и элемента длины контура:

.

Расположим систему координат так, чтобы заряд находился в начале координат. Тогда вектор напряженности электростатического поля точечного заряда запишется следующим образом:

.

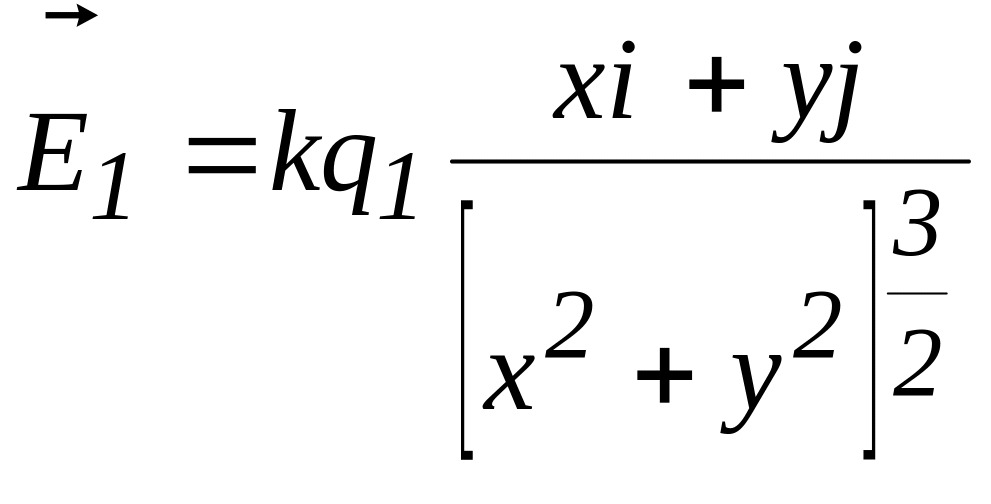Так как вершины квадрата расположены вдоль оси ОХ, то вектор элемента длины контура в данном случае равен:

.

Скалярное произведение запишется в виде:

.

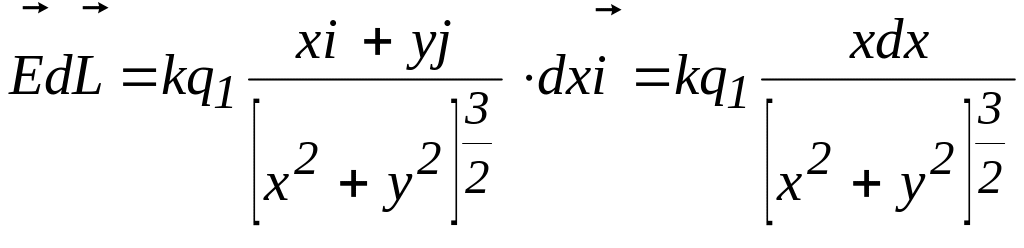Здесь учтено, что скалярное произведение взаимноперпендикулярных векторов и , равно нулю.

Таким образом, разность потенциалов запишется в виде:

.

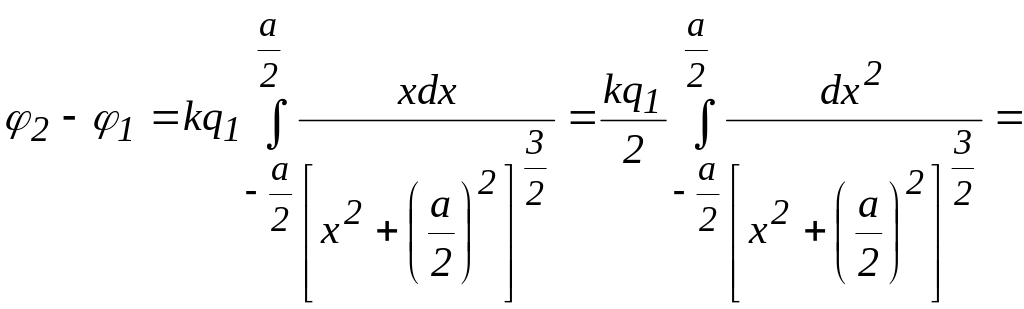
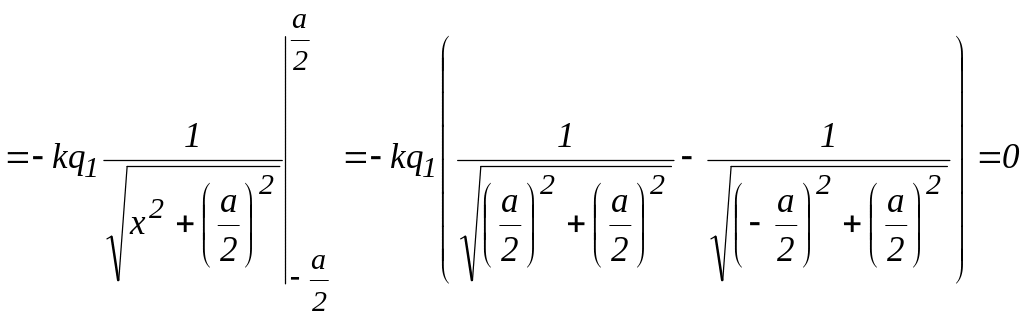ПРИМЕР 4.3

Тонкий равномерно заряженный стержень длиной размещают так, чтобы заряд находился на оси, проходящей вдоль стержня на расстоянии от одного из его концов. Общий заряд стержня равен .

Найти силу, с которой стержень действует на заряд .

Решение примера 4.3.

Для нахождения силы взаимодействия точечного заряда и стержня с таким же по величине зарядом нельзя непосредственно воспользоваться законом Кулона, применимым только к взаимодействию точечных зарядов. Поэтому выделим на стержне достаточно малый участок длиной и зарядом , где — линейная плотность распределения заряда по стержню.

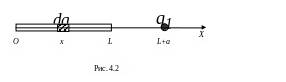
Если заряд достаточно мал, то его можно рассматривать как точечный. Поэтому, для нахождения силы взаимодействия двух точечных зарядов и правомерно применение закона Кулона:

,

где — расстояние между зарядами и .

Интегрируя это выражение в пределах от до , получим выражение для силы, с которой стержень действует на заряд :

.