1. Экструзионный метод наложения изоляции.

Наложение изоляции на провода и кабель явилось одной из первых областей применение экструзии. Схема экструзионной линии для изолирования провода следующая:

1. Отдающее устройство.

2. Выпрямляющее устройство.

3. Подогревающее устройство - обеспечивает ликвидацию влажных и масляных пятен, улучшает адгезию между полимером и жилой.

4. Пластифицирующий экструдер с кабельной головкой - обеспечивает движение, плавление, течение полимера под большим давлением и наложением расплава полимера на жилу или пучок ранее изолированных жил (при наложении оболочки).

5. Охлаждающая ванна.

6. Контролирующие устройства – устройства для проверки толщины изоляции, скорости изолирования, а также счетчик метража и испытательная станция.

7. Тянущее устройство (кабестан).

8. Приёмное устройство.

Полимер наносится на токопроводящую жилу, образуя первичный изолирующий слой. Металлический слой подаётся к фильере с отдающего устройства, проходя по пути в угловую головку через правильник и подогреватель. Изолированный провод выходит из фильеры и попадает в водяную ванну. Затем он проходит электрический контроль, где проверяется целостность изоляции, и поступает на тянущий кабестан, оттуда – к приёмному устройству.

Скорость изоляцирования зависит от типа полимера и диаметра провода. При наложении первичной изоляции из ПЭНП и ПВХ на тонкие провода линейная скорость экструзии на современных зарубежных линиях достигает 1000 – 1500 м/мин. Линии для изоляции кабелей имеют аналогичную конструкцию, но работают при значительно меньших скоростях.

Основным элементом в технологической цепочке процесса наложения изоляции на провода и кабели является пластифицирующий экструдер. Для каждого конкретного провода с определённым диаметром скорость нанесения изоляции будет определяться в значительной мере (на 90%) производительностью экструдера.

Кроме того, нужно отметить тот факт, что сегодня в мировой практике переработке полимеров 40% объема перерабатывается методом экструзии.

Поэтому на сегодняшний день теоретическое описание и изучение работы экструдера (с целью его усовершенствования, повышением производительности и качества изоляции), процессов, протекающих в нём, остаётся актуальной проблемой.

2. Физико-механические основы переработки полимеров.

Явление переноса.

 Прикладная наука о транспортных явлениях рассматривает перенос массы, количества движения и энергии. Она включает в себя те теоретические правила, с помощью которых решают задачи, связанные с течением жидкостей, теплопереносом и диффузией в различных средах.

Рассмотрим основные соотношения теории переноса:

• закон сохранения массы

• закон сохранения количества движения

• закон сохранения энергии

Используя математическую формулировку всех трех законов, получают определяющую систему дифференциальных уравнений в частных производных, которую замыкают условия однозначности, характеризующими конкретный процесс.

 

Уравнение неразрывности.

Простейшие из уравнений баланса – уравнение неразрывности, выражающее закон сохранения массы.

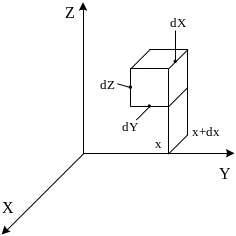
Рассмотрим область пространства в декартовых координатах x, y, z, через которую со скоростью (x,y,z,t) протекает однородная жидкость плотностью (x, y, z, t)*1 . Принцип сохранения массы в фиксированном объеме пространства V=dxdydz может быть записан в виде: (скорость накопление массы в V) =(скорости подвода массы в V)+(скорости отвода массы из V)

Плотность среды в точке определяется пределом отношения:

Разложим вектор скорости: _x (x,y,z,t),_y (x,y,z,t),_z (x,y,z,t)

Рассмотрим – расход материала через единицу площади (количество материала, проходящего через единицу площади в единицу времени в направлении оси x),

Тогда – количество материала, проходящего в единицу времени в направлении оси x через площадку dydz в сечении x,

– количество выходящего материала.

Для остальных координат вводится аналогично.

Разность – то, что осталось внутри объема, тем самым увеличивая плотность:

Если плотность внутри объёма - , то изменение плотности - , тогда скорость накопления массы (на сколько кг в секунду увеличится плотность, ) равна .

Это выражение равно алгебраической сумме потоков массы входящих и выходящих через шесть граней куба:

(1.1)

Каждая скобка в левой части уравнения (1.1) представляет собой чистый приток массы через три главные плоскости куба (диффузионных потоков через поверхность куба нет, поскольку жидкость однородная).

Разделим каждый член (1.1) на элементарный объем dxdydz, при условии, что размеры куба стремятся к нулю, в пределе получим:

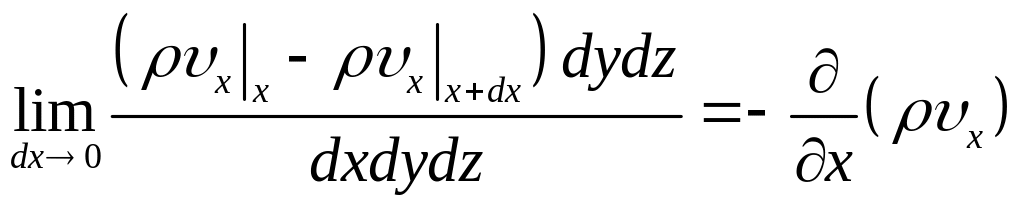^*2 - для координаты x.

(1.2)

Преобразуем левую часть (1.2):

, получим:

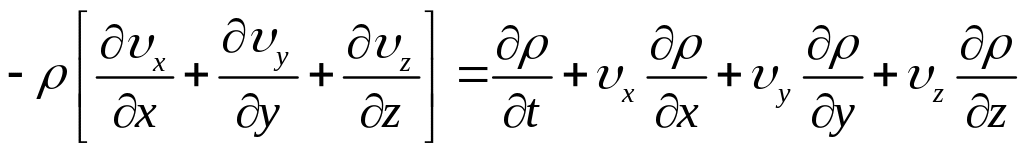(1.2’)

Уравнения (1.2) и (1.2’) называют уравнениями неразрывности.

Будем полагать, что плотность слабо зависит от координат и времени, т.е. не происходит накопления. =const, получим, что производные по =0:

- уравнение несжимаемости. (1.3)

Силы в сплошной среде. Тензор напряжения.

В динамике сплошных сред принято выделять два класса действующих на частицы среды сил: объёмные (иногда их называют массовыми) и поверхностные силы. Под объёмными силами понимают такие, которые действуют на элементы объёма, например, силы веса, притяжения, инерции, силы действия магнитного и электрического поля. К поверхностным относят силы, которые при принятом в механике сплошных сред макроскопическом подходе действуют на элементы поверхности, как, например, силы давления, силы реакции и т.д.

В отличие от динамики сплошных систем дискретных точек (теор. меха), в динамике сплошных сред имеют дело не с самими силами, а с плотностью их распределения в пространстве. Так под объёмной силой F в данной точке M среды понимают предел отношения главного вектора сил, приложенных к точкам малого объёма V, заключающего в себе точку M, к массе m=, а объём стремится к 0, сохраняя внутри себя точку M, т.е.

или

В качестве примера можно указать, что в случае сил веса F=mg, а F_m=g (массовая)

Аналогично поверхностные силы будут задаваться своей плотностью распределения, называемой напряжением.

,

гдеP’ - главный вектор сил, приложенных со сторон среды к некоторой выделенной в среде малой площадки S.

Отметим основное различие между двумя векторамиF иP: в то время как векторF является однозначной векторной функцией точек пространства и времени, т.е. образует векторное поле, векторP принимает в каждой точке пространства бесчисленное множество значений в зависимости от ориентировки площадки, к которой приложено напряжение, и векторное поле не образует.

Таким образом, может показаться, что существует бесконечное количество независимых способов описания напряжённого состояния. Для полного и однозначного описания напряжённого состояния в точке (и в целом в среде) рассматривают тензор напряжений.

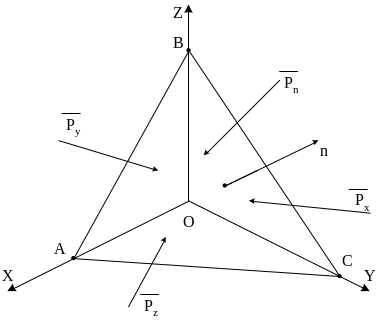
Рассмотрим вырезанный в среде элементарный тетраэдр OABC с вершиной в данной точке O, основанием в виде треугольника ABC, образованного пересечением наклонной плоскости с тремя координатными плоскостями, и боковыми гранями, расположенными в координатных плоскостях.

Обозначим площадь ABC через S_ABC, а площадь треугольников OBC, OAB, OAC, представляющие проекции ABC на координатные плоскости, S_OAC, S_OAB, S_OBC.

– уравновешенная поверхностная сила; – силы, действующие на соответствующие площадки; n – вектор нормали к треугольнику ABC; Пренебрегая действием массовых сил в среде (в рассматриваемом объёме) составляем выражение баланса сил:

(1.4)

Заметим, что

Подставив эти равенства в (1.4) и сократив на S_ABC, получим:

(1.5)

Спроецируем (1.5) на оси декартовых координат:

(*)

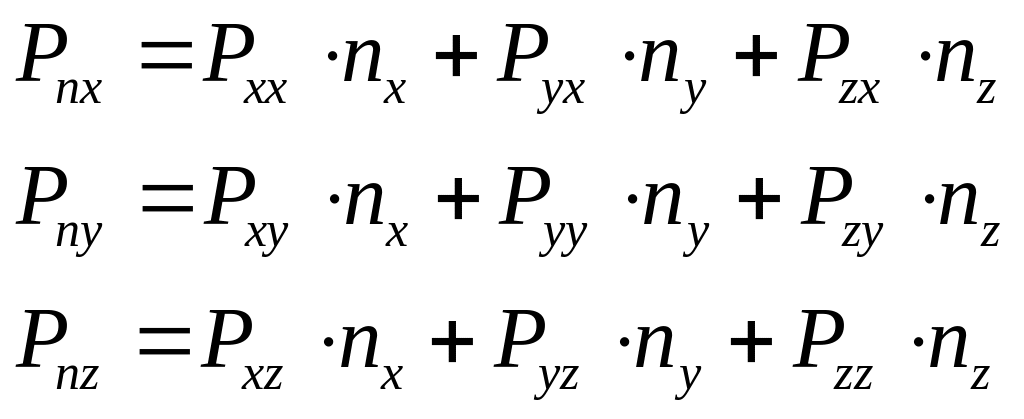При принятых обозначениях первый подстрочный индекс при напряжении P обозначает ось, перпендикулярно которой ориентирована площадка, второй индекс – ось, на которую спроектировано напряжение. ТакP_xz обозначает проекцию на ось z напряжения, приложенного к площадке, перпендикулярной к оси x.

Величины с одинаковыми индексами P_xx, P_yy, P_zz, представляют проекции векторов на нормали к соответствующим площадкам, называются нормальными напряжениями, а остальные – касательные напряжения.

Система равенств (*) показывает, что проекции на оси координат напряжения, приложенного к любой наклонной площадке, выражаются линейно через проекции напряжений, приложенных к трём взаимно-перпендикулярным площадкам, лежащим в координатных плоскостях. Совокупность этих компонент, лежащих в трех взаимно-перпендикулярных плоскостях образуют тензор второго ранга, который и называется тензором напряжения.

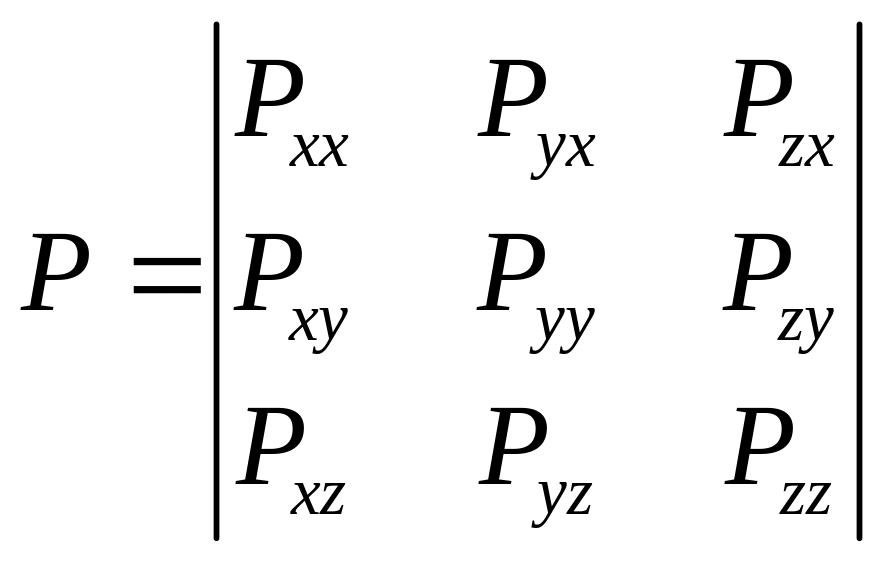
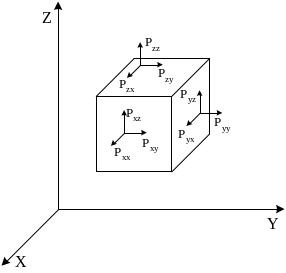
Компоненты тензора напряжений в пространстве располагаются следующим образом:

Таким образом, напряжённое состояние полностью определяется в точке M, если задать компоненты векторов напряжений на трёх взаимно-перпендикулярных плоскостях, проходящих через точку M. Для полного описания напряжённого состояния необходимо знать девять компонент – по три для каждого вектора. Каждую компоненту можно описать двумя индексами i и j. Первый индекс указывает ориентацию площадки, второй направление действия силы.

В задачах механики жидких и твёрдых сред используется закон парности касательных напряжений: , т.е. тензор напряжений является симметричным тензором. Таким образом, для полного описания напряжённого состояния в точке M необходимо знать только шесть независимых компонентов тензора напряжений.

Уравнение движения.

Получают на основе закона сохранения главного вектора количества движения: изменение главного вектора количества движения (K) во времени в объеме dV равно сумме всех сил, приложенных к этому объему.

Приравнивая индивидуальную производную по времени от главного вектора количества движения главному вектору внешних массовых и поверхностных сил, получим:

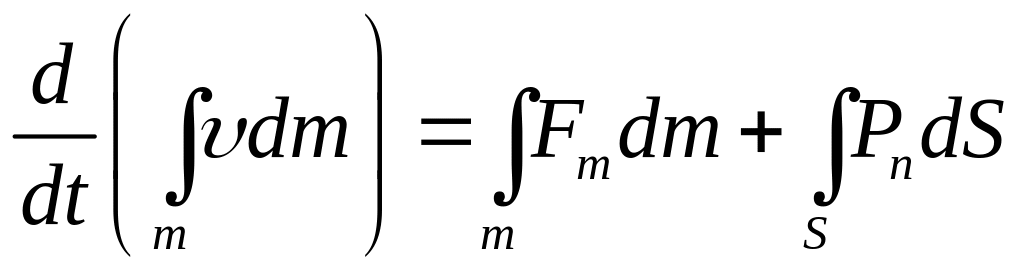
т.к. , а , то получим:

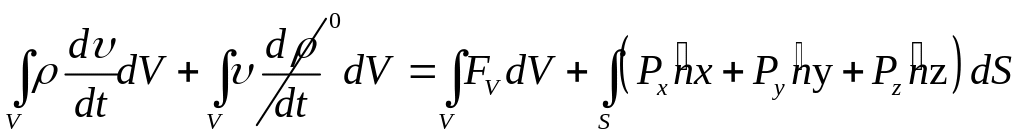(1.6)

В выражении (1.6) будем предполагать, что накопления материала внутри объема не происходит, т.е. =const, а =0.

Для перехода от поверхностного интеграла к объемному используем теорему Остроградского – Гаусса:

Заменяем последний интеграл в выражении (1.6) и сводим всё под один знак интеграла:

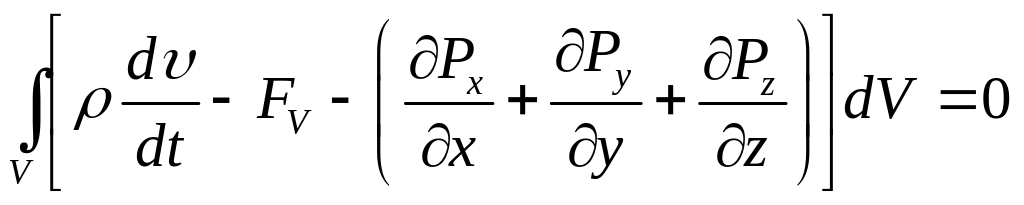
Так как интеграл равен нулю, а dV является малым и виртуальным, то можем приравнять подынтегральной выражение нулю (избавиться от знака интеграла):

Так как массовые силы в рассматриваемых задачах значительно меньше поверхностных, то ими будем пренебрегать: F_V=0:

(1.7)

Спроецируем (1.7) на координатные оси, получим:

так как , то получим:

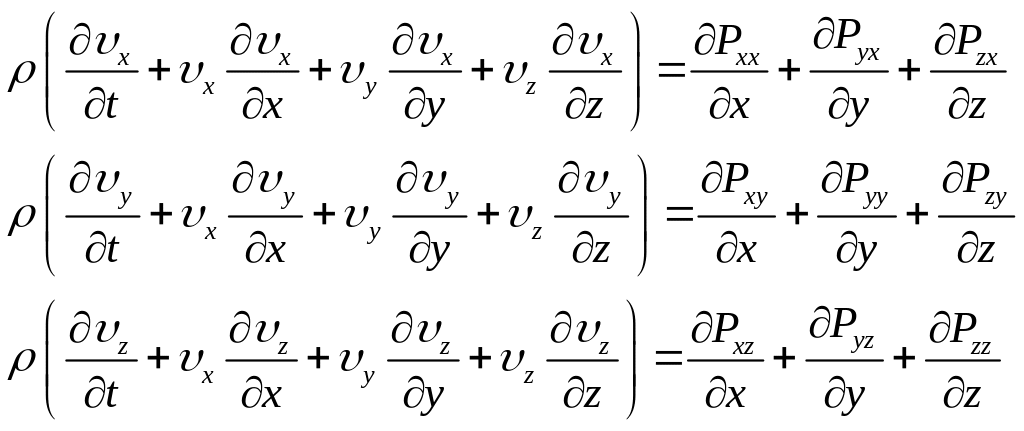(1.8)

Полученные уравнения носят названия – уравнений динамики сплошной среды в напряжениях.

Входящий в уравнение динамики тензор напряжений принято делить на две части и называть полным напряжением.

^*3

где – символ Кронекера;

– шаровой тензор, отвечающий за изменение объема;

– девиатор (девиаторный тензор), отвечает за изменение формы.

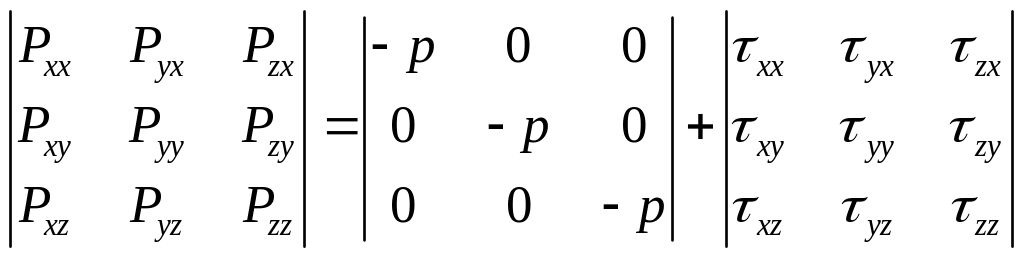(1.9)

С учетом (1.9) правая часть уравнения (1.8) запишется:

Тогда уравнения движения:

(1.10)

Пользуясь численной нумерацией координат, проекций векторов и компонент тензоров, можно представить уравнение (1.10) в компонентной компактной форме:

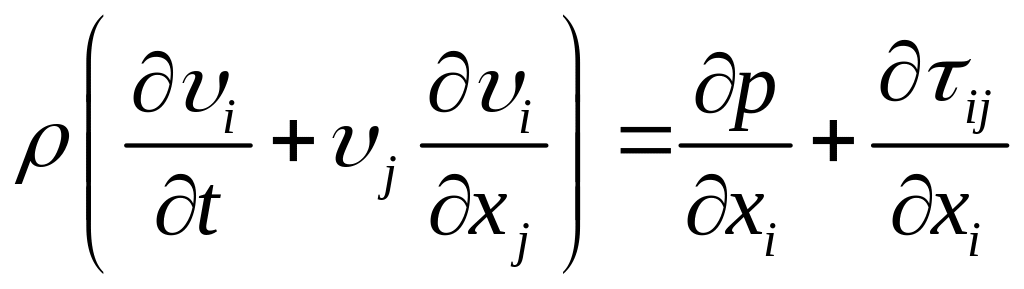(1.11)

Уравнения (1.10) и (1.11) имеют форму второго закона Ньютона. Оно показывает, что скорость изменения количества движения системы равна сумме сил, действующих на неё.

Уравнение энергии.

При выводе этого и предыдущих уравнений используют метод математической физики, который исходит из того, что ограничивается промежуток времени и из всего пространства, выделяется лишь элементарный объём. Это позволяет в пределах элементарного объёма и малого отрезка времени пренебречь изменением некоторых величин и существенно упростить задачу.

Выбранные таким образом элементарные и с математической точки зрения являются величинами бесконечно малыми, а с физической точки зрения – величинами ещё достаточно большими, чтобы в их пределах можно было бы игнорировать дискретное строение среды и рассматривать среду как эталонную.

При выводе дифференциального уравнения энергии делают следующие допущения:

- материал однородный и изотропный;

- теплофизические характеристики постоянны;

- внутренние источники тепла распределены по объему равномерно.

В основу вывода дифференциального уравнения теплопроводности положен закон сохранения энергии, который в рассматриваемом случае может быть сформулирован таким образом:

Количество тепла, подведенное к элементарному объёму dV за время d (это dQ*), равно изменению внутренней энергии вещества (dU), содержащегося в данном объёме:

, (1.12)

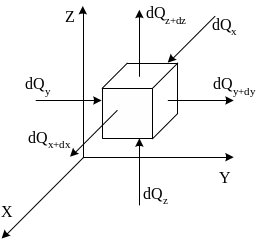
Для нахождения составляющих уравнения (1.12) выделим в теле параллелепипед со сторонами dx, dy, dz. Грани параллелепипеда параллельны соответствующим координатным плоскостям. Количество теплоты, которое подводится к граням элементарного объёма за время d в направлении осей Ox, Oy, Оz, обозначим dQx, dQy, dQz, Общее количество тепла извне:

Введем понятие потока тепла: – количество тепла, проходящего в единицу времени через единицу площади (в данном случае в направлении оси Ox),

– поток, проходящий через сечение x

– поток, проходящий через сечение x+dx

Разница между количеством теплоты, подведённого к dV за d и отведённого в направлениях O_x, O_y, O_z может быть выражено:

(1.13)

Функция считается непрерывной в рассматриваемом объёме и может быть разложена в ряд Тейлора:

(1.14)

Достаточно только два первых члена ряда, подставим (1.14) в (1.13), получим:

Общее количество теплоты, подведённое к dV за d:

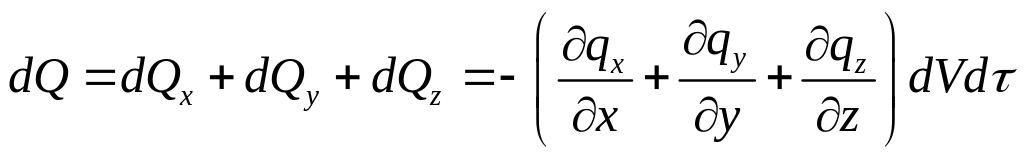
Определим вторую составляющую уравнения (1.12):

Обозначим количество теплоты, выделяемое внутренними источниками в единице объёма среды за единицу времени и называемое мощностью внутренних источников тепла, через , тогда:

;

Третья составляющая уравнения (1.12) находится для изохорного процесса:

,

где с – теплоемкость^*4;  – плотность;

Запишем уравнение (1.12) со всеми изменениями:

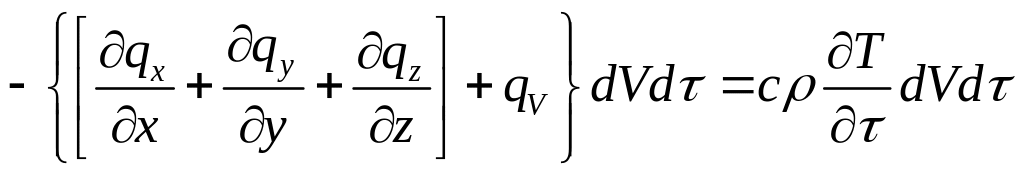
или, после сокращения на dVd

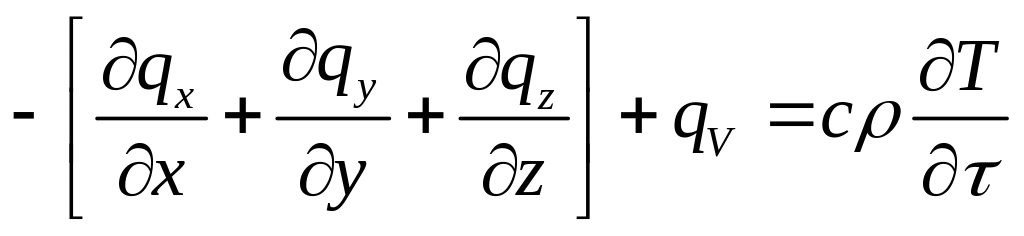(1.13)

 Воспользуемся законом Фурье: , подставив его в уравнение (1.13), получим:

Аналогично подставляем другие члены, в итоге получим:

– уравнение теплопроводности, где (1.14)

В общем случае теплопереноса (с учётом конвективного и диффузионного механизмов переноса тепла) компоненты теплового потока q_x, q_y, q_z, могут быть представлены:

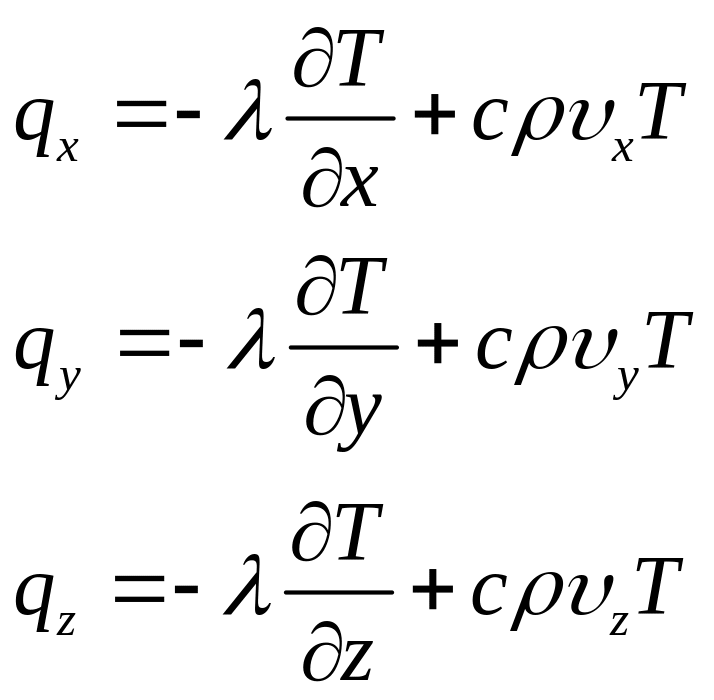(1.15)

Подставив (1.15) в (1.13), получим уравнение энергии:

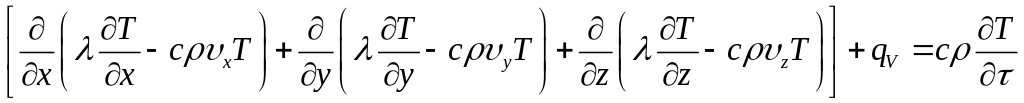
Преобразуем:

Стандартный вид уравнения энергии:

(1.16)

В левой части уравнения (1.16) конвективный теплообмен; T – молекулярный (диффузионный перенос тепла).