Решение алгебраических и трансцендентных уравнений

Часто приходится находить корни уравнений вида , где f(x) определена и непрерывна на некотором интервале.

Если f(x) представляет собой многочлен, то уравнение - алгебраическое, если в функцию входят функции типа: тригонометрических, логарифмических, показательных и т.п., то уравнение называется трансцендентным.

Решение уравнения вида разбивается на два этапа:

1. отделение корней, т.е. отыскание достаточно малых областей, в каждой из которых заключен один и только один корень уравнения;

2. вычисление выделенного корня с заданной точностью.

Первый этап более сложный, в этом случае может помочь построение приближенного графика функции с анализом на монотонность, смену знака, выпуклость и т.д.

Для вычисления выделенного корня существует множество методов, например:

• метод итераций;

• метод половинного деления;

• метод Ньютона.

x-2+sin(1/x)=0

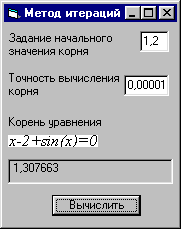
Метод итераций

Уравнение можно представить в виде: .

Например: x-2+sin(1/x)=0 → x=2-sin(1/x)

Далее на отрезке [a,b], где функция имеет корень, выбирается произвольная точка x₀ и далее последовательно вычисляется:

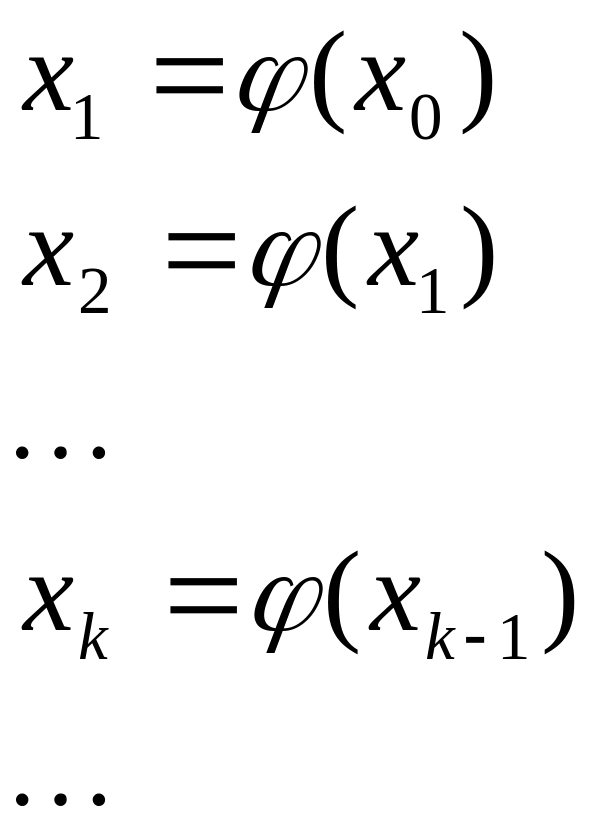Процесс вычисления значений x_k называется итерационным процессом.

Если на отрезке [a,b] выполнено условие |φ΄(x)| ≤ q <1, то итерационный процесс сходится к корню уравнения .

Если необходимо вычислить корень с точностью ε, то процесс итераций продолжается до тех пор, пока для двух последовательных приближений x_n и x_n-1 не будет выполнено:

, при этом всегда выполняется , где ε заданная абсолютная погрешностью корня x*.

Если q ≤0.5 , то можно пользоваться соотношением .

В приведенном примере |φ΄(x)|= |(2-sin(1/x))΄|=cos(1/x)/x^2 < 0,47 на отрезке [1.2,2]

VB

Метод половинного деления

Функция непрерывна на отрезке [a,b] и имеет на его концах разные знаки. Известно, что на отрезке [a,b] функция имеет только один нуль, т.е. корень уравнения один.

Отрезок [a,b] делится пополам x1=(a+b)/2, если , это корень уравнения. Если нет, то выбираем тот из отрезков [a,x1] или [x1,b], на концах которого функция имеет разный знак. Полученный отрезок снова делится пополам, и проводятся те же рассуждения. Продолжаем до тех пор, пока длина отрезка не станет меньше заданного ε.

Метод хорд

Идея метода хорд заключается в том, что можно, с известным приближением, допустить, что функция на достаточно малом участке [a,b] изменяется линейно. Тогда кривую y=f(x) на участке [a,b] можно заменить хордой и в качестве приближенного значения корня принять точку пересечения хорды с осью абсцисс.

Угловой коэффициент хорды , тогда уравнение хорды .

Коэффициент m можно определить, например из условия, что при x=a хорда должно выполняться равенство y=f(a). Тогда , откуда , и уравнение хорды принимает вид . Тогда абсцисса точки пересечения хорды с осью Ox (y=0) . Это и есть формула приближенного значения корня, полученного по методу хорд. Иногда удобнее отправится из точки b, тогда формула будет выглядеть так . Эти две формулы тождественны.

Полученное значение x₁ можно использовать для вычисления следующего уточнения корня по методу хорд, рассматривая либо интервал [a,x₁], либо [x₁,b], смотря по тому в каком из них лежит истинный корень (т.е. на концах которого функция меняет знак).

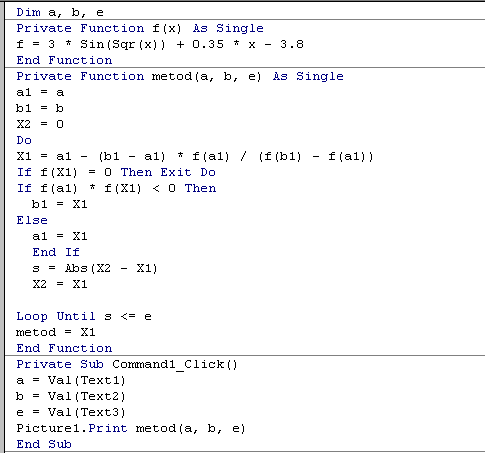
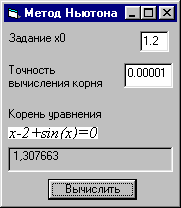
Метод Ньютона (касательных)

Функция , причем f΄(x) и f˝(x) определены, непрерывны и сохраняют постоянные знаки на отрезке [a,b].

Например как функция:

f(x) =x-2+sin(1/x) f΄(x)=1-cos(1/x)/x^2 f˝(x)=-(sin(1/x)-2*x*cos(1/x))/x^4

на отрезке [1.2,2]

Выбирается некоторая точка x₀ на отрезке [a,b] таким образом, что значение функции и ее второй производной имеют одинаковый знак, и строится касательная к графику функции в точке [x₀,f(x₀)]. Уравнение касательной имеет вид

y-f(x₀)=f′(x₀)*(x-x₀).

Точка пересечения касательной с осью абсцисс (y=0) , далее ищется точка пересечения с осью абсцисс касательной построенной к графику функции в точке [x₁,f(x₁)] и т.д., т.е. последовательно вычисляются:

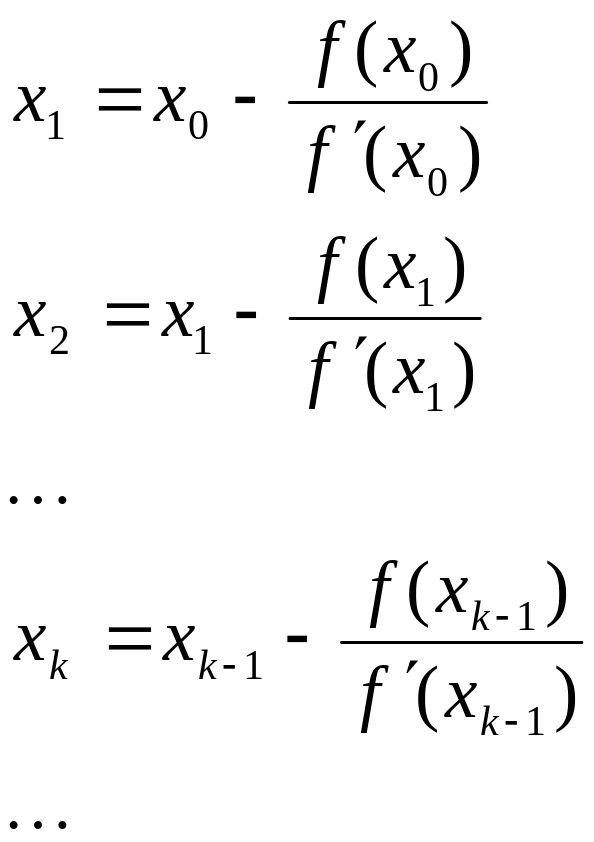Процесс последовательных приближений по методу Ньютона.

Если начальное приближение x₀ выбрано таким образом, что f(x₀)*f˝(x₀) >0, то сходимость метода Ньютона обеспечена (т.е. сходимость x₁, x₂, …, x_n к корню уравнения).

Если корень вычисляется с точностью до ε , то процесс вычислений следует прекратить, когда

,

где m1 - наименьшее значение |f΄(x)| и на [a,b],

M2 - наибольшее значение |f˝(x)| на [a,b].

При этом выполняется , где ε – заданная предельная абсолютная погрешность корня x^*.

Если , то верно

Вычисление определенных интегралов

Функция задана аналитически.

Отрезок интегрирования разбивается на n равных частей длины

Точки разбиения: x₀=a x₁=x₀+h … x_i=x₀+ih… x_n=b.

Функция вычисляется в точках разбиения y_i=f(x_i).

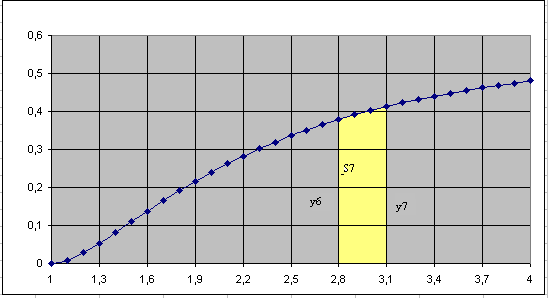
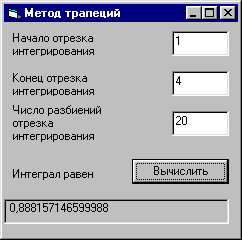
Метод трапеций (для аналитически заданной функции)

Тогда согласно методу трапеций

Например, вычислить интеграл Площадь трапеции:

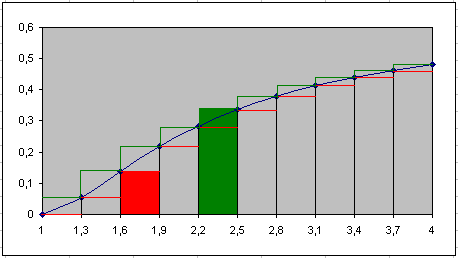
Метод прямоугольников

Например, вычислить интеграл Площадь прямоугольника: ∆S1=y1* h

левые концы участков, (1)

правые концы участков. (2)

Погрешность формулы прямоугольников можно получить, рассматривая разность результатов, полученных по формулам (1) и (2).

Метод Симпсона

Отрезок интегрирования разбивается на четное число 2n равных частей длины h=(b-a)/2n.

a=x₀ < x₁ < …< x_2n-1 < x_2n = b

Рассматривается пара соседних участков и через три точки кривой с координатами (x₀,y₀), (x₁,y₁), (x₂,y₂) проводится парабола с осью, параллельной оси Oy.

Ее уравнение y=Ax² +Bx +C. Площадь криволинейной трапеции на участке [x₀,x₂] заменяется площадью криволинейной трапеции, ограниченной параболой.

Если вынести за скобку общий множитель x₂-x₀ и привести к общему знаменателю, получится

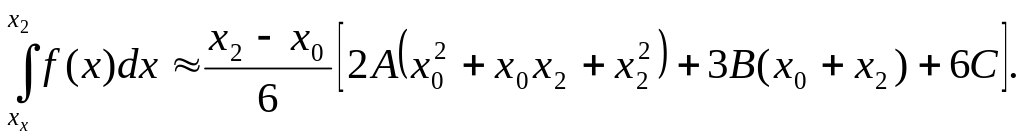(0)

Неизвестные коэффициенты A, B, C находятся из условия, что при значениях x равных x₀, x₁,x₂, функция f(x) принимает соответственно значения y₀, y₁, y₂. Если взять , то условия можно записать

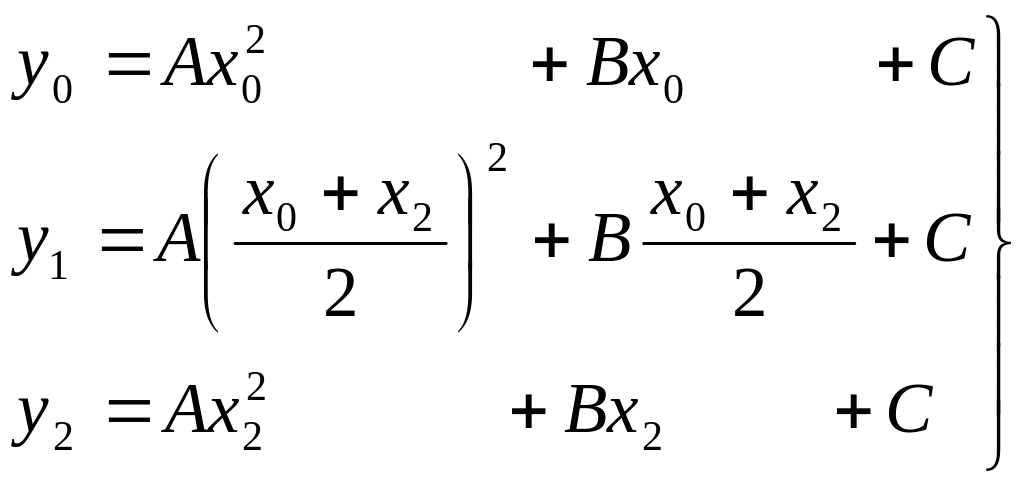(0)

Второе равенство умножается на четыре, все три равенства складываются, получается

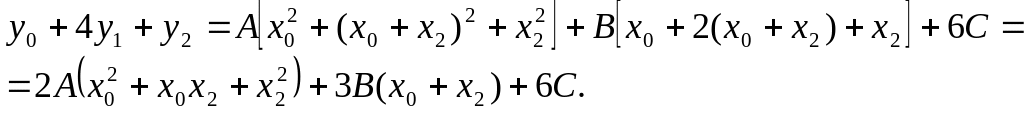(0)

Что совпадает с квадратной скобкой в правой части равенства (1). Если подставить (3) в (1), и заметить, что x₂ –x₁=2h, (h=(b-a)/(2n)), то получится

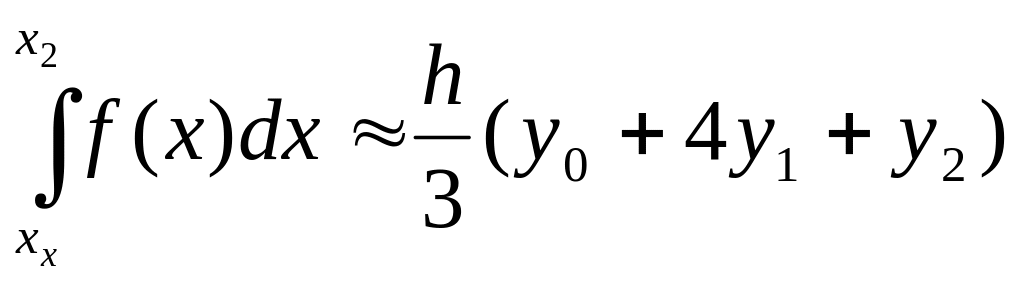(0)

Для каждой следующей пары участков получится такая же формула

(0)

Суммируя равенства вида (4) и (5) по всем участкам можно получить

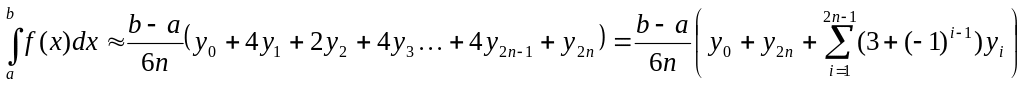
или, если обозначить N=2n

.

Это и есть формула Симпсона. Ее называют также формулой парабол.

Переменная с=1 для нечетных i и –1 для четных, т.о. реализуется коэффициент (-1)i-1.

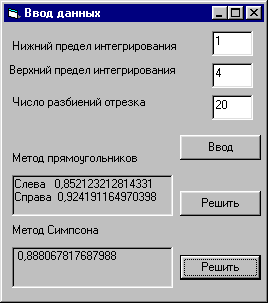
Результаты вычисления интеграла , полученные разными методами:

Метод		Результат
MatLab	трапеций Симпсона Лобатто	0.88815714659999 0.88807223886900 0.88806573865982
MathCad		0.88806573863715
Трапеций		0.88815714659998
Прямоугольников	слева справа среднее	0.852123212814331 0.924191164970398 0.8881571888923645
Симпсона		0.888067817687988