Лекция 1

Линейная алгебра и аналитическая геометрия

Матрицы и действия над ними

Опр.: Матрица – прямоугольная таблица чисел, состоящая их m строк и n столбцов.

Матрицу, имеющую m строк и n столбцов, называют матрицей размером .

Матрица из одной строки называется строчная матрица или матрицей строкой.

Матрица из одного столбца называется матрицей столбцом.

Матрица, все элементы которой равны нулю, называется нулевой матрицей.

Матрица называется квадратной, если число строк равно числу столбцов, т.е. m=n.

Квадратная матрица называется симметрической, если . Элементы a₁₁, a₂₂, …, a_nn образуют главную диагональ квадратной матрицы.

Диагональной матрицей называется квадратная матрица, у которой все элементы которой, не принадлежащие главной диагонали, равны нулю.

Единичной матрицей называется диагональная матрица, у которой все элементы главной диагонали которой = 1

Действия над матрицами:

Линейными операциями над матрицами называется сложение, вычитание, умножение матрицы на число. Сложение, вычитание матриц определено только для матриц одинаковой размерности.

1. Равенство матриц:

Две матрицы равны, если равны их соответствующие элементы.

2. Умножение матрицы на число:

3. Сложение, вычитание матриц: A и B –матрицы,

Линейные операции над матрицами обладают свойствами:

1. A+B=B+A

2. (A+B)+C=A+(B+C)

3. A+(-A)=0

4. A·1=A

5. A+0=A

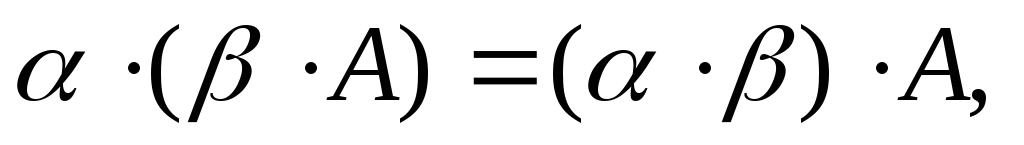6. где ,– действительные числа

7. α∙(A+B)= α Α+ α B, где α - действительное число

8. (α+)A=αA+A, где α, - действительные числа

4. Умножение матриц определено только для согласованных матриц.

Опр.: Матрица A называется согласованной с матрицей B, если число столбцов матрицы A равно числу строк матрицы B, следовательно, из согласованности матрицы A с B не следует согласованность матрицы B с A.

Если матрицы А и В квадратные, то они взаимно согласованы.

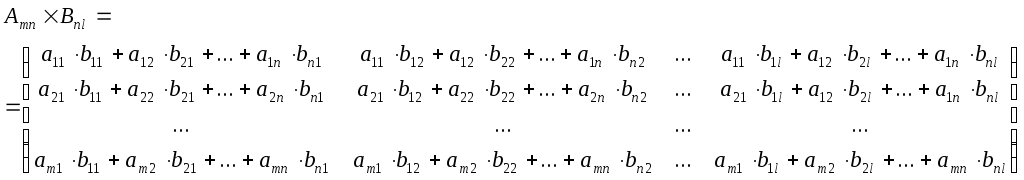
Пример:

Если для матриц А и В определены произведения А∙B и В∙А, то А∙B не всегда равно В∙А.

Если А∙B= В∙А, то матрицы перестановочные, например:

А∙Е=Е∙А=А

А∙0=0∙А=0

Свойства:

1. (А∙В)∙С=А∙(В∙С)

2. α∙(А∙В)=(α∙А)∙В=А∙(α∙В)

3. (А+В)∙С=А∙С+С∙В

4. С(А+В)=СА+CВ

5. А и В – квадратные, тогда det(A∙B)= detA∙ detB

Определители 2,3 порядка

Опр.: Определителем квадратной матрицы 2 порядка называется число, равное:

Det A=▲= а_11*а₂₂-а_12*а_{21 =} .

Опр.: Определителем 3 порядка называют число, равное:

Det A= =a₁₁ ∙ a₂₂ ∙ a₃₃ + a₂₁ ∙ a₃₂ ∙ a₁₃ + a₁₂ ∙ a₂₃ ∙ a₃₁ – a₁₂ ∙ a₂₂ ∙ a₃₁ – a₁₁ ∙ a₃₂ ∙ a₂₃–a₁₂ ∙ a₂₁ ∙ a_33.

Опр.: Минором элемента определителя a_ij называют определитель, полученный из данного вычеркиванием той строки или того столбца, на которой находится данный элемент. Обозначение - (M_ij).

Опр.: Алгебраическим дополнением элемента a_ij называется его минор, взятый со знаком (-1)^i+j

A_ij= (-1) ^i+j∙M_ij.

Свойства:

1. Определитель не изменяется при замене всех его строк соответствующими столбцами (транспонирование).

=

2. При перестановке 2 столбцов или строк определитель меняет знак.

=-

3. Определитель с двумя одинаковыми столбцами или строками равен нулю.

Det A= = 0

Если определитель будет иметь 2 одинаковых строки или столбца, то, переставив их местами, получим то же, но по сойству 2 при этом определитель меняет знак => Det A = (-DetA) => det A =0.

4. Множитель общий для элементов некоторой строки или столбца можно вынести за знак определителя.

5. Определитель, содержащий нулевую строку или столбец, равен нулю.

6. Если в определителе есть сумма, то определитель равен сумме двух определителей:

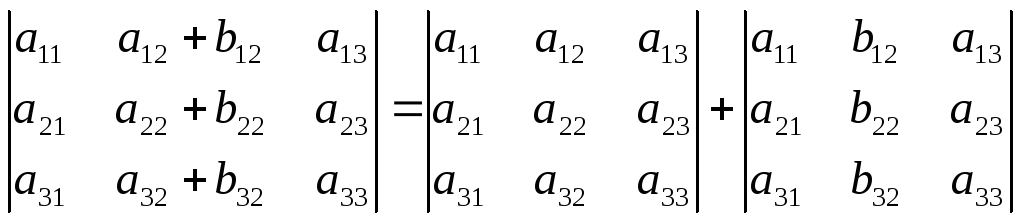
7. Величина определителя не изменится, если элементам любого столбца или строки прибавить элементы другого столбца или строки, предварительно умноженные на какое-либо число.

Лекция 2

Th: Теорема о разложении определителя по элементам строки или столбца

Определитель равен сумме произведений какой-либо строки или столбца на их алгебраические дополнения.

Аналогично доказывается разложение определения по другим строкам или столбцам.

Пример:

Замечание: Сумма произведения элементов строки или столбца на алгебраические дополнения другой строки или столбца равна 0.

Определители n-го порядка.

Рассмотрим n элементов. Число всевозможных перестановок равно n-факториал.

Опр. Если в перестановке элемент с большим номером стоит раньше чем элемент с меньшим номером, то эти элементы образуют инверсию.

Пример: рассмотрим перестановку (2,1, 4, 3, 7, 6, 5)

Число инверсий – (2,1, 4, 3, 7, 6, 5) = 2 инв.+1 инв.+0 инв. + 1 инв. +0 инв. + 1 инв. = 5 инверсий.

Определение: Перестановка, содержащая нечетное количество инверсий, называется нечетной. Перестановка, содержащая четное количество инверсий, называется четной.

Определение: Определителем n-го порядка называется число, обозначаемое символом , и равное сумме всех n! произведений элементов, взятых по одному из каждого столбца и каждой строки, т.е. , взятых со знаком +, если перестановка i,j,r – четная и со знаком -, если перестановка - нечетная.

Для определителя 2-го порядка:

- перестановка четная (1, 2) – (+)

- перестановка нечетная (2,1) - (-)

Но на практике обычно определители высоких порядков обычно вычисляют по теореме о разложении определителя по элементам строки или столбца, т.е справедлива формула - формула разложения определителя по i-той строке.

Обратная матрица.

Дана квадратная матрица

Опр.: Квадратная матрица называется неособенной, если определитель этой матрицы не равен нулю, в противном случае матрица называется особенной.

Матрица A^-1 называется обратной матрице А, если А^-1*А=А*А^-1=Е.

Th: Для того, чтобы квадратная матрица А имела обратную матрицу, необходимо и достаточно, чтобы определитель этой матрицы был не равен нулю.

Доказательство:

(необходимость).

Дано: матрица А имеет обратную матрицу А^-1.

Доказать: detA0.

Так как матрица А имеет А^-1

А^-1*А=А*А^-1=Е (по опр.)

Рассмотрим правую часть А*А^-1=Е

Det A *detA^-1=det E (по свойству 5 умножения матриц)

Но det E =1 =>

det A *det A^-1=10detA0.

(достаточность).

Дано: detA0.

Доказать: А^-1- существует.

Рассмотрим вспомогательную матрицу С, которая составлена следующим образом: элементы матрицы А транспонируются (строки заменяются столбцами) и для всех элементов транспонированной матрицы А находим алгебраические дополнения, которое и составляют С.

(по теореме о разложении определителя по элементам строки или столбца)

И так как по условию

или (*), (по свойствам умножения матриц на число)

Аналогично находим, что

C*A=det A*E

(**)

(*), (**), но

А^-1*А=А*А^-1=Е, следовательно

- формула для нахождения обратной матрицы.

Пример:

^,

Система n линейных уравнений с n неизвестными.

Общий вид:

Введем в рассмотрение определитель, состоящий из коэффициентов при неизвестных:

Опр.: Решением системы является совокупное значение неизвестных (x₁=c₁,x₂=c₂.., x_n=c_n), которые при подстановке в систему обращают каждое уравнение в тождество.

Опр.: Система, имеющая решение называется совместной, в противном случае несовместной.

Опр.: Совместная система, имеющая одно решение, называется определённой; множество решений - неопределенной.

Th: Теорема Крамера:

Если определитель системы линейных уравнений отличен от нуля, то система имеет единственное решение, и находятся по формулам.

Умножим первое уравнение системы линейных уравнений на алгебраическое дополнение А₁₁, второе – на А₂₁, и так далее – последнее – на А_n1, сложим, и сгруппируем по неизвестным:

Введем в рассмотрение определитель:

= (по теореме о разложении определителя)=

Получаем, что , где - определитель, полученный из определителя системы заменой первого столбца столбцом свободных членов. Остальные формулы получаются аналогично, умножая СЛУ на и т.д.:

(*)

И т.к. по условию , то

- формулы Крамера.

Рассмотрим соотношение (*):

1. Если , то , т.е. система имеет множество решений.

2. Если 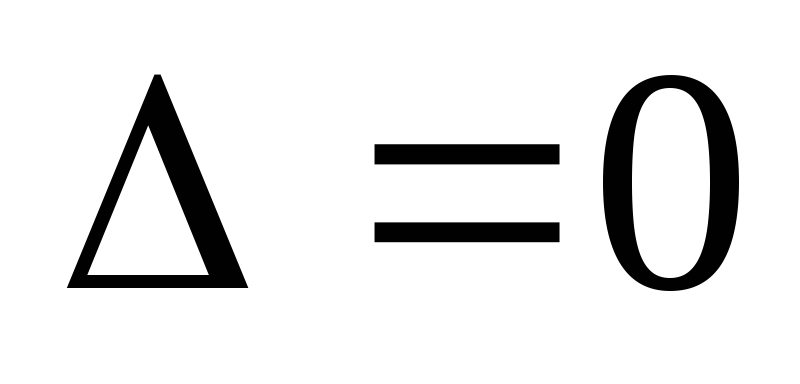, но хотя бы один из определителей отличен от нуля, то система не имеет решений (на 0 делить нельзя).

Однородная система линейных уравнений:

Общий вид:

Здесь всегда .

1. Если , то система имеет единственное решение

2. Если , то СЛУ имеет множество решений.

Лекция 3

Матричный способ решения систем из n уравнений с n неизвестными.

Общий вид:

, , А=, тогда заданная система запишется в виде:

A*Х=B. Предположим, что матрица А – неособенная.

Det A0существует А^-1. Равенство А*Х=В умножим слева на обратную матрицу А^-1.

А^-1*А*Х=A^-1*B

E*Х= A^-1*B

X=A^-1*B – формула для нахождения неизвестной матрицы Х.

Пример:

Ранг матрицы.

Рассмотрим произвольную матрицу, содержащую m строк и n столбцов.

Опр.: Выделим в матрице А k строк и k столбцов; элементы матрицы, стоящие на пересечении выделенных строк и столбцов, являются элементами определителя k–го порядка, который называется минором матрицы k–го порядка.

Пример:

=***

М₁-любой элемент матрицы.

М₄=0, так как есть 3 строки, а 4 строка – нулевая.

Среди всех миноров матриц различных порядков есть миноры, равные нулю, есть миноры, отличные от нуля.

Опр.: Наивысший порядок отличного от нуля минора, называется рангом матрицы [r(A)].

Пр.:

Из определения ранга матрицы следует утверждение:

1. 0 ≤ r ≤ min(m,n)

2. r = 0, тогда и только тогда, когда матрица нулевая

3. для квадратной матрицы порядка n, r=n, тогда и только тогда, когда матрица не особенная.

Элементарные преобразования матриц:

1. Транспонирование – строки меняются местами со столбцами;

2. Перестановка двух строк или столбцов;

3. Умножение элементов некоторой строки или столбца на λ, где λ≠0;

4. Прибавление к элементам какой-либо строки или столбца элементы другой строки или столбца, предварительно умноженные на некоторое число.

Th: Элементарные преобразования ранга матрицы не меняют.

Так как ранг – наивысший порядок отличного от нуля минора (т.е. является определителем), то по свойствам определителей преобразование 1. величины определителя, а соответственно и минора, не меняет.

Преобразование 2. меняет знак минора на противоположный.

Преобразование 3. увеличивает величину минора в λ-раз

Преобразование 4. величину минора (определителя) не меняет.

Следовательно, в результате перечисленных преобразований, миноры неравные нулю, останутся неравными нулю, а миноры, равные нулю, остаются равными нулю. Это означает, что ранг матрицы не меняется.

Пример: