
- •Определители n-го порядка.
- •Обратная матрица.
- •Система n линейных уравнений с n неизвестными.
- •Произвольная система линейных уравнений.
- •Линейные операции над векторами в координатной форме.
- •Линейное пространство
- •Размерность и базис линейного пространства
- •Скалярное произведение векторов
- •Скалярное произведение в координатной форме
- •Векторное произведение векторов.
- •Векторное произведение в координатной форме
- •Смешанное произведение векторов.
- •Аналитическая геометрия Простейшие задачи аналитической геометрии
- •Полярная система координат
- •Формулы преобразования системы координат
- •1. Параллельный перенос
- •Поворот осей координат
- •Уравнение прямой на плоскости
- •Нормальное уравнение прямой
- •Расстояние от точки до прямой
- •Нормальное уравнение прямой
- •Расстояние от точки до плоскости
- •Угол между двумя прямыми в пространстве
- •Асимптоты гиперболы
- •Эксцентриситет гиперболы, фокальные радиусы гиперболы
- •Парабола
- •Общие свойства кривых второго порядка
- •Приведение общего уравнения второго порядка к каноническому виду
Расстояние от точки до прямой
Дано: прямая l
задана нормальным уравнением в векторной
форме
![]()
![]()
![]()
![]() Требуется найти расстояние от точки до
прямой.
Требуется найти расстояние от точки до
прямой.
Возможны 2 случая:
-
т. М0 и начало координат лежат по разные стороны от прямой
-
т. М0 и начало координат лежат по одну сторону от прямой
Рассмотрим 1 случай.
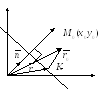 соединим
соединим
![]() и 0
и 0
![]() - радиус вектор точки М0
- радиус вектор точки М0
Опустим из точки
![]() перпендикуляр на l,
обозначим точкой K(x,y)
перпендикуляр на l,
обозначим точкой K(x,y)
![]() - расстояние от
точки до прямой. Соединим точку О
с точкой K,
получим
- расстояние от
точки до прямой. Соединим точку О
с точкой K,
получим
![]() - радиус-вектор точки К.
- радиус-вектор точки К.
Из треугольника ОМ0К видно, что
![]() с одной стороны,
а с другой стороны
с одной стороны,
а с другой стороны
![]()
![]() ,
а так как точка К принадлежит l,
значит, координаты ее радиус вектора
координаты удовлетворяют уравнению
,
а так как точка К принадлежит l,
значит, координаты ее радиус вектора
координаты удовлетворяют уравнению
![]() подставляем и получаем
подставляем и получаем
![]() по свойству скалярного произведения
по свойству скалярного произведения
![]() ,
отсюда
,
отсюда
![]() - расстояние от точки до прямой
- расстояние от точки до прямой
Во втором случае
![]()
![]()
![]()
![]()
![]()
![]() - общий случай
- общий случай
![]()
![]()
![]() - расстояние от
точки до прямой в координатной форме.
- расстояние от
точки до прямой в координатной форме.
![]() - отклонение
точки от прямой
- отклонение
точки от прямой
Если Δ>0, то
![]() и 0 лежат по разные стороны от прямой
и 0 лежат по разные стороны от прямой
Если Δ<0, то по одну сторону от прямой
Вывод.: чтобы найти расстояние от точки до прямой, нужно уравнение привести к нормальному виду и подставить вместо х и у координаты заданной точки.
Пр.:
![]() 12х+15у+9=0
12х+15у+9=0
![]()
![]()
![]()
![]()
![]()
Каноническое уравнение прямой.
Параметрическое уравнение прямой.
Дано: прямая l,
такая что
![]() ,
,
![]()
![]() ,
,
![]() - направляющий вектор прямой l,
возьмем произвольную точку M
на прямой l
и рассмотрим
- направляющий вектор прямой l,
возьмем произвольную точку M
на прямой l
и рассмотрим
![]()
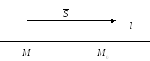 ,так
как
,так
как
![]() ,то
,то
![]() и коллинеарные, следовательно их
коэффициенты пропорциональны.
и коллинеарные, следовательно их
коэффициенты пропорциональны.
![]() - каноническое
уравнение прямой
- каноническое
уравнение прямой
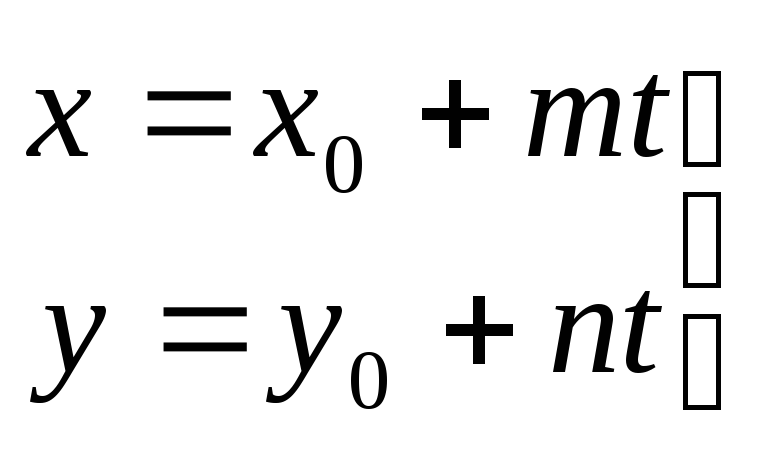 - параметрическое
уравнение прямой, t
– параметр.
- параметрическое
уравнение прямой, t
– параметр.
Уравнение прямой проходящей через две заданные точки
Дано: прямая l,
![]() и
и
![]()
 Возьмем
точку
Возьмем
точку
![]() и рассмотрим два вектора
и рассмотрим два вектора
![]() и
и
![]() - эти вектора коллинеарны, следовательно
коэффициенты пропорциональны
- эти вектора коллинеарны, следовательно
коэффициенты пропорциональны
![]() - уравнение прямой
проходящей через две заданные точки
- уравнение прямой
проходящей через две заданные точки
Уравнение прямой с угловым коэффициентом

![]() - угловой коэффициент
- угловой коэффициент
![]()
![]()
![]() -уравнение
прямой с угловым коэффициентом
-уравнение
прямой с угловым коэффициентом
Уравнение прямой с угловым коэффициентом, проходящей через заданную точку
Возьмем
![]() (1),
и т.к. точка
(1),
и т.к. точка
![]() ,
то ее координаты удовлетворяют уравнению
прямой:
,
то ее координаты удовлетворяют уравнению
прямой:
![]() (2),
из (2) вычтем (1), получаем:
(2),
из (2) вычтем (1), получаем:
![]() - уравнение прямой, проходящей через
заданную точку.
- уравнение прямой, проходящей через
заданную точку.
Угол между двумя прямыми

![]() и
и
![]() - угловой коэффициент
- угловой коэффициент
![]()
![]()
так как
![]() - внешний угол, то
- внешний угол, то

Условие параллельности двух прямых
![]() =0
=0
![]()
![]() -условие
параллельности прямых
-условие
параллельности прямых
Условие перпендикулярности двух прямых
![]()
![]()
![]()
![]() - условие
перпендикулярности двух прямых
- условие
перпендикулярности двух прямых
Уравнение пучка прямых
Дано: две
пересекающиеся прямые 1:![]() ,
пусть т. М0
(x0,
y0)
точка пересечения, тогда
,
пусть т. М0
(x0,
y0)
точка пересечения, тогда
![]() (*)
(*)
Первое уравнение
умножим на
![]() ,
второе – на
,
второе – на
![]() и сложим:
и сложим:
![]() - это уравнение
определяет прямую Покажем, что она
проходит через точку
М0
(x0,
y0):
- это уравнение
определяет прямую Покажем, что она
проходит через точку
М0
(x0,
y0):
![]() - см. (*).
- см. (*).
Таким образом,
![]() - уравнение пучка прямых.
- уравнение пучка прямых.
Разделим обе части
на
![]() :
:
![]()
![]()
уравнение пучка
прямых -
![]()
Уравнение плоскости в пространстве
Уравнение плоскости, проходящей через данную точку и имеющей нормальный вектор
Дано: плоскость
Р,![]()
Н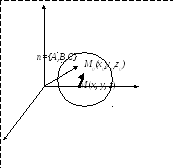 аписать
уравнение прямой.
аписать
уравнение прямой.
Возьмём точку
![]() произвольная точка и рассмотрим вектор
произвольная точка и рассмотрим вектор
![]()
![]()
![]()
![]() ;
раскроем скобки
;
раскроем скобки
![]() - уравнение
плоскости, проходящей через данную
точку и имеющей нормальный вектор.
Раскроем скобки:
- уравнение
плоскости, проходящей через данную
точку и имеющей нормальный вектор.
Раскроем скобки:
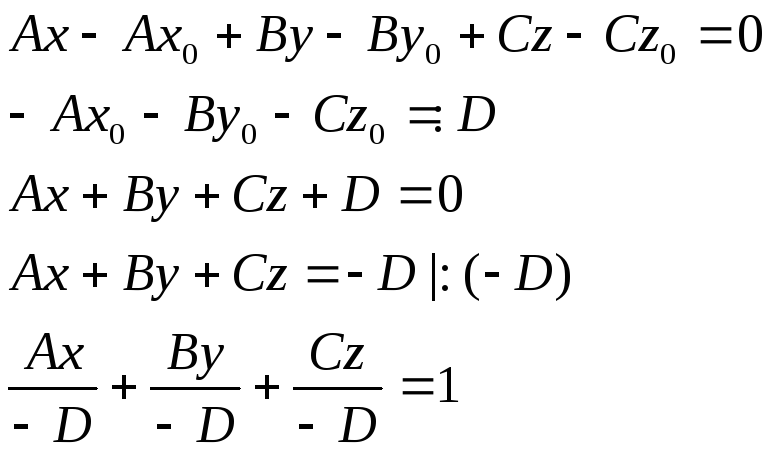 -
общее уравнение плоскости
-
общее уравнение плоскости
![]()
![]() - уравнение плоскости
в отрезках
- уравнение плоскости
в отрезках
Неполные уравнения плоскости
![]() - дано общее
уравнение плоскости;
- дано общее
уравнение плоскости;
1.
![]() представляет
собой плоскость, проходящую через начало
координат;
представляет
собой плоскость, проходящую через начало
координат;
2.
![]() - представляет
собой плоскость, параллельную оси ОZ,
так как вектор
- представляет
собой плоскость, параллельную оси ОZ,
так как вектор
![]()
Аналогично, если В=0, то плоскость параллельна ОУ, если А=0, то плоскость параллельна ОХ.
3.
![]() - с одной стороны,
плоскость параллельна ОХ,
так. как А=0,
с другой стороны плоскость проходит
через начало координат, следовательно,
плоскость проходит через ось ОХ;
- с одной стороны,
плоскость параллельна ОХ,
так. как А=0,
с другой стороны плоскость проходит
через начало координат, следовательно,
плоскость проходит через ось ОХ;
Аналогично, если
B=0, D=0,
то плоскость
![]() проходить через
ось ОУ;
проходить через
ось ОУ;
если C=0,
D=0, то плоскость
![]() проходит через
ось ОZ.
проходит через
ось ОZ.
4. Если B=0,
C=0,
то плоскость
![]() параллельна как
оси ОУ,
так оси OZ,
следовательно, она параллельна
координатной плоскости YOZ;
параллельна как
оси ОУ,
так оси OZ,
следовательно, она параллельна
координатной плоскости YOZ;
Аналогично, если
A=0,B=0,
то
![]() параллельна плоскости XOY;
параллельна плоскости XOY;
если A=0,
C=0,
то плоскость
![]() параллельна плоскости XOZ.
параллельна плоскости XOZ.
5. A=0,B=0, D=0, следовательно Z=0 – плоскость XOY;
B=0,C=0, D=0,следовательно X=0 – плоскость YOZ;
A=0, C=0, D=0, следовательно Y=0 – плоскость XOZ.
