ТЮМЕНСКАЯ ГОСУДАРСТВЕННАЯ

СЕЛЬСКОХОЗЯЙСТВЕННАЯ АКАДЕМИЯ

ЛАБОРАТОРНЫЙ ПРАКТИКУМ

ПО

МАТЕМАТИЧЕСКОЙ

СТАТИСТИКЕ

методические указания

и варианты индивидуальных заданий

для выполнения расчётно-графических

работ

Часть 2

г. Тюмень 2007

Предисловие

В сборнике содержатся методические указания и варианты лабораторной работы по теме: Проверка статистической гипотезы о нормальном законе распределения случайной величины.

Методика сборника обеспечивает самостоятельное выполнение расчётно-графической работы.

Описание лабораторной работы включает краткие теоретические сведения и план выполнения работ; образец выполнения работы; контрольные вопросы; варианты заданий.

Лабораторный практикум содержит 50 вариантов и гарантирует индивидуальность его выполнения.

Рекомендуется для инженерных, экономических и сельскохозяйственных специальностей.

Лабораторная работа № 2 Проверка статистической гипотезы о нормальном законе распределения случайной величины Цель и содержание лабораторной работы №2.

Цель работы: Привить навыки по овладению методом проверки статистической гипотезы о нормальном законе распределения изучаемой случайной величины.

Содержание работы:

1. Проверка гипотезы о нормальном законе распределения с помощью критериев согласия:

• критерия Пирсона

• критерия Романовского

• критерия Ястремского

• критерия Колмогорова

2. Проверка гипотезы о нормальном законе распределения с помощью приближенных методов:

с использованием

с использованием a_{S ,}e_k

графическим методом.

3. Графическая иллюстрация сходства (или расхождения) эмпирического распределения с теоретическим.

Форма отчета:

1. Представление работы по указанному в методике образцу.

2. Самостоятельное изучение теоретического материала с помощью предлагаемых контрольных вопросов.

3. Устное собеседование по работе, сдача зачета.

§ 1.1 Краткие теоретические сведения.

Проверка гипотезы о нормальном законе распределения изучаемой случайной величины относится к задачам первичной обработки эмпирических данных. Она важна как для обоснованного применения методов математической статистики, так и как самостоятельный метод. Зная, что эмпирическое распределение, является нормальным, можно наблюдение заменить расчетом, выявить, плохо обозримые по опытным данным, свойства и тенденции изменения изучаемой случайной величины.

Суть проверки статистической гипотезы о нормальном законе распределения (как, впрочем и любого другого) состоит в сравнении данных о случайной величине, полученных эмпирическим путем и теоретическим, которая производится с помощью некоторой критериальной величины.

Если эмпирическое распределение известно,

то теоретическое:

вычисляется в предположении, что изучаемая случайная величина подчиняется нормальному закону распределения с параметрами , . Если дан интервальный вариационный ряд, то вычисляется по формуле:

В случае дискретного вариационного ряда:

,

Где .

Учитывая, что величина промежутков группировки вариационного ряда, как правило, постоянна и равна h, то

.

Значение находится по таблице с названием “Таблица значений функции

“.

Значение по таблице с названием “Таблица значений функции

“.

Если гипотеза о нормальном законе верна, то расхождение между эмпирическими и теоретическими данными должны расцениваться как случайное, а сходство как неслучайное.

Для характеристики степени расхождения (или сходства) вводят специальную меру, критериальную величину U . Она может быть выбрана различными способами. Например, в качестве U можно взять сумму квадратов отклонений теоретических вероятностей от эмпирических с учетом весовых коэффициентов, или же максимальное отклонение эмпирической функции распределения от теоретической F(х).

Очевидно, что величина U зависит от результатов наблюдений, от их числа и закона распределения, следовательно сама является величиной случайной, подчиняющейся некоторому своему закону распределения. Этот закон, как правило: хорошо изучен, выведена функция плотности распределения, составлены таблицы значений U.

Итак, значение меры U можно найти по формуле на основе эмпирических данных вариационного ряда (U наблюдаемое) и по специальной таблице (U табличное).

Если гипотеза о выбранном законе распределения верна, то значение меры расхождения, вычисленной на основе опытных данных (U набл) не должно превышать возможного ее теоретического значения (U табл). U набл. ≤ U табл.

Или, что тоже самое: если вероятность события P(U набл. ≤ U табл.) - велика, то гипотеза о предполагаемом нормальном законе распределения принимается на определенном уровне значимости , в противном случае гипотеза отвергается, считается, что эмпирические данные плохо согласуются с теоретическими.

Отметим, что факт принятия гипотезы ни в коем случае не может считаться доказательством её справедливости. Он указывает лишь на то, что гипотеза не противоречит опытным данным. Аналогично, факт не принятия гипотезы, не опровергает её, а говорит лишь об её несогласованности с имеющимся набором опытных данных.

Наиболее распространенные критерии согласия:

Критерий согласия Пирсона.

В качестве меры расхождения между теоретическим и эмпирическим распределениями принимается величина «хи-квадрат»:

где - эмпирическая вероятность;

-теоретическая вероятность, соответствующая выбранному закону распределения;

- весовой коэффициент i - той группы; введенный К. Пирсоном;

s – число групп

Или:

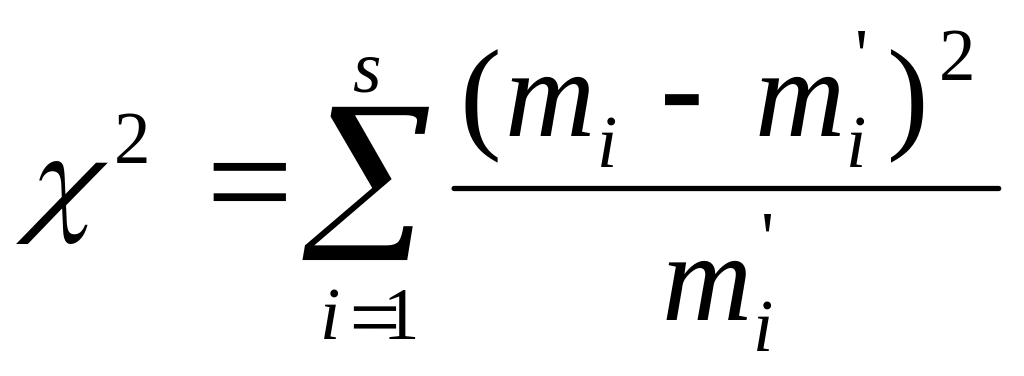
Где -эмпирическая частота; - теоретическая частота.

Согласно закону распределения величины составлена таблица “Критические точки распределения ”, или под названием “Значение в зависимости k, ”

Из таблицы по известным К и p = находят и сравнивают его с , вычисленным по указанной формуле с учетом эмпирических данных.

Если < ( , k), то гипотеза о нормальном законе принимается на уровне значимости , т.е. есть основания считать, что эмпирические и теоретические частоты различаются незначимо, различия случайны. В противном случае гипотеза отвергается на выбранном уровне значимости.

Если по таблице находить не ( , k), а вероятность, с которой принимается значение случайной величины равное при известном числе степеней свободы k, т.е. находить вероятность Р( > ), то вывод о гипотезе зависит от величины этой вероятности.

Если Р, найденное по известным и k значительно отличается от 0, практически больше 0.1, то гипотеза принимается, и отвергается в противном случае.

Для этого способа существует таблица “Значение вероятностей для критерия ”

Критерий согласия Романовского

В качестве меры близости эмпирического и теоретического распределений В.И.Романовский предложил использовать величину , но с учетом числа степеней свободы k,

,

где k - число степеней свободы.

Если величина этого выражения меньше трех , то это дает основание для принятия гипотезы, в противном случае, когда , расхождения считаются существенными и гипотеза о нормальном законе не принимается.

Критерий согласия Ястремского

В качестве меры близости эмпирического и теоретического распределений Б.С. Ястремский предложил использовать величину Х² учетом числа группировок.

где s – количество групп выборки;

Q – величина, зависящая от количества групп, но при числе групп, меньшем 20, она принимается равной 0,6.

Если l <3, то эмпирическое распределение согласуется с теоретическим.

Если l> 3,то эмпирическое распределение не укладывается в теоретическое.

Критерий согласия Колмогорова

В качестве меры расхождения между теоретическим и эмпирическим распределениями А.Н.Колмогоровым предложена величина D - максимальное значение модуля разности между эмпирической функцией распределения и соответствующей теоретической функцией распределения F(x).

D = max |F*(x) - F(x)|

Или, если вместо функций распределения использовать накопленные частоты, то

D = max |M - M'|

где M - накопленная эмпирическая частота;

M' - накопленная теоретическая частота.

В качестве критериальной величины используется ,

где D = max |M - M'|

Величина λ случайная, значения Р (λ) затабулированы.

Таблица имеет название: “Значение функции ”.

По таблице на основе вычисленного λ находят Р(λ).

Если Р(λ) сравнительно велико, практически больше 0.05, то гипотеза принимается. Если Р(λ) мало, практически меньше 0.05, то гипотезу следует отвергнуть, как малоправдоподобную.

Действие критерия основаны на том, что максимальное расхождение (теоретическое) должно быть больше или в крайнем случае равно фактически наблюдаемому, т.е. вероятность должна быть отличной от нуля.

Замечание. Критерий Колмогорова применяется только в том случае, когда параметры предполагаемого закона распределения известны, если они находятся из опытных данных, то критерий дает заведомо завышенное значение Р(λ).

Приближенная проверка

В практике часто используется приближенная проверка на нормальность, в основе которой лежат более простые рекомендации, использующие значения числовых характеристик и свойства нормального закона распределения.

Приближенная проверка с использованием .

Известно, что если случайная величина подчиняется нормальному закону распределения, то её значения удовлетворяют следующим условиям:

промежуток содержит примерно часть всей совокупности значений,

промежуток содержит примерно часть,

промежуток содержит примерно часть,

промежуток содержит примерно 1.

Если эти соотношения выполняются для данной эмпирической совокупности и вычисленных , , то гипотеза о нормальном законе распределения может быть принята.

Приближенная проверка с использованием a_s и е_k

Если эмпирическое распределение подчиняется нормальному закону распределения, то для асимметрии и эксцесса необходимо выполняются следующие условия

,

где - несмещенная оценка для показателя асимметрии,

- несмещенная оценка для показателя эксцесса,

- среднее квадратическое отклонение для показателя асимметрии,

- среднее квадратическое отклонение для показателя эксцесса.

Для использования этой рекомендации необходимо вычислить по эмпирическим данным , , , , , и проверить выполнимость указанных соотношений.

Приближенный графический метод

(метод спрямляемых диаграмм)

Этот метод основан на понятии р - квантили.

Определение. р - квантилью (квантилем) случайной величины называется такое значение аргумента u_p функции распределения F(x), для которого вероятность события X<u_p равна заданному значению р т.е.

Р(Х < u_p) = p

u_p находят по таблице с названием "Квантили нормального распределения u_p" no значениям накопленных эмпирических частот.

Если случайная величина, подчиняется нормальному закону распределения, то точки располагаются вблизи некоторой прямой. (Уравнение прямой т.к. функция распределения общего и нормированного распределений нормального закона связаны c отношением

для данного случая .

Замечание. Если построенные точки оказались вблизи прямой, то можно оценить параметры a и σ. За a можно принять абсциссу точки пересечения прямой с осью OX; За σ разность абсцисс ,где - абсцисса точки прямой с ординатой равной -I (u = -1).

Приближенную проверку на нормальность в реальных условиях целесообразно применять предварительно перед применением более строгих критериев. Полезно также вначале провести качественный анализ изучаемой случайной величины, а именно проанализировать:

1. Является ли она результатом действия большого числа случайных факторов.

2. Независимы ли эти факторы.

3. Имеют ли они примерно одинаково малые воздействия.

Если такие условия, по мнению исследователя, имеют место, то можно ожидать, что изучаемая случайная величина распределена нормально, и имеет смысл проводить более строгое исследование с применением критериев согласия.

Отметим также, что при проверке на нормальность достаточно большим должно быть не только общее число опытов n, но и число наблюдений в отдельных разрядах. На практике рекомендуется иметь в каждом разряде не менее 5-10 наблюдений. Если число наблюдений в отдельных разрядах мало, то имеет смысл объединить некоторые разряды.