
- •Свойства параллельных прямых
- •Признак параллельности прямой и плоскости.
- •1.Параллелепипедом называется призма, основание которой --- параллелограмм.
- •2. Куб или правильный гексаэдр — правильный многогранник, каждая грань которого представляет собой квадрат. Частный случай параллелепипеда и призмы.
Билет 1
Определение. Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.
|
a || b (прямая а параллельна прямой b) прямая с и прямая а не параллельны прямая с и прямая b не параллельны |
рис. 8 |
|
Теорема о параллельных прямых. Через любую точку пространства, не лежащую на данной прямой проходит прямая, параллельная данной, и притом только одна.
|
M |
Свойства параллельных прямых
Свойство 1. Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.
|
|
Свойство 2. Если две прямые параллельны третьей прямой, то они параллельны.
|
|
Определение. Две прямые называются скрещивающимися, если они не лежат в одной плоскости.
Билет 2
Определение. Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.
|
a || b (прямая а параллельна прямой b) прямая с и прямая а не параллельны прямая с и прямая b не параллельны |
рис. 8 |
|
Теорема о параллельных прямых. Через любую точку пространства, не лежащую на данной прямой проходит прямая, параллельная данной, и притом только одна.
|
M a b||а и М b (b - единственная) |
2. Две прямые в трёхмерном евклидовом пространстве скрещиваются, если не существует плоскости, их содержащей. Иначе говоря, две прямые в пространстве, не имеющие общих точек, но не являющиеся параллельными.
Билет 3
2. Угол между двумя прямыми в пространстве
За угол между двумя прямыми в пространстве принимают один из двух смежных углов, который образует прямые, проведенные параллельно данным через какую-нибудь точку в пространстве.
Один из этих углов равен углу между направляющими векторами этих прямых.

Где первая прямая задается:
![]()
а1=( m1, n1, p1)
Вторая прямая задается:

а2=( m2, n2, p2)
Если прямые параллельны, то

Если прямые перпендикулярны, то m1 m2+ n1 n2 + p1 p2=0
Билет 4
1.Определение.
Прямая и плоскость называются
параллельными, если они не имеют общих
точек (а ||
![]() )
)
Признак параллельности прямой и плоскости.
Теорема. Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна самой плоскости.
|
|
Свойства параллельных плоскостей:
|
1. Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны. |
|
2. Отрезки параллельных прямых, заключённые между параллельными плоскостями, равны. |
Билет 5
Теорема 1 ПРИЗНАК ПЕРПЕНДИКУЛЯРНОСТИ ПРЯМОЙ И ПЛОСКОСТИ. Если прямая, пересекающая плоскость, перпендикулярна двум прямым в этой плоскости, проходящим через точку пересечения данной прямой и плоскости, то она перпендикулярна плоскости.

Доказательство:
Пусть
а
прямая, перпендикулярная прямым b
и c
в плоскости
![]() .
Тогда прямая а
проходит через точку А
пересечения прямых b
и c.
Докажем, что прямая а
перпендикулярна плоскости
.
Проведем
произвольную прямую х
через точку А
в плоскости
и
покажем, что она перпендикулярна прямой
а.
Проведем в плоскости
произвольную
прямую, не проходящую через точку А
и пересекающую прямые b,
c
и х.
Пусть точками пересечения будут В,
С
и Х.
Отложим
на прямой а
от точки А
в разные стороны равные отрезки АА1
и АА2.
Треугольник А1СА2
равнобедренный, так как отрезок АС
является высотой по условию теоремы и
медианой по построению (АА1=АА2).
по той же причине треугольник А1ВА2
тоже равнобедренный. Следовательно,
треугольники А1ВС
и А2ВС
равны по трем сторонам.
Из равенства
треугольников А1ВС
и А2ВС
следует равенство углов А1ВХ
и А2ВХ
и, следовательно равенство треугольников
А1ВХ
и А2ВХ
по двум сторонам и углу между ними. Из
равенства сторон А1Х
и А2Х
этих треугольников заключаем, что
треугольник А1ХА2
равнобедренный. Поэтому его медиана ХА
является также высотой. А это и значит,
что прямая х
перпендикулярна а.
По определению прямая а
перпендикулярна плоскости
.
Теорема доказана.
.
Тогда прямая а
проходит через точку А
пересечения прямых b
и c.
Докажем, что прямая а
перпендикулярна плоскости
.
Проведем
произвольную прямую х
через точку А
в плоскости
и
покажем, что она перпендикулярна прямой
а.
Проведем в плоскости
произвольную
прямую, не проходящую через точку А
и пересекающую прямые b,
c
и х.
Пусть точками пересечения будут В,
С
и Х.
Отложим
на прямой а
от точки А
в разные стороны равные отрезки АА1
и АА2.
Треугольник А1СА2
равнобедренный, так как отрезок АС
является высотой по условию теоремы и
медианой по построению (АА1=АА2).
по той же причине треугольник А1ВА2
тоже равнобедренный. Следовательно,
треугольники А1ВС
и А2ВС
равны по трем сторонам.
Из равенства
треугольников А1ВС
и А2ВС
следует равенство углов А1ВХ
и А2ВХ
и, следовательно равенство треугольников
А1ВХ
и А2ВХ
по двум сторонам и углу между ними. Из
равенства сторон А1Х
и А2Х
этих треугольников заключаем, что
треугольник А1ХА2
равнобедренный. Поэтому его медиана ХА
является также высотой. А это и значит,
что прямая х
перпендикулярна а.
По определению прямая а
перпендикулярна плоскости
.
Теорема доказана.
1-ое СВОЙСТВО ПЕРПЕНДИКУЛЯРНЫХ ПРЯМОЙ И ПЛОСКОСТИ. Если плоскость перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой.

Доказательство: Пусть а1 и а2 - 2 параллельные прямые и плоскость, перпендикулярная прямой а1. Докажем, что эта плоскость перпендикулярна и прямой а2. Проведем через точку А2 пересечения прямой а2 с плоскостью произвольную прямую х2 в плоскости . Проведем в плоскости через точку А1 пересечения прямой а1 с прямую х1, параллельную прямой х2. Так как прямая а1 перпендикулярна плоскости , то прямые а1 и x1перпендикулярны. А по теореме 1 параллельные им пересекающиеся прямые а2 и х2 тоже перпендикулярны. Таким образом, прямая а2 перпендикулярна любой прямой х2 в плоскости . А это ( по определению )значит, что прямая а2 перпендикулярна плоскости . Теорема доказана.
Билет6
1.Перпендикуляром, опущенным из данной точки данную плоскость, называется отрезок, соединяющий данную точку с точкой плоскости и лежащий на прямой, перпендикулярной плоскости. Конец этого отрезка, лежащий в плоскости, называется основанием перпендикуляра. Наклонной, проведенной из данной точки к данной плоскости, называется любой отрезок, соединяющий данную точку с точкой плоскости, не являющийся перпендикуляром к плоскости. Конец отрезка, лежащий в плоскости, называется основанием наклонной. Отрезок, соединяющий основания перпендикуляра наклонной, проведенных из одной и той же точки, называется проекцией наклонной.
2.Пусть прямая пересекает плоскость, причем не под прямым, а под каким-то другим углом. Такая прямая называется наклонной.
Опустим перпендикуляр из какой-либо точки наклонной на нашу плоскость. Соединим основание перпендикуляра с точкой пересечения наклонной и плоскости. Мы получили проекцию наклонной на плоскость.

Угол между прямой и плоскостью — это угол между прямой и ее проекцией на данную плоскость.
Обратите внимание — в качестве угла между прямой и плоскостью мы выбираем острый угол.
Если прямая параллельна плоскости, значит, угол между прямой и плоскостью равен нулю.
Если прямая перпендикулярна плоскости, ее проекцией на плоскость окажется точка. Очевидно, в этом случае угол между прямой и плоскостью равен 90°.
Прямая перпендикулярна плоскости, если она перпендикулярна любой прямой, лежащей в этой плоскости.
Это определение. Но как же с ним работать? Как проверить, что данная прямая перпендикулярна всем прямым, лежащим в плоскости? Ведь их там бесконечно много.
На практике применяется признак перпендикулярности прямой и плоскости:
Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в этой плоскости.

Билет 7
1.Перпендикуляром, опущенным из данной точки данную плоскость, называется отрезок, соединяющий данную точку с точкой плоскости и лежащий на прямой, перпендикулярной плоскости. Конец этого отрезка, лежащий в плоскости, называется основанием перпендикуляра. Наклонной, проведенной из данной точки к данной плоскости, называется любой отрезок, соединяющий данную точку с точкой плоскости, не являющийся перпендикуляром к плоскости. Конец отрезка, лежащий в плоскости, называется основанием наклонной. Отрезок, соединяющий основания перпендикуляра наклонной, проведенных из одной и той же точки, называется проекцией наклонной.
2. Теорема 4 О ТРЕХ ПЕРПЕНДИКУЛЯРАХ. Если прямая, проведенная на плоскости через основание наклонной, перпендикулярна ее проекции, то она перпендикулярна наклонной. И обратно: Если прямая на плоскости перпендикулярна наклонной, то она перпендикулярна и проекции наклонной.

Доказательство:
Пусть АВ
- перпендикуляр плоскости
,
АС
- наклонная и с
- прямая в плоскости
,
проходящая через основание С.
Проведем
прямую СA1,
параллельную прямой АВ.
Она перпендикулярна плоскости
.
Проведем через прямые АВ
и СA1
плоскость
![]() .
Прямая с
перпендикулярна прямой СA1.
Если она перпендикулярна прямой СВ,
то она перпендикулярна плоскости
,
а значит, и прямой АС.
АНАЛОГИЧНО.
Если прямая с
перпендикулярна наклонной АС
то она, будучи перпендикулярна и прямой
СA1
перпендикулярна плоскости
,
а значит, и проекции наклонной СВ.
Теорема доказана.
.
Прямая с
перпендикулярна прямой СA1.
Если она перпендикулярна прямой СВ,
то она перпендикулярна плоскости
,
а значит, и прямой АС.
АНАЛОГИЧНО.
Если прямая с
перпендикулярна наклонной АС
то она, будучи перпендикулярна и прямой
СA1
перпендикулярна плоскости
,
а значит, и проекции наклонной СВ.
Теорема доказана.
Билет8
Свойства и признаки
Если плоскость α параллельна каждой из двух пересекающихся прямых, лежащих в другой плоскости β, то эти плоскости параллельны
Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны
Через точку вне данной плоскости можно провести плоскость, параллельную данной, и притом только одну
Отрезки параллельных прямых, ограниченные двумя параллельными плоскостями, равны
Два угла с соответственно параллельными и одинаково направленными сторонами равны и лежат в параллельных плоскостях
Билет 9
Теорема 5 ПРИЗНАК ПЕРПЕНДИКУЛЯРНОСТИ ПЛОСКОСТЕЙ. Если плоскость проходит через прямую перпендикулярную другой плоскости, то эти плоскости перпендикулярны.

Доказательство:
Пусть
-
плоскость , b
- перпендикулярная ей прямая,
-
плоскость проходящая через прямую b,
и с
- прямая по которой пересекаются плоскости
и
.
Докажем, что плоскости
и
перпендикулярны.
Проведем
в плоскости
через
точку пересечения прямой b
с плоскостью
прямую
а,
перпендикулярную прямой с.
Проведем через прямые а
и b
плоскость
![]() .
Она перпендикулярна прямой с,
так как прямые а
и b
перпендикулярны, то плоскости
и
перпендикулярны.
Теорема доказана.
.
Она перпендикулярна прямой с,
так как прямые а
и b
перпендикулярны, то плоскости
и
перпендикулярны.
Теорема доказана.
Билет 10
Билет11
Призма — многогранник, две грани которого являются конгруэнтными (равными) многоугольниками, лежащими в параллельных плоскостях, а остальные грани — параллелограммами, имеющими общие стороны с этими многоугольниками. Или (равносильно) — это многогранник, в основаниях которого лежат равные многоугольники, а боковые грани — параллелограммы.
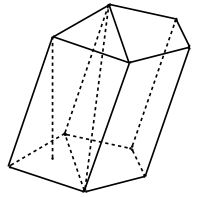
Свойства призмы
Основания призмы равны и лежат в параллельных плоскостях.
Боковые ребра призмы параллельны и равны.
Высота призмы – это любой перпендикуляр, опущенный из любой точки основания на плоскость другого основания.
Боковая поверхность прямой призмы равна произведению периметра основания на высоту призмы, т.е. на длину бокового ребра.
Доказательство
Боковые грани прямой призмы – прямоугольники. Основания этих прямоугольников являются сторонами многоугольника, лежащего в основании призмы, а высоты равны длине боковых ребер. Следовательно, боковая поверхность призмы равна
S = a1l + a2l +…+ anl = pl
где a1, a2, …, an – длины ребер основания, p – периметр основания призмы, а l – длина боковых ребер.
Правильная призма — призма в основании которой лежит правильный многоугольник, а боковые ребра перпендикулярны плоскостям основания.
Основания правильной призмы являются правильными многоугольниками.
Боковые грани правильной призмы являются равными прямоугольниками.
Боковые ребра правильной призмы равны.
Правильная призма является прямой.
Правильная призма, боковые грани которой являются квадратами (высота которой равна стороне основания), является полуправильным многогранником.
Билет 12
Площадь полной поверхности призмы равна сумме площади её боковой поверхности и удвоенной площади основания.
Площадь
боковой поверхности произвольной призмы
![]() ,
где
,
где
![]() —
периметр перпендикулярного сечения,
—
периметр перпендикулярного сечения,
![]() l—
длина бокового ребра.
l—
длина бокового ребра.
Билет13


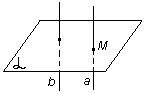 рис.
11
рис.
11 рис.
12
рис.
12 рис.
21
рис.
21
 рис.
26
рис.
26 рис.
26a
рис.
26a