Оператор Гамильтона (набла-оператор).

Для упрощения записи характеристик скалярных и векторных полей был введен символический векторный оператор, имеющий вид 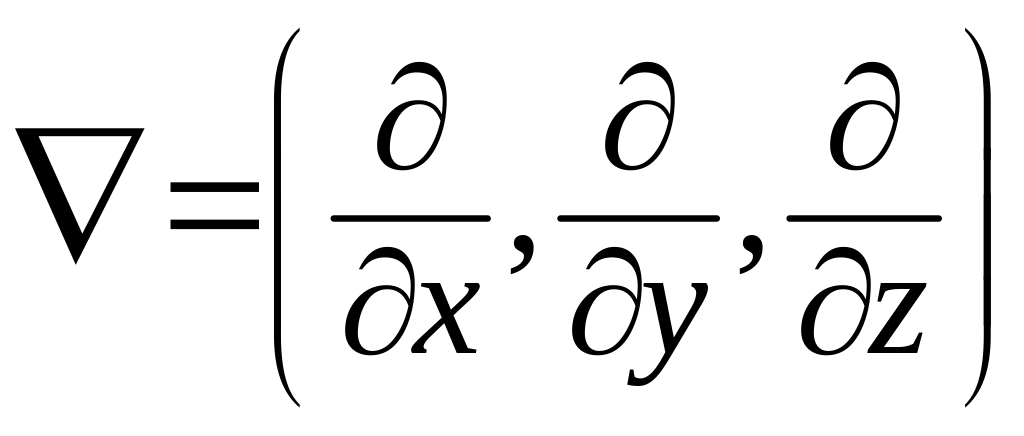. Символическое «умножение» этого оператора на какую-то величину означает, что каждая из компонент оператора применяется к этой величине.

Например, если – скалярная величина, то

.

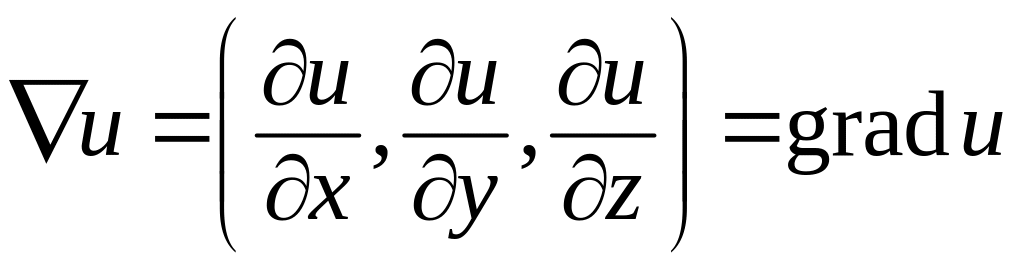Для векторных величин возможно как скалярное, так и векторное умножение. Проследим, что дадут такие произведения с оператором в случае векторного поля .

Скалярное произведение: .

Векторное произведение: .

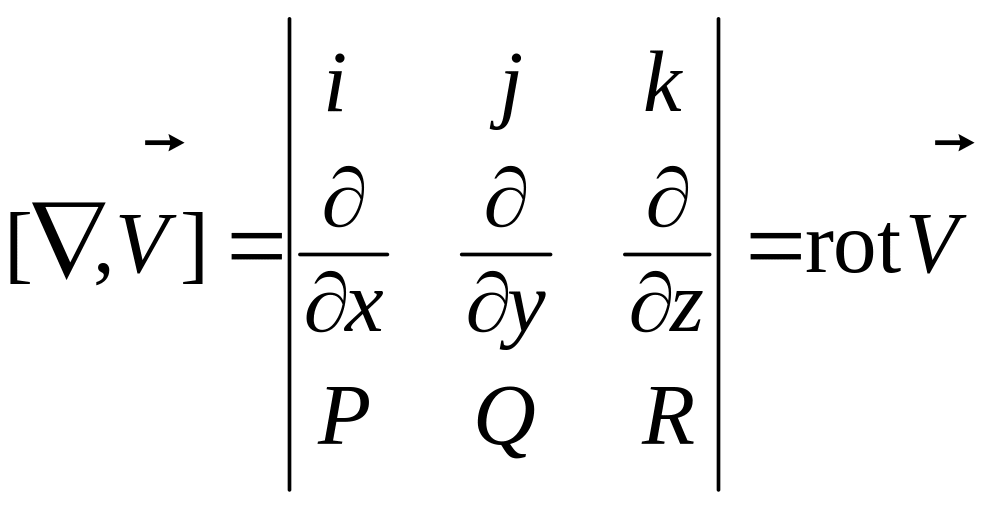Отдельный интерес представляет определенный для скалярных полей оператор

.

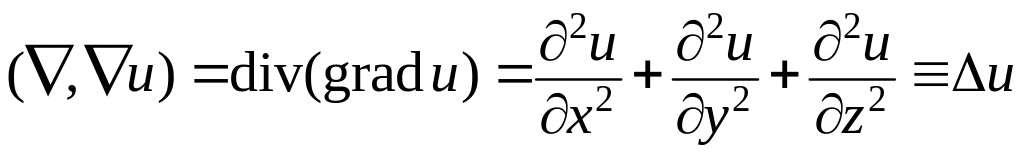Такой оператор называется оператором Лапласа. Функции, удовлетворяющие уравнению Лапласа называются гармоническими в функциями.

Специальные векторные поля.

Потенциальным полем называется поле вектора , , если существует скалярная функция такая, что или . При этом функция называется потенциалом вектора .

Необходимым и достаточным условием того, что поле вектора потенциально, является выполнение равенства

.

Итак, потенциальное векторное поле – это безвихревое, бесциркуляционное поле, так как циркуляция вдоль любого замкнутого контура согласно формуле Стокса равна нулю:

.

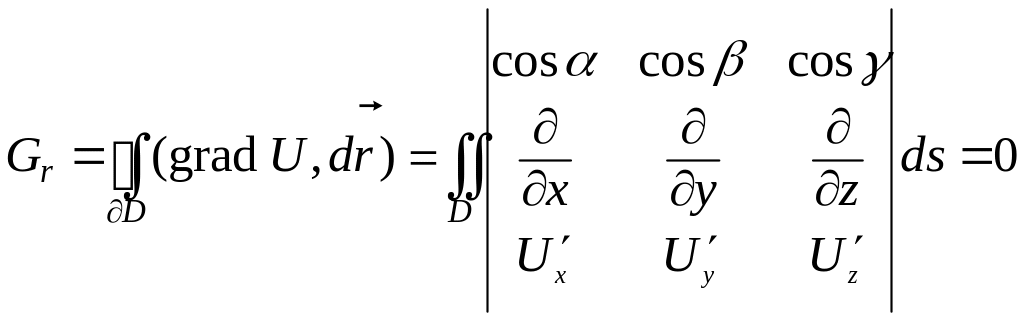Пример потенциального поля – поле ньютоновского притяжения.

Соленоидальным полем называется поле вектора , , если существует вектор-функция , , такая, что или , , . В этом случае вектор-функцию называют векторным потенциалом вектора .

Необходимым и достаточным условием того, что поле вектора соленоидально, является выполнение равенства

.

Необходимое и достаточное условие соленоидальности векторного поля на основе формулы Гаусса-Остроградского обеспечивает равенство нулю потока вектора поля через любую замкнутую и ограничивающую некоторое тело поверхность:

Рассмотрим в «векторную трубку». Так называют поверхность, состоящую из векторных линий, в сечении которой поперечником получается замкнутая кривая.

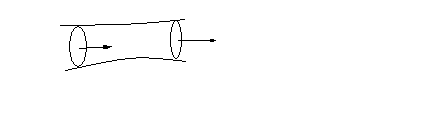
Возьмем замкнутую поверхность, состоящую из векторной трубки и двух поперечников. В соответствии со сказанным выше поток вектора поля через такую замкнутую поверхность равен нулю. Поток через боковую поверхность – векторную трубку – также равен нулю, так как по определению векторных линий направление вектора поля совпадает с направлением векторных линий, и значит, ортогонален к нормали к боковой поверхности. Таким образом, сумма потоков через поперечники внутрь (или вне) замкнутой поверхности равна нулю. Следовательно, в соленоидальном поле поток вектора поля через поперечные сечения векторной трубки сохраняет постоянную величину. Эта величина называется интенсивностью векторной трубки.

Разложение произвольного векторного поля.

Пусть , , – произвольное векторное поле. Покажем, что вектор может быть представлен как сумма двух векторов, один из которых представляет потенциальное, а другой – соленоидальное векторное поле.

Пусть вектор . Какой должна быть эта функция , чтобы вектор был соленоидальным?

Поскольку , получим , то есть . Таким образом, чтобы разложить исходный вектор на сумму потенциального и соленоидального векторов, необходимо сначала решить уравнение Пуассона . Такое уравнение всегда имеет решение (и даже бесчисленное множество решений). Определив , мы получим потенциальный вектор . Теперь по построению вектор соленоидальный. Следовательно, требуемое разложение построено.