Замена переменных в двойном интеграле.

Если переменные в двойном интеграле являются функциями переменных то двойной интеграл от функции по области равен интегралу по области от функции , умноженной на модуль якобиана . То есть, справедлива формула

.

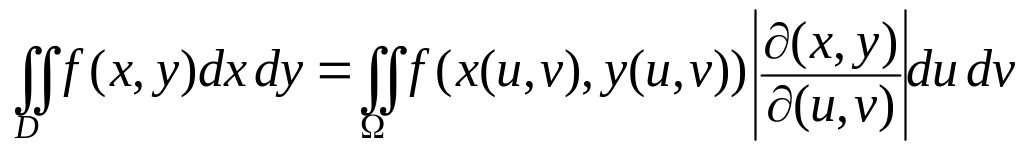Пример. Пусть область – сектор круга радиуса 1, расположенный между лучами .

Перейдем в интеграле к полярным координатам по формулам , учитывая, что . Мы получим

.

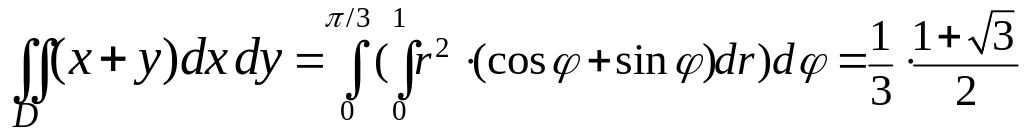Вычисление площади поверхности с помощью двойного интеграла.

В случае, когда уравнение поверхности задано в явном виде: , , площадь поверхности вычисляется по формуле

.

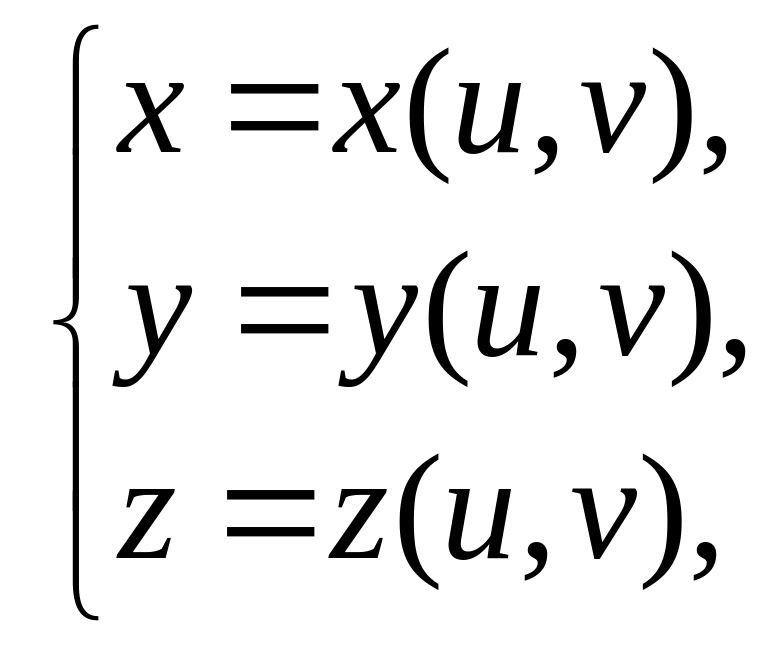
В том случае, когда поверхность задается параметрически: , площадь поверхности вычисляется по формуле

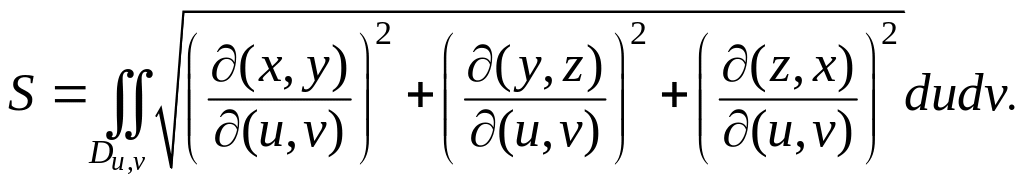
Тройные интегралы.

В качестве основной задачи, приводящей к тройному интегралу от функции трех переменных, рассмотрим задачу вычисления массы неоднородного тела с переменной плотностью .

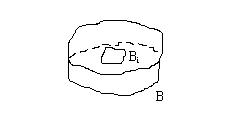
Разделим тело на фрагментов. Пусть - один из этих фрагментов. Выберем внутри этого фрагмента точку Обозначим через массу вещества внутри , через – объем . В силу непрерывности плотности при достаточно малых размерах фрагмента, то есть, при малых значениях можно считать, что Эти вычисления выполним для всех частей, на которые мы разбили тело. Складывая полученные произведения, найдем массу тела :

Точное значение массы найдем, если справа перейдем к пределу, когда число разбиений стремится к бесконечности, а все фрагменты стягиваются в точку, то есть наибольший из диаметров фрагментов, называемый диаметром разбиения, стремится к нулю:

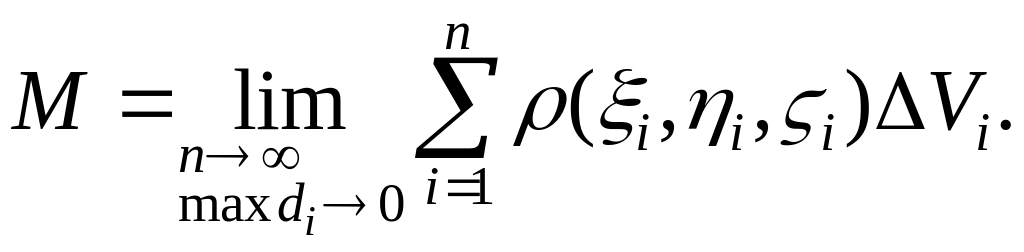
Предел интегральных сумм называется тройным интегралом от по области и обозначается . В данном случае функция положительна. В общем случае подынтегральная функция может произвольно менять знак.

Свойства тройного интеграла.

1. Тройной интеграл от суммы конечного числа функций равен сумме тройных интегралов от слагаемых функций

.

2. Постоянный множитель можно вынести за знак интеграла

3. Если всюду в , то

4. Если и есть соответственно наибольшее и наименьшее значения функции в трехмерной области , имеющей объем , то

.

5. Если функция непрерывная в трехмерной замкнутой области , то в этой области найдется по крайней мере одна точка для которой справедливо равенство

где площадь области (теорема о среднем).

6. Если трехмерная область разбита на две части и , то

.

Вычисление тройного интеграла.

Вычисление тройного интеграла, как и вычисление двойного интеграла, сводится к последовательным вычислениям интегралов по отрезкам.

Пусть любая прямая, параллельная оси OZ пересекает данное тело либо по одному отрезку, либо касается его в одной точке. Проекцией тела на плоскость XOY является область. Обозначим ее .

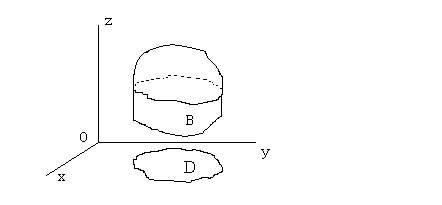
Пусть уравнения поверхностей, ограничивающих тело снизу и сверху (в направлении движения по оси OZ) соответственно, , и . Теперь тройной интеграл можно записать в виде двойного интеграла по области от интеграла по отрезку с переменными пределами:

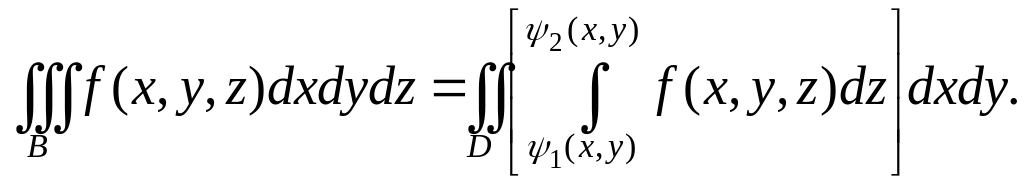
Пусть уравнения кривых, ограничивающих область снизу и сверху (в направлении движения вдоль оси OY) , и . Тогда .

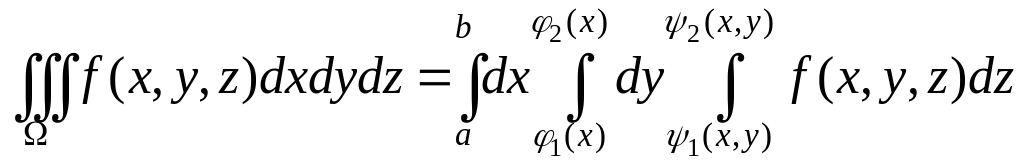Замена переменных в тройном интеграле.

Если переменные в тройном интеграле являются функциями переменных то тройной интеграл от функции по трехмерной области равен интегралу по области от функции , умноженной на модуль якобиана . То есть, справедлива формула

.

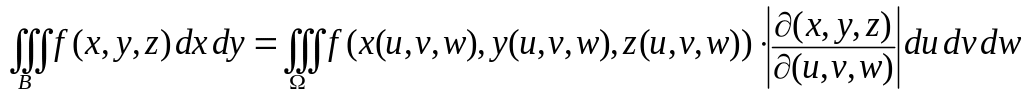Пример. Пусть трехмерная область – верхнее полушарие радиуса 1. Найти

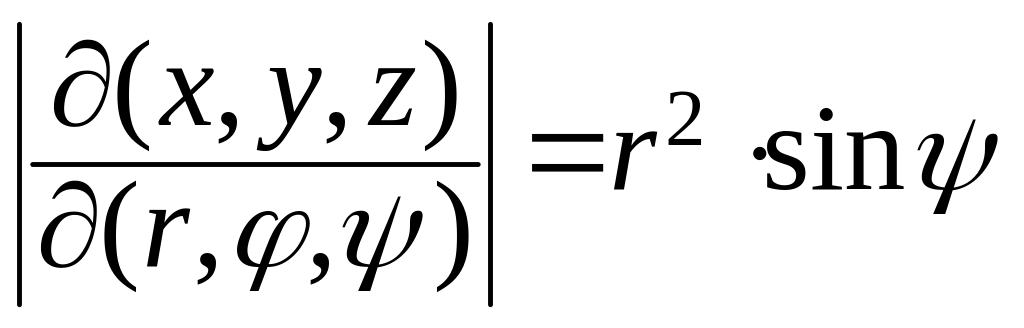. Перейдем к сферическим координатам по формулам . Учтем, что , и значит в верхнем полушарии . В результате расстановки пределов интегрирования получим

.
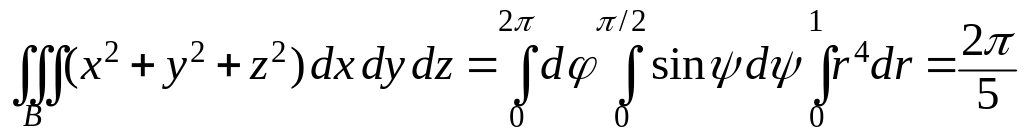