
- •Функции многих переменных
- •2. Найти . Переходя к сферическим координатам в окрестности точки , положим
- •Геометрический смысл частных производных функции двух переменных.
- •Касательная плоскость к поверхности, заданной в явном виде.
- •Якобиан.
- •2. Сосчитаем якобиан перехода от сферических координат к декартовым координатам. Напомним формулы:
- •Кратные интегралы
- •Замена переменных в двойном интеграле.
- •Вычисление тройного интеграла.
- •Криволинейные интегралы
- •Поверхностные интегралы
- •Поверхностный интеграл первого рода.
- •Связь интеграла по замкнутой поверхности с тройным интегралом по телу, ограниченному этой поверхностью. Формула Гаусса-Остроградского.
- •Элементы теории поля
- •Характеристики скалярного поля.
- •Характеристики векторного поля.
- •Оператор Гамильтона (набла-оператор).
- •Разложение произвольного векторного поля.
Якобиан.
Пусть
–
-мерная
вектор-функция
переменных, дифференцируемая в точке
.
В данном случае производная матрица
является квадратной, размера
![]() .
Для такой матрицы может быть вычислен
определитель. Этот определитель
.
Для такой матрицы может быть вычислен
определитель. Этот определитель
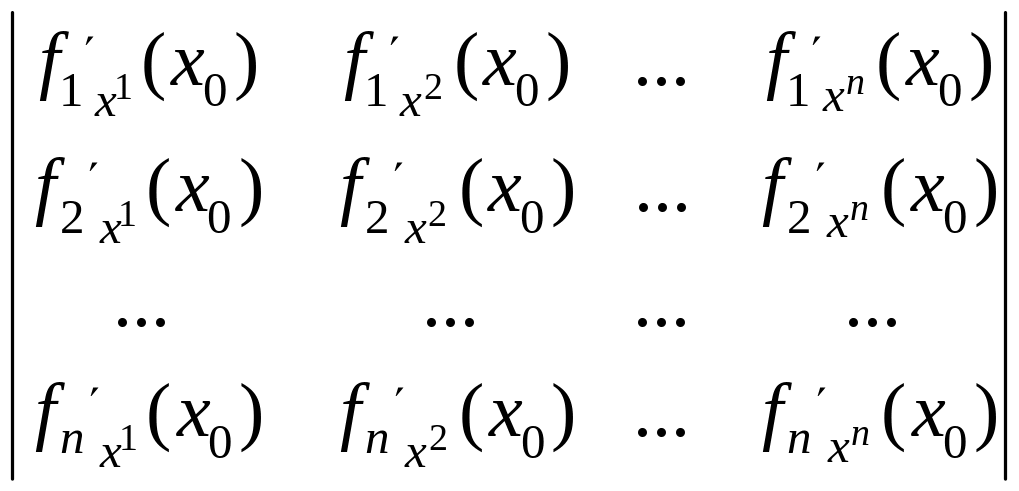 называется якобианом и обозначается
называется якобианом и обозначается
![]() .
.
Примеры.
1. Сосчитаем якобиан перехода от полярных
координат к декартовым координатам.
Напомним формулы:
.
Имеем
 .
.
2. Сосчитаем якобиан перехода от сферических координат к декартовым координатам. Напомним формулы:
![]() .
Имеем
.
Имеем
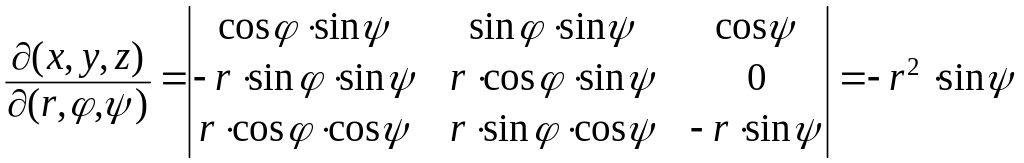 .
.
Касательная плоскость к поверхности, заданной параметрически.
Мы уже знаем, что
касательная плоскость к поверхности,
заданной явно в виде
![]() ,
в точке
,
в точке
![]() имеет уравнение
имеет уравнение
![]() .
.
Пусть теперь та
же поверхность задана параметрически:
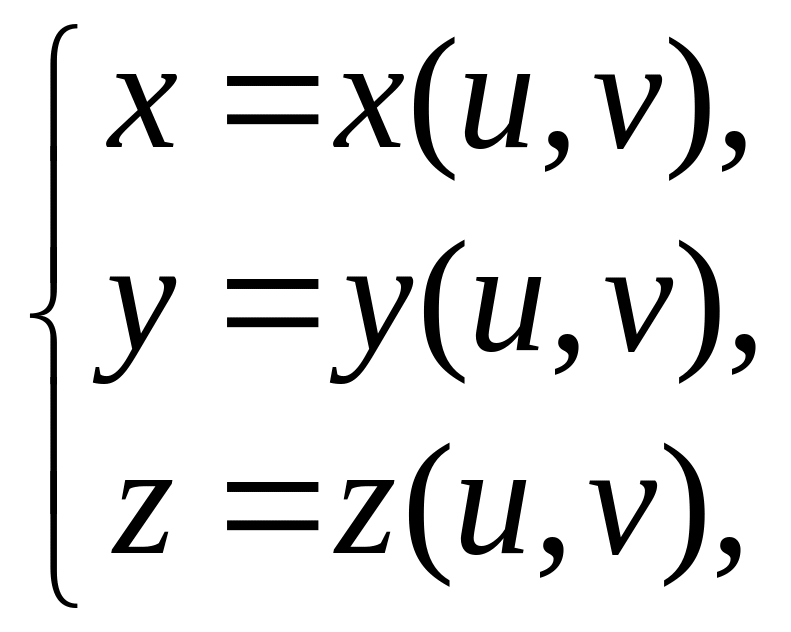
где
![]() – параметры, причем
– параметры, причем
![]() и
и
![]() .
.
В соответствии с
явным и параметрическим заданиями одной
и той же поверхности имеем
![]() .
Это значит, что мы имеем суперпозицию
функции двух переменных
.
Это значит, что мы имеем суперпозицию
функции двух переменных
![]() и вектор-функции
и вектор-функции
![]() .
Поэтому производная матрица-строка
.
Поэтому производная матрица-строка
![]() равна произведению матрицы-строки
равна произведению матрицы-строки
![]() на квадратную матрицу
на квадратную матрицу
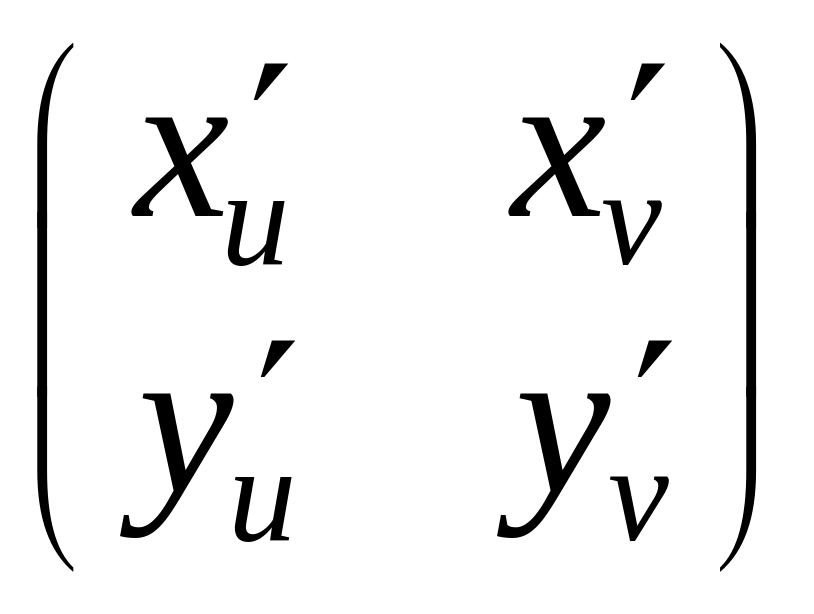 .
Сравнивая элементы одинаковых матриц,
получим
.
Сравнивая элементы одинаковых матриц,
получим
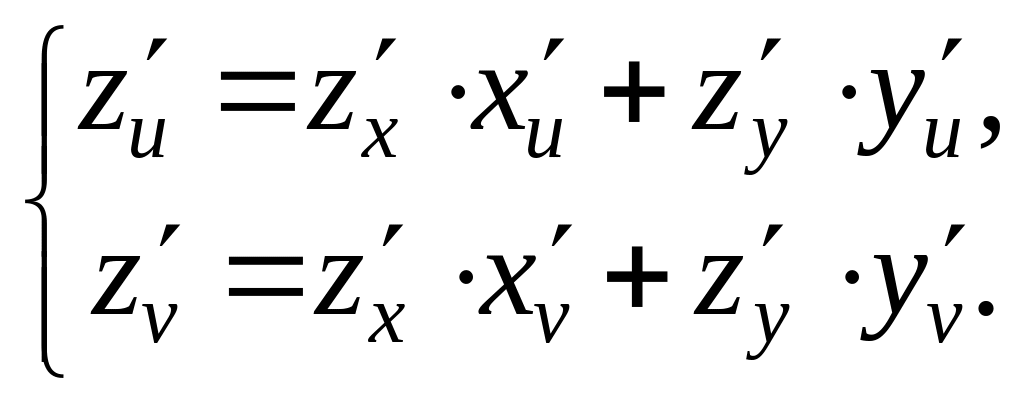
Последние соотношения
можно рассматривать как систему
относительно
![]() и
и
![]() .
Система с ненулевым главным определителем
имеет единственное решение, которое
можно найти с помощью правила Крамера:
.
Система с ненулевым главным определителем
имеет единственное решение, которое
можно найти с помощью правила Крамера:
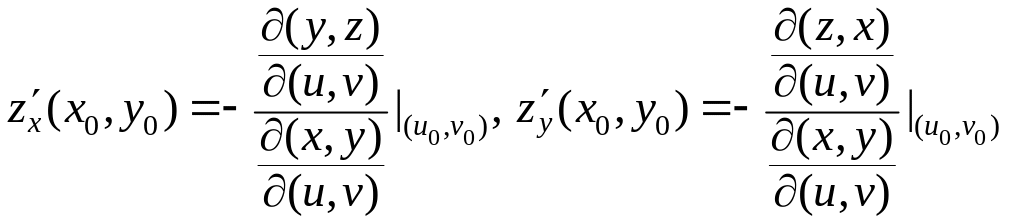 .
.
Подставляя полученные частные производные в уравнение касательной плоскости к поверхности, заданной в явном виде, получим уравнение касательной плоскости к поверхности, заданной параметрически:
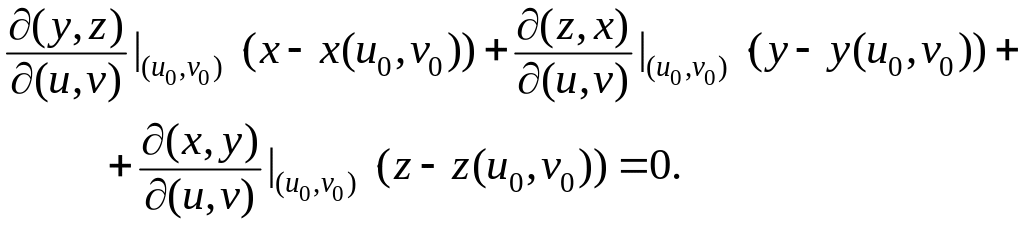
Производная по направлению.
Случай функции двух переменных
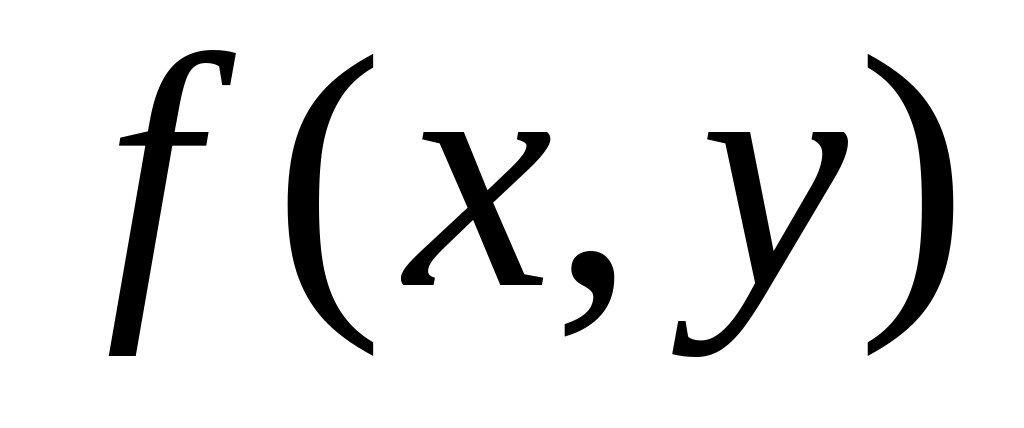 .
Направление задается вектором. Выберем
единичный вектор, задающий направление
на плоскости:
.
Направление задается вектором. Выберем
единичный вектор, задающий направление
на плоскости:
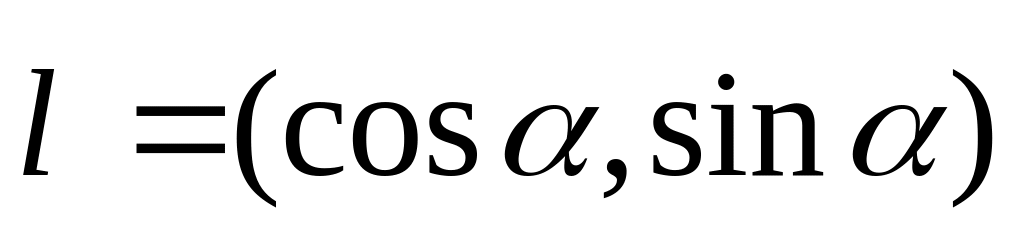 .
Этот вектор образует угол
с положительным направлением оси OX.
Производной функции двух переменных
по направлению
.
Этот вектор образует угол
с положительным направлением оси OX.
Производной функции двух переменных
по направлению
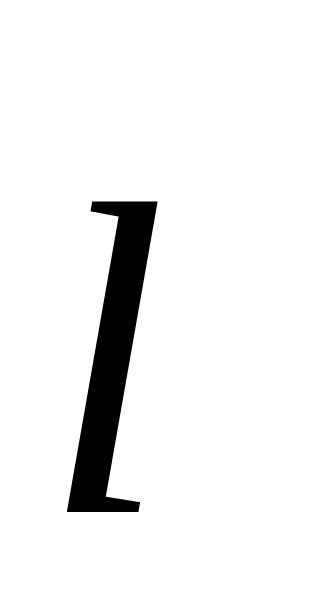 называется выражение
называется выражение
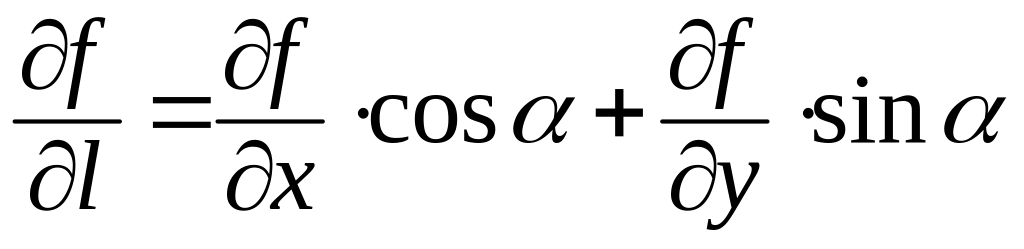 .
.Случай функции трех переменных
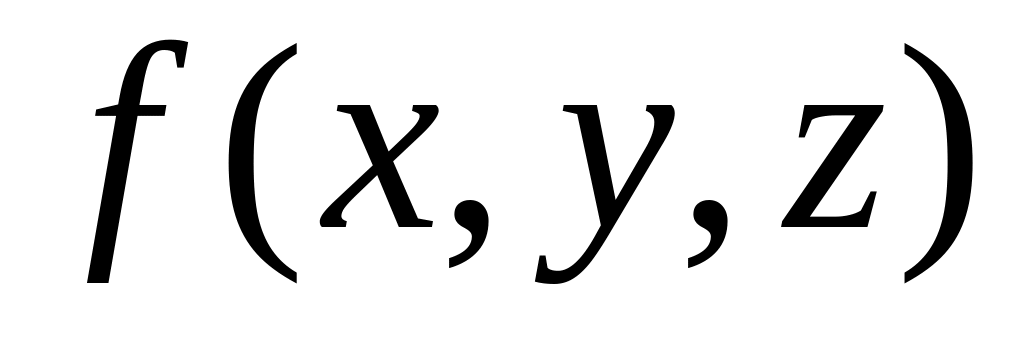 .
Пусть задан единичный вектор
,
образующий углы
.
Пусть задан единичный вектор
,
образующий углы
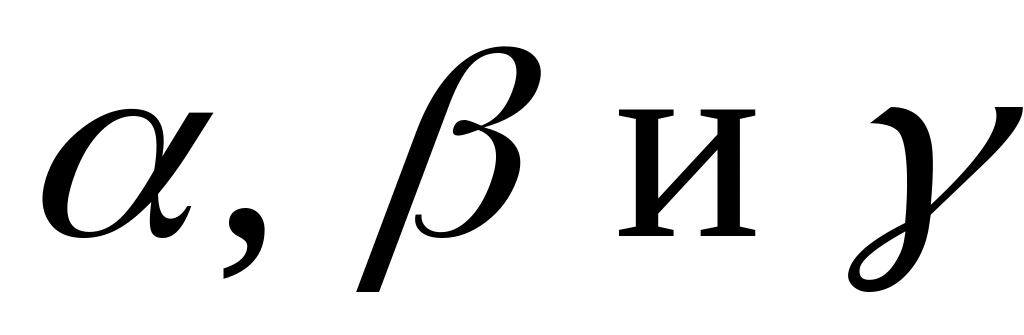 с осями OX,
OY
и OZ,
соответственно. Если обозначить
координаты вектора
через
с осями OX,
OY
и OZ,
соответственно. Если обозначить
координаты вектора
через
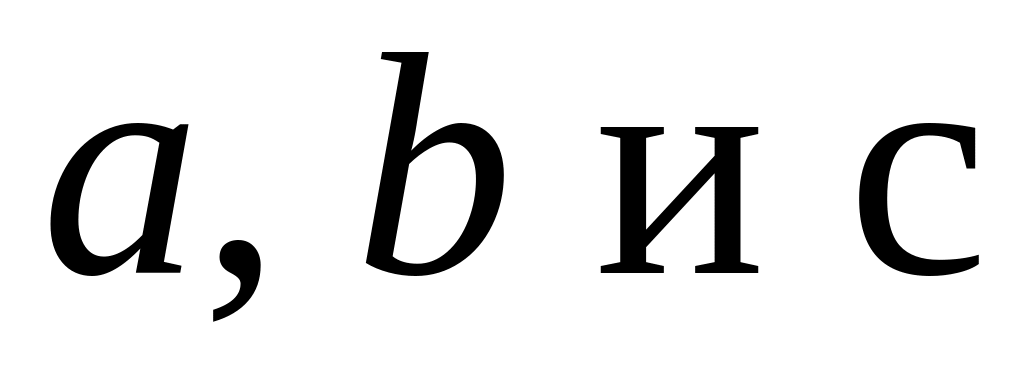 ,
то по формуле косинуса угла между двумя
векторами
и
,
то по формуле косинуса угла между двумя
векторами
и
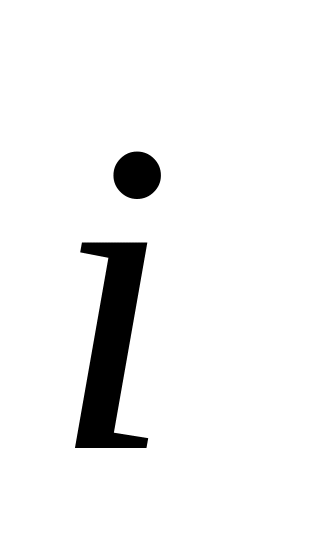 получим
получим
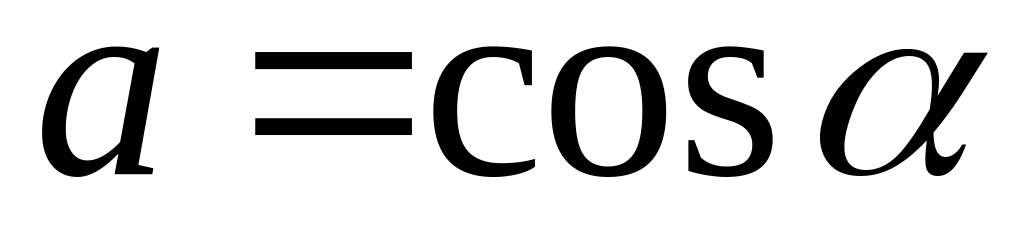 .
Аналогично,
.
Аналогично,
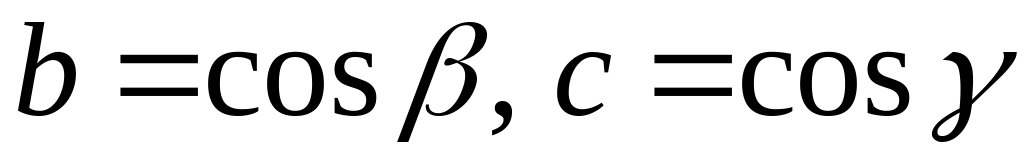 .
Таким образом, единичный вектор,
образующий углы
с осями OX,
OY
и OZ,
имеет координаты
.
Таким образом, единичный вектор,
образующий углы
с осями OX,
OY
и OZ,
имеет координаты
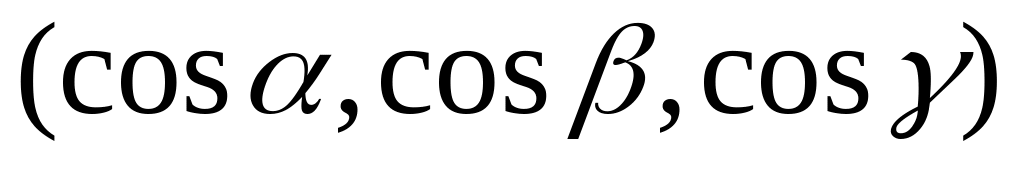 .
Производной функции трех переменных
по направлению
называется выражение
.
Производной функции трех переменных
по направлению
называется выражение
![]() .
.
Частные производные высших порядков.
Любая частная
производная
![]() функции
переменных
функции
переменных
![]() сама также является функцией
переменных. Частная производная от
частной производной функции многих
переменных называется частной
производной второго порядка
функции
.
При этом, если переменные, по которым
берутся производные сначала от функции
,
а затем от функции
,
не совпадают, такая частная производная
называется смешанной. Обозначения
частной производной второго порядка:
сама также является функцией
переменных. Частная производная от
частной производной функции многих
переменных называется частной
производной второго порядка
функции
.
При этом, если переменные, по которым
берутся производные сначала от функции
,
а затем от функции
,
не совпадают, такая частная производная
называется смешанной. Обозначения
частной производной второго порядка:
![]() .
В том случае, когда
.
В том случае, когда
![]() и
и
![]() –
непрерывные функции в окрестности
некоторой точки,
–
непрерывные функции в окрестности
некоторой точки,
![]() в этой точке.
в этой точке.
Аналогично вводятся частные производные любого порядка.
Дифференциалы высших порядков.
По аналогии с
производными вводятся дифференциалы
высших порядков, то есть дифференциалы
от дифференциалов. Рассмотрим функцию
трех переменных
![]() .
Дифференциалом этой функции является
выражение
.
Дифференциалом этой функции является
выражение
![]() .
Заметим, что входящие в последнее
выражение производные – функции от
.
Заметим, что входящие в последнее
выражение производные – функции от
![]() ,
а дифференциалы переменных не зависят
от
.
Поэтому при условии непрерывности
смешанных производных дифференциал
второго порядка имеет вид
,
а дифференциалы переменных не зависят
от
.
Поэтому при условии непрерывности
смешанных производных дифференциал
второго порядка имеет вид
![]()
![]()
![]() .
.
В последней формуле
мы воспользовались свойством равенства
смешенных производных. Нетрудно видеть,
что формула дифференциала второго
порядка аналогична формуле второй
степени суммы трех слагаемых. Нетрудно
сосчитать дифференциалы второго и
третьего порядков функции двух переменных
![]() :
:
![]() ,
,
![]() .
.
Формула Тейлора для функции многих переменных.
Как и в случае
функций одной переменной, для функций
многих переменных
![]() формула Тейлора дает связь между
приращением функции в точке и ее
дифференциалами в этой же точке:
формула Тейлора дает связь между
приращением функции в точке и ее
дифференциалами в этой же точке:
![]()
где
![]() .
.
В частности, для функции двух переменных имеем:
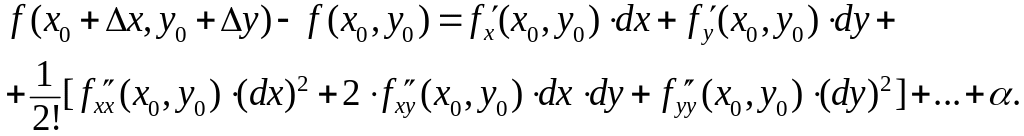
Здесь
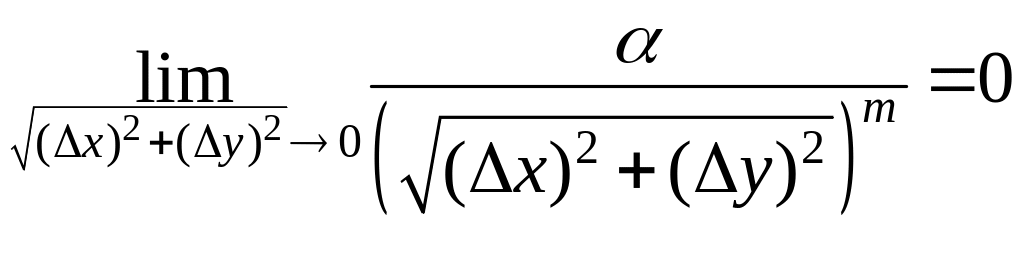 .
.
Локальный экстремум функции многих переменных.
Точкой локального
экстремума функции
![]() называется такая точка
называется такая точка![]() ,
для которой в области
существует окрестность, в которой
разность
,
для которой в области
существует окрестность, в которой
разность
![]() не меняет знак. В частности, точка
является точкой минимума, если
не меняет знак. В частности, точка
является точкой минимума, если
![]() ,
и точка
является точкой максимума, если
,
и точка
является точкой максимума, если
![]() .
.
Необходимое условие локального экстремума.
Пусть
– точка экстремума, и функция
дифференцируема в точке
.
Рассмотрим функцию одной переменной
![]() ,
где
– любое натуральное число между 1 и
.
Эта функция имеет точкой экстремума
точку
,
и значит,
,
где
– любое натуральное число между 1 и
.
Эта функция имеет точкой экстремума
точку
,
и значит,
![]() .
Следовательно, необходимым условием
экстремума функции многих переменных
в точке
,
где она дифференцируема, является
следующее условие:
.
Следовательно, необходимым условием
экстремума функции многих переменных
в точке
,
где она дифференцируема, является
следующее условие:
![]() .
Точка, в которой все частные производные
первого порядка данной функции равны
нулю, называется критической
точкой этой
функции.
.
Точка, в которой все частные производные
первого порядка данной функции равны
нулю, называется критической
точкой этой
функции.
Достаточное условие локального экстремума.
Выполнение необходимого условия экстремума не обязательно обеспечивает действительное наличие экстремума в точке, то есть, критическая точка функции может не быть точкой локального экстремума. В качестве примера рассмотрим функцию двух переменных . Критической точкой для этой функции является точка (0,0). Однако эта точка является не экстремальной, а седловой.
hypar.wxm
Для того чтобы
выяснить, достигается ли в критической
точке экстремум и какой, следует
обратиться к дифференциалу второго
порядка в этой точке. Итак, пусть
–
критическая точка для функции многих
переменных
.
В этом случае
![]() .
В соответствии с формулой Тейлора
.
В соответствии с формулой Тейлора
![]() где
где
![]() .
.
Поэтому знак
разности
в окрестности точки
определяется знаком дифференциала
второго порядка в точке
при всевозможных малых приращениях
![]() .
.
Рассмотрим случай
![]() .
Пусть критическая точка имеет координаты
.
Пусть критическая точка имеет координаты
![]() .
Рассмотрим приращение функции в
окрестности этой точки:
.
Рассмотрим приращение функции в
окрестности этой точки:
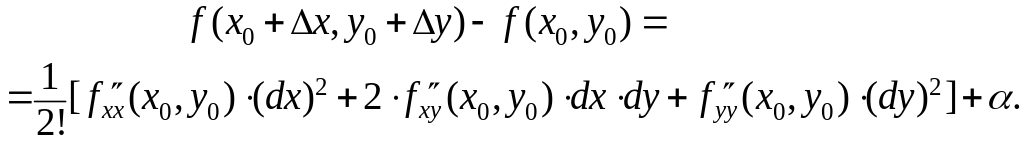
Если при любом
сочетании бесконечно малых приращений
![]() выражение в квадратных скобках не меняет
знак, то данная критическая точка
является точкой локального экстремума.
Вынесем за квадратную скобку множитель
выражение в квадратных скобках не меняет
знак, то данная критическая точка
является точкой локального экстремума.
Вынесем за квадратную скобку множитель
![]() .
Знак приращения функции совпадает со
знаком квадратного трехчлена
.
Знак приращения функции совпадает со
знаком квадратного трехчлена
![]() относительно
относительно
![]() .
Как известно, квадратный трехчлен не
меняет знак в том случае, если не имеет
корней, то есть если его дискриминант
отрицателен. В случае отрицательного
дискриминанта знак квадратного трехчлена
определяется знаком коэффициента при
наибольшей степени (или знаком свободного
члена). Таким образом, критическая
точка с координатами
является точкой локального экстремума,
если
.
Как известно, квадратный трехчлен не
меняет знак в том случае, если не имеет
корней, то есть если его дискриминант
отрицателен. В случае отрицательного
дискриминанта знак квадратного трехчлена
определяется знаком коэффициента при
наибольшей степени (или знаком свободного
члена). Таким образом, критическая
точка с координатами
является точкой локального экстремума,
если
![]() .
При этом мы имеем точку минимума, если
.
При этом мы имеем точку минимума, если
![]() ,
и точку максимума, если
,
и точку максимума, если
![]() .
.
