
- •Функции многих переменных
- •2. Найти . Переходя к сферическим координатам в окрестности точки , положим
- •Геометрический смысл частных производных функции двух переменных.
- •Касательная плоскость к поверхности, заданной в явном виде.
- •Якобиан.
- •2. Сосчитаем якобиан перехода от сферических координат к декартовым координатам. Напомним формулы:
- •Кратные интегралы
- •Замена переменных в двойном интеграле.
- •Вычисление тройного интеграла.
- •Криволинейные интегралы
- •Поверхностные интегралы
- •Поверхностный интеграл первого рода.
- •Связь интеграла по замкнутой поверхности с тройным интегралом по телу, ограниченному этой поверхностью. Формула Гаусса-Остроградского.
- •Элементы теории поля
- •Характеристики скалярного поля.
- •Характеристики векторного поля.
- •Оператор Гамильтона (набла-оператор).
- •Разложение произвольного векторного поля.
Функции многих переменных
С функциями двух
переменных мы встречались в разделе
«Аналитическая геометрия в пространстве»,
когда, например, знакомились с эллиптическим
параболоидом, имеющим уравнение
![]() ,
или с гиперболическим параболоидом,
имеющим уравнение
,
или с гиперболическим параболоидом,
имеющим уравнение
![]() .
Правые части приведенных выражений
являются функциями переменных
.
Правые части приведенных выражений
являются функциями переменных
![]() и
и
![]() .
Если график функции одной переменной
представляет собой плоскую кривую,
характеризующую зависимость функции
от переменной, то в случае двух переменных
такую характеристику зависимости
функции (
.
Если график функции одной переменной
представляет собой плоскую кривую,
характеризующую зависимость функции
от переменной, то в случае двух переменных
такую характеристику зависимости
функции (![]() )
от переменных (
и
)
выражает поверхность.
)
от переменных (
и
)
выражает поверхность.
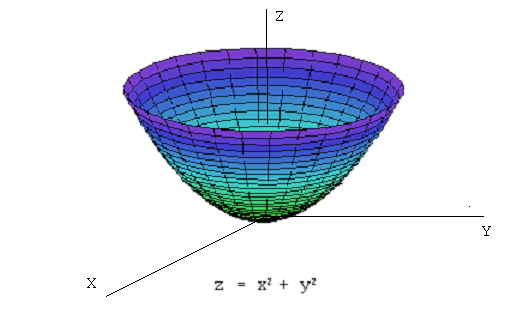
Для графического изображения зависимости функции трех и более переменных понадобилось бы пространство размерности, большей, чем 3. Поэтому такие графические изображения невозможны.
Многомерные пространства.
Мы будем рассматривать
![]() -мерные
пространства
-мерные
пространства
![]() ,
элементами которых являются точки
,
каждая из которых задается
координатами
,
элементами которых являются точки
,
каждая из которых задается
координатами
![]() .
В случае малой размерности пространства,
чтобы не вводить верхние индексы, мы
будем использовать традиционные
координаты:
.
В случае малой размерности пространства,
чтобы не вводить верхние индексы, мы
будем использовать традиционные
координаты:
![]() .
.
Расстоянием
между точками
и
-мерного
пространства является величина
![]() .
.
Функцией
переменных
![]() ,
заданной на множестве
,
заданной на множестве
![]() из
пространства
,
назовем закон, по которому каждой точке
из
пространства
,
назовем закон, по которому каждой точке
![]() ставится в соответствие вещественное
число
.
Примером функции двух переменных,
заданной на всей плоскости
ставится в соответствие вещественное
число
.
Примером функции двух переменных,
заданной на всей плоскости
![]() ,
является
уже
рассмотренная функция
,
графическая зависимость которой
изображается с помощью эллиптического
параболоида.
,
является
уже
рассмотренная функция
,
графическая зависимость которой
изображается с помощью эллиптического
параболоида.
Предел функции
многих переменных.
Понятие предела функции в точке
переносится с функций одной переменной
на функции многих переменных![]() следующим образом.
следующим образом.
![]() ,
если для любого
,
если для любого
![]() существует такое значение
существует такое значение
![]() ,
что для любых точек
,
таких что
,
что для любых точек
,
таких что
![]() ,
выполняется неравенство
,
выполняется неравенство
![]() .
.
В случае функций двух переменных для вычисления предела в точке удобно переходить к полярным координатам в окрестности этой точки, а в случае функции трех переменных – к сферическим координатам.
П р и м е р ы. 1. Найти
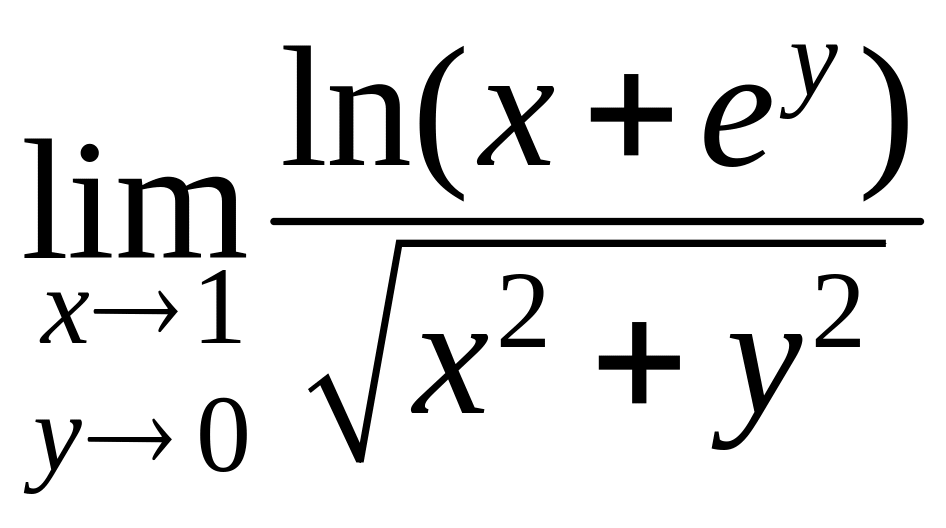 .
Переходя к полярным координатам в
окрестности точки
.
Переходя к полярным координатам в
окрестности точки
![]() ,
запишем
,
запишем
![]() .
Очевидно, что точка с координатами
.
Очевидно, что точка с координатами
![]() стремится к точке с координатами
тогда и только тогда, когда
стремится к точке с координатами
тогда и только тогда, когда
![]() .
Следовательно, искомый предел равен
.
Следовательно, искомый предел равен
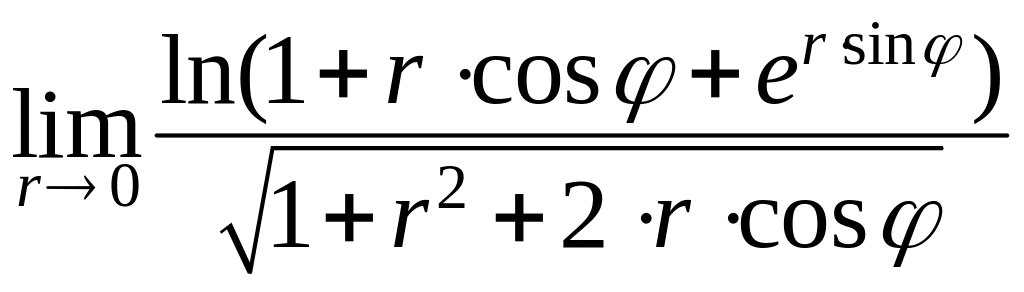 .
Последний предел – это предел функции
одной переменной
.
Последний предел – это предел функции
одной переменной
![]() ,
непрерывной по
при
,
непрерывной по
при
![]() для любого значения
для любого значения
![]() .
Поэтому мы получаем ответ:
.
Поэтому мы получаем ответ:
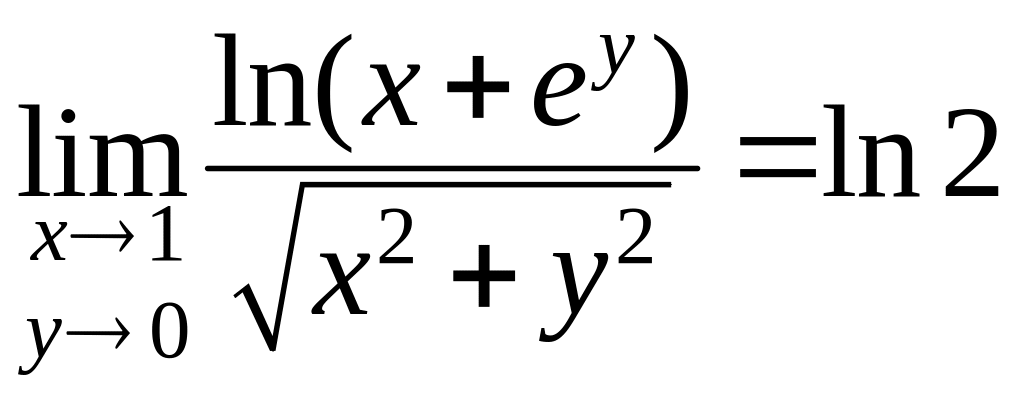 .
.
2. Найти . Переходя к сферическим координатам в окрестности точки , положим
![]() .
Точка с координатами
.
Точка с координатами
![]() стремится к точке
тогда и только тогда, когда
.
Следовательно, искомый предел после
перехода к сферическим координатам и
сокращения числителя и знаменателя на
величину
стремится к точке
тогда и только тогда, когда
.
Следовательно, искомый предел после
перехода к сферическим координатам и
сокращения числителя и знаменателя на
величину
![]() равен
равен
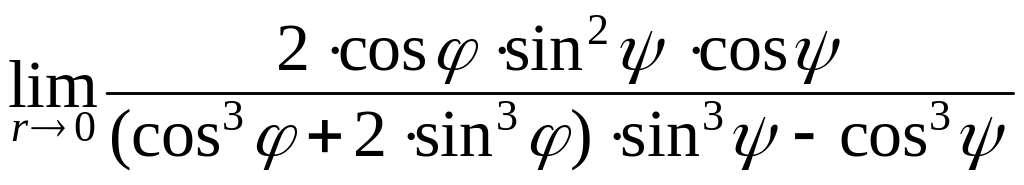 .
Очевидно, что данный предел не существует,
так как полученное после сокращения
выражение не зависит от переменной
,
а зависит только от значений
и
.
Очевидно, что данный предел не существует,
так как полученное после сокращения
выражение не зависит от переменной
,
а зависит только от значений
и
![]() .
Ответ: предел не существует.
.
Ответ: предел не существует.
Непрерывность
функции многих переменных в точке.
Как и в случае функций одной переменной,
функция многих переменных
называется непрерывной в точке
![]() ,
если точка
,
если точка
![]() входит в область определения функции
и
входит в область определения функции
и
![]() .
.
Из определения
предела функции многих переменных
следует, что в случае, когда функция
![]() непрерывна в точке
,
для любого
существует такое значение
,
что для любых точек
,
таких что
,
выполняется неравенство
непрерывна в точке
,
для любого
существует такое значение
,
что для любых точек
,
таких что
,
выполняется неравенство
![]() .
Таким образом, малым
приращениям аргумента
(в смысле расстояния в пространстве
)
у функции, непрерывной в точке,
соответствуют малые
приращения функции.
.
Таким образом, малым
приращениям аргумента
(в смысле расстояния в пространстве
)
у функции, непрерывной в точке,
соответствуют малые
приращения функции.
Как и в случае функций одной переменной, арифметические действия над непрерывными функциями не выводят из класса непрерывных функций, если нет деления на 0.
Дифференцируемость функции многих переменных.
Требование дифференцируемости функции многих переменных в точке является более сильным, чем требование непрерывности функции в точке, так как не только обеспечивается малость приращения функции при малом приращении аргумента. Условие дифференцируемости состоит в том, что приращение функции, соответствующее бесконечно малому приращению аргумента, является результатом линейного преобразования этого бесконечно малого приращения аргумента.
Вспомним, что
приращение аргумента функции многих
переменных является
-мерным
вектором, а линейное отображение
-мерного
вектора в пространство размерности 1
задается матрицей-строкой размера
![]() .
Поэтому условие дифференцируемости
функции многих переменных
.
Поэтому условие дифференцируемости
функции многих переменных
![]() в точке
формулируется следующим образом:
существует
матрица-строка
в точке
формулируется следующим образом:
существует
матрица-строка
![]() такая, что для любого вектора приращений
аргумента
такая, что для любого вектора приращений
аргумента![]() имеет место представление
имеет место представление
![]() ,
,
где величина
![]() настолько мала, что
настолько мала, что
![]() .
.
При этом матрица-строка
![]() называется
производной матрицей, а величина
называется
бесконечно малой более высокого порядка
по сравнению с расстоянием
называется
производной матрицей, а величина
называется
бесконечно малой более высокого порядка
по сравнению с расстоянием
![]() .
.
Частные производные.
Предположим, что
функция
дифференцируема в точке
.
Как выразить элементы производной
матрицы-строки
через заданную
функцию? Выберем вектор приращений
так, что приращения происходят только
по
![]() -му
аргументу
-му
аргументу
![]() .
Вектор приращений аргумента в этом
случае имеет вид
.
Вектор приращений аргумента в этом
случае имеет вид
![]() , следовательно,
, следовательно,
![]() .
Приращение функции примет вид
.
Приращение функции примет вид
![]() ,
где
,
где
![]() .
Последние соотношения являются условием
дифференцируемости функции
.
Последние соотношения являются условием
дифференцируемости функции
![]()
![]() одной
переменной
в точке
одной
переменной
в точке
![]() .
При этом
.
При этом
![]() .
.
Таким образом,
-й
элемент производной матрицы-строки
является производной по
-й
переменной
заданной функции в точке
при фиксированных остальных переменных
![]() .
Такая производная называется частной
производной функции многих переменных
.
Такая производная называется частной
производной функции многих переменных
![]() по переменной
в точке
по переменной
в точке
![]() и обозначается
и обозначается
![]() .
Итак, производная матрица-строка,
участвующая в определении условия
дифференцируемости функции многих
переменных в точке
,
состоит из частных производных по
соответствующим переменным в точке
:
.
Итак, производная матрица-строка,
участвующая в определении условия
дифференцируемости функции многих
переменных в точке
,
состоит из частных производных по
соответствующим переменным в точке
:
![]() .
.
Главная часть
приращения функции многих переменных
в точке
,
принимающая теперь вид
![]() ,
называется дифференциалом
функции
в точке
и обозначается
,
называется дифференциалом
функции
в точке
и обозначается
![]() .
Таким образом, связь приращения функции
в точке и дифференциала в той же точке
имеет вид
.
Таким образом, связь приращения функции
в точке и дифференциала в той же точке
имеет вид
![]() ,
где
– бесконечно
малая более высокого порядка по сравнению
с расстоянием
.
,
где
– бесконечно
малая более высокого порядка по сравнению
с расстоянием
.
