10. Проверка устойчивости замкнутой нескорректированной сау.

10.1. Проверим сначала устойчивость с помощью алгебраического критерия Гурвица.

10.1.1. Запишем характеристическое уравнение САУ, приравняв нулю его характеристический многочлен:

Очевидно, что определенные ранее коэффициенты характеристического многочлена становятся при этом коэффициентами характеристического уравнения.

10.1.2. Составим из этих коэффициентов матрицу Гурвица, используя следующие правила:

1. Матрица Гурвица есть квадратная матрица, составленная из коэффициентов характеристического уравнения замкнутой САУ.

2. Порядок матрицы Гурвица равен порядку характеристического уравнения.

3. Первая строка матрицы заполняется коэффициентами с нечетными индексами, вторая – с четными.

4. Последующие пары строк образуются смещением первой пары на 1, 2, … и т. д. Позиций вправо.

5. Свободные позиции матрицы заполняются нулями.

Для нашего случая матрица Гурвица принимает вид:

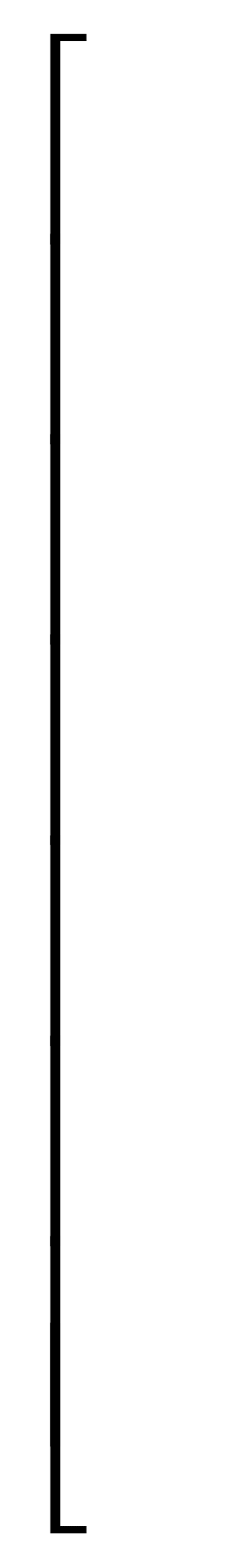
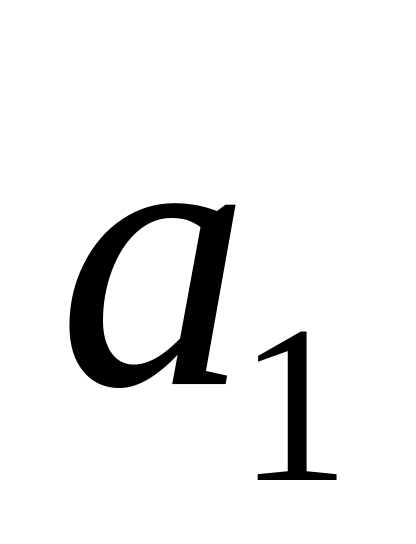
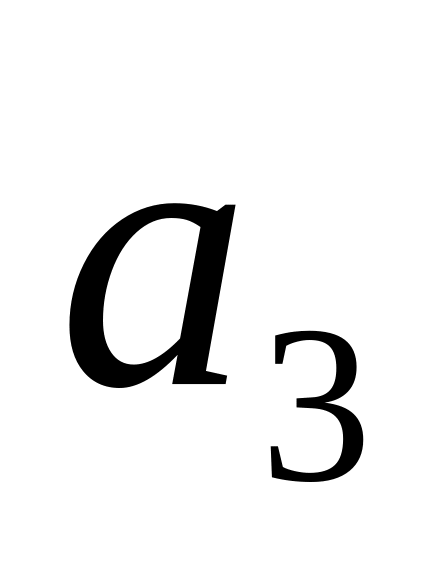
			0
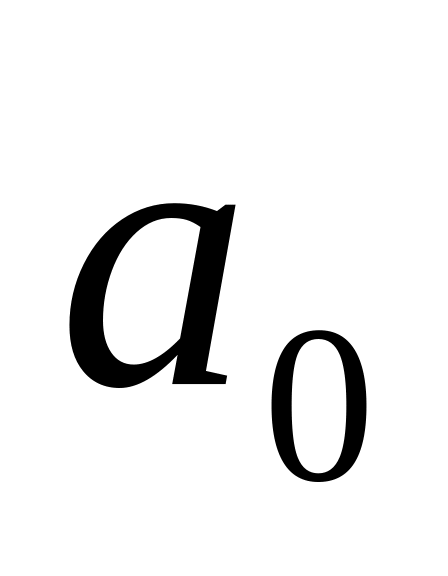
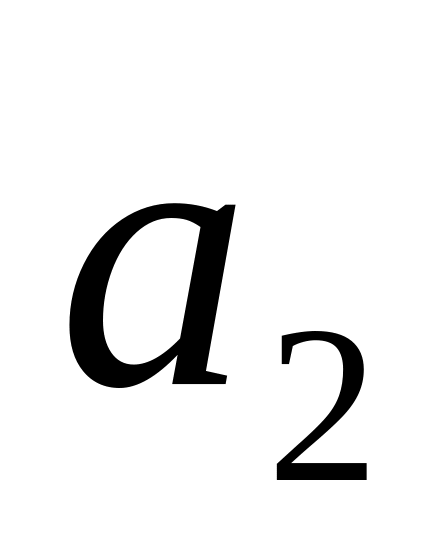
			0
	0

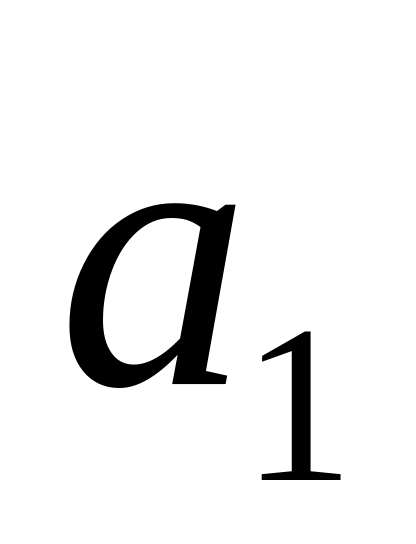
10.1.3. В соответствии с критерием Гурвица для устойчивости САУ необходимо и достаточно, чтобы при все определители Гурвица были положительны. В нашем случае эти условия принимают вид:

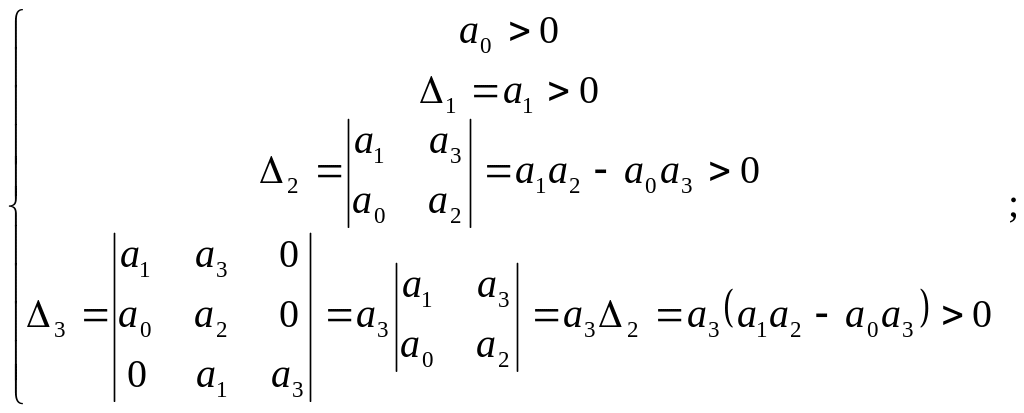
или

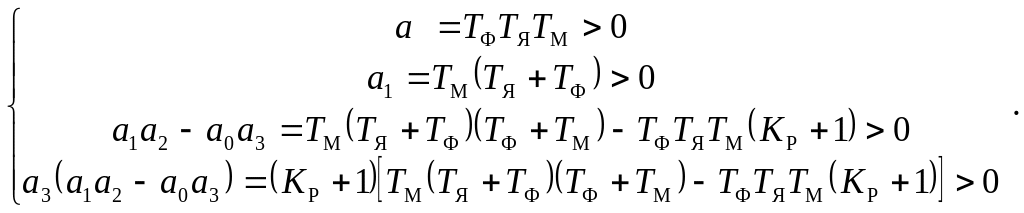
В случае , , , все эти неравенства будут одновременно справедливы, если справедливо неравенство:

которое и является условием устойчивости САУ по Гурвицу.

10.1.4. Для нашего случая:

Вывод: по Гурвицу замкнутая нескорректированная САУ устойчива/неустойчива.

10.2. Проверим далее устойчивость САУ с помощью частотных критериев.

Критерий Найквиста для логарифмических частотных характеристик

10.2.1. Рассчитаем и построим сначала логарифмическую шкалу частот, являющуюся осью абсцисс на плоскости логарифмических частотных характеристик (ПЛЧХ). Здесь вспомним, что логарифмическая шкала частот является, по сути дела, линейной шкалой десятичного логарифма угловой частоты , которая фактически оцифрована значениями этой частоты.

Рис. 1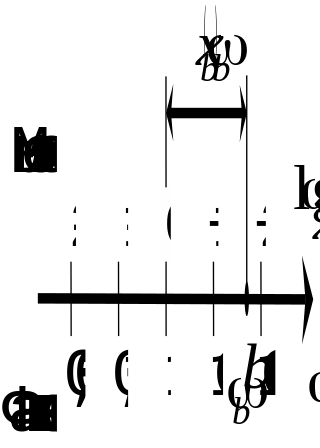

Для построения логарифмической шкалы частот мысленно проведем горизонтальную ось , на которую нанесем линейную шкалу для в соответствии с некоторым масштабом .

В этих условиях любая точка рассматриваемой оси будет определяться координатой (в миллиметрах), отсчитываемой от точки, в которой .

Для точки будет очевидно справедливо соотношение:

( 0 )

откуда следует, что:

( 0 )

и

( 0 )

Здесь - угловая частота, определяющая точку . Именно этой частотой должна быть фактически оцифрована точка на логарифмической шкале частот.

Для расчета оцифровки логарифмической шкалы частот удобно преобразовать выражение для к другому виду, положив, что:

где ;

.

Тогда:

Положив , из последнего выражения получаем:

Определим по этой формуле координаты всех оцифрованных точек логарифмической шкалы частот, представив результаты в виде таблицы.

Пример расчета для частоты выполним подробно.

, откуда

Координаты оцифрованных точек логарифмической шкалы частот:

	0,01	0,02	0,04	0,08	0,1	0,2	0,4	0,8

	1	2	4	8	10	20	40	80
	0

	100	200	400	800	1000	2000	4000	8000

Как видно из таблицы, частоте соответствует координата .

Это значит, что точка на шкале частот является точкой начала отсчета координаты .

Поэтому, задавшись на оси точкой , далее оцифровываем шкалу частот по данным таблицы.

10.2.2. Ось ординат плоскости логарифмических частотных характеристик (ПЛЧХ) может пересекать ось абсцисс в любой точке, поскольку на оси абсцисс принципиально отсутствует точка, соответствующая частоте ( ).

Примем для оси ординат следующие масштабы:

для модуля ;

для угла ;

и далее построим эту ось на плоскости логарифмических частотных характеристик (ПЛЧХ).

Рис. 2. Пример построения логарифмических частотных характеристик

10.2.3. Для случая используем представление передаточной функции разомкнутой системы в виде:

Перейдем к амплитудно-фазовой характеристике разомкнутой системы, положив в предыдущем выражении :

Амплитудно-фазовая характеристика разомкнутой САУ есть произведение амплитудно-фазовых характеристик динамических звеньев с передаточными функциями , , , .

10.2.4. Представим амплитудно-фазовые характеристики разомкнутой САУ и отдельных динамических звеньев в показательной форме записи:

( 0 )

Здесь:

, , , , - соответственно амплитудные частотные характеристики разомкнутой САУ, динамических звеньев с передаточными функциями , , , ;

, , , , - соответственно фазовые частотные характеристики разомкнутой системы, динамических звеньев с передаточными функциями , , , .

Сравнивая правую и левую части последнего равенства, получаем:

( 0 )

( 0 )

Амплитудно-частотная характеристика разомкнутой САУ есть произведение амплитудно-частотных характеристик динамических звеньев с передаточными функциями , , , .

Фазочастотная характеристика разомкнутой САУ есть сумма фазочастотных характеристик динамических звеньев с передаточными функциями , , , .

Последнее утверждение справедливо и по отношению к логарифмическим фазочастотным характеристикам (ЛФЧХ) разомкнутой системы и динамических звеньев с передаточными функциями , , , , так как ЛФЧХ отличаются от фазочастотных характеристик только использованием логарифмической шкалы частот на оси абсцисс вместо линейной.

10.2.5. Прологарифмируем правую и левую части выражения амплитудно-частотной характеристики по основанию 10:

( 0 )

Умножив обе части этого равенства на 20, перейдем к выражению логарифмической амплитудно-частотной характеристики (ЛАЧХ) разомкнутой системы:

или

( 0 )

Здесь ;

;

;

;

- соответственно ЛАЧХ разомкнутой системы и ЛАЧХ динамических звеньев с передаточными функциями , , , .

ЛАЧХ разомкнутой системы есть сумма ЛАЧХ динамических звеньев с передаточными функциями , , , .

10.2.6. Динамическое звено с передаточной функцией является безынерционным. Для такого звена:

Построим график функции на плоскости логарифмических частотных характеристик (ПЛЧХ).

10.2.7. Динамические звенья с передаточными функциями , , являются апериодическими.

Для этих звеньев будем строить ЛАЧХ упрощенно, используя так называемые асимптотические ЛАЧХ. Построение таких характеристик на плоскости логарифмических частотных характеристик ведут (для апериодических звеньев с обобщенной передаточной функцией ) по следующим правилам:

1. Асимптотическая ЛАЧХ представляет собой ломаную линию, составленную из двух сопряженных друг с другом лучей асимптот.

2. Левая асимптота горизонтальна и поднята над шкалой частот на уровень .

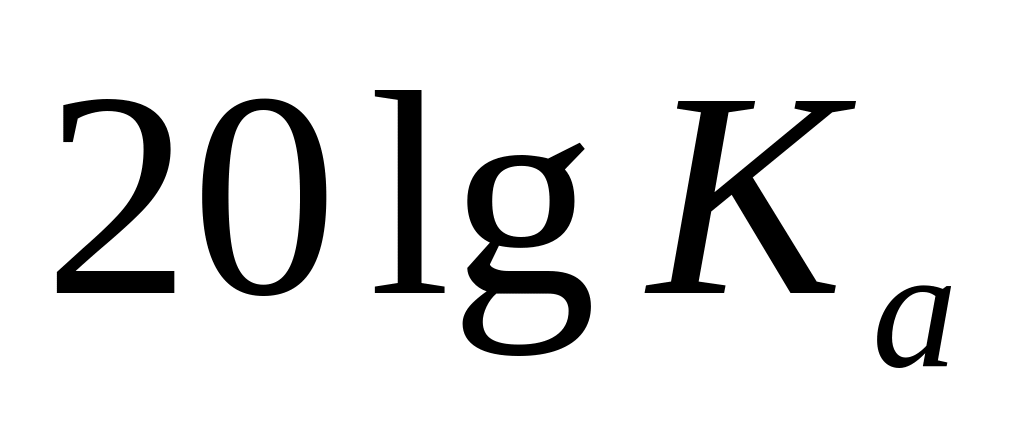3. Правая асимптота наклонена вправо и имеет коэффициент наклона .

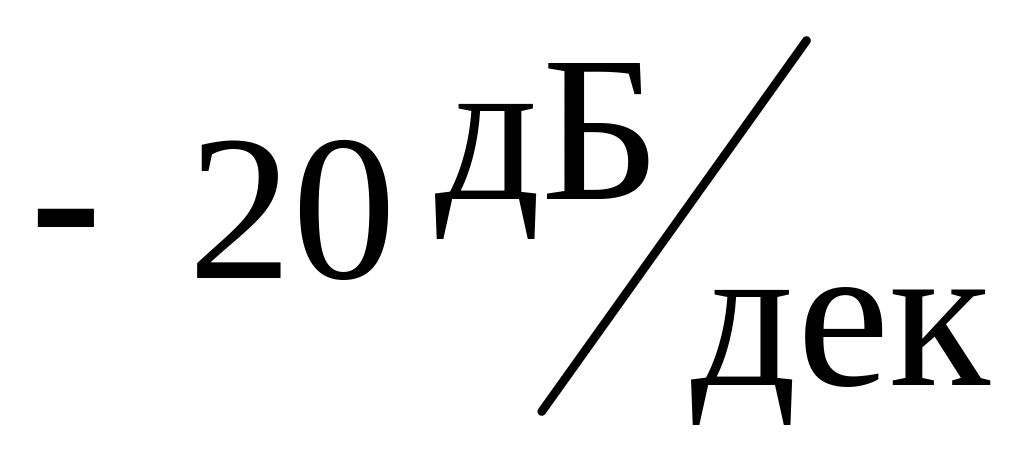4. Точка сопряжения асимптот характеризуется сопрягающей частотой .

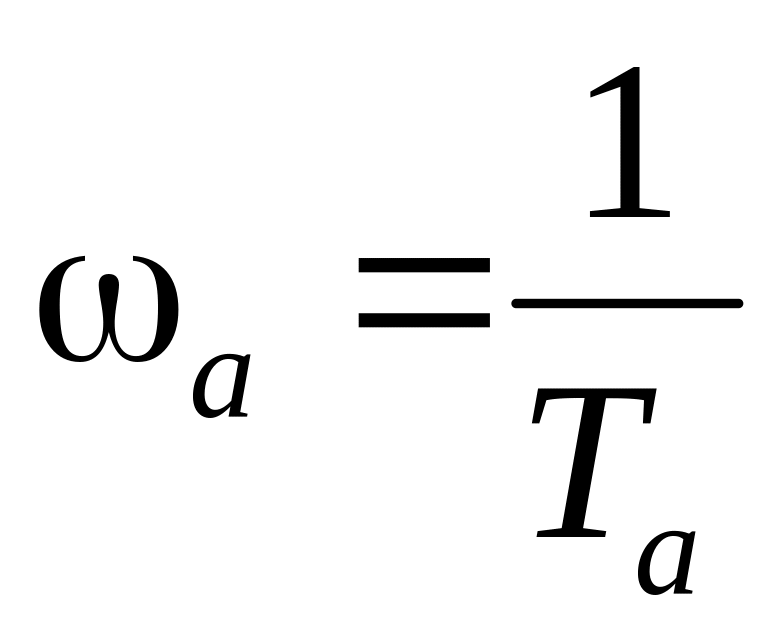Очевидно, что для всех апериодических звеньев нашего случая , то есть левая асимптота ЛАЧХ совпадает со шкалой частот.

Сопрягающие частоты асимптотических ЛАЧХ динамических звеньев с передаточными функциями , , определяются следующим образом:

Положение точек , и на логарифмической шкале частот относительно точки определим по соотношению, полученному в п. 10.2.1.:

Наклон для главных асимптот зададим специальным опорным отрезком AB с этим наклоном, построенным в левой части плоскости логарифмических частотных характеристик (ПЛЧХ).

Используя полученные расчетные данные и опорный отрезок, построим на плоскости логарифмических частотных характеристик (ПЛЧХ) асимптотические ЛАЧХ звеньев с передаточными функциями , , - , и соответственно.

10.2.8. Заменим ЛАЧХ апериодических звеньев в общем выражении ЛАЧХ разомкнутой системы (п.10.2.5) асимптотическими ЛАЧХ этих звеньев.

Тогда получим:

Построим на плоскости логарифмических частотных характеристик (ПЛЧХ) ЛАЧХ разомкнутой системы, графически складывая характеристики , , , .

10.2.9. Фазочастотная характеристика апериодического звена с обобщенной передаточной функцией имеет вид:

Для звеньев с передаточными функциями , , эта зависимость принимает вид:

10.2.10. Фазочастотная характеристика разомкнутой САУ тогда принимает вид:

Положив в последнем выражении , получаем:

Проводим далее расчет ЛФЧХ для всех оцифрованных точек логарифмической шкалы частот, занося частоту и результат в следующую таблицу.

	…	…	…	…	…	…	…	…	…	…
	…	…	…	…	…	…	…	…	…	…

По данным этой таблицы строим график ЛФЧХ на плоскости логарифмических частотных характеристик (ПЛЧХ).

В случае п. 10.2.3 … 10.2.9 выполняются аналогично с учетом принятого представления .

Дополнительно вводится пункт, аналогичный 10.2.7, посвященный построению асимптотической ЛАЧХ звена .

При расчете фазочастотных характеристик звена и разомкнутой системы иметь в виду, что для колебательного звена с обобщенной передаточной функцией ФЧХ определяется соотношением:

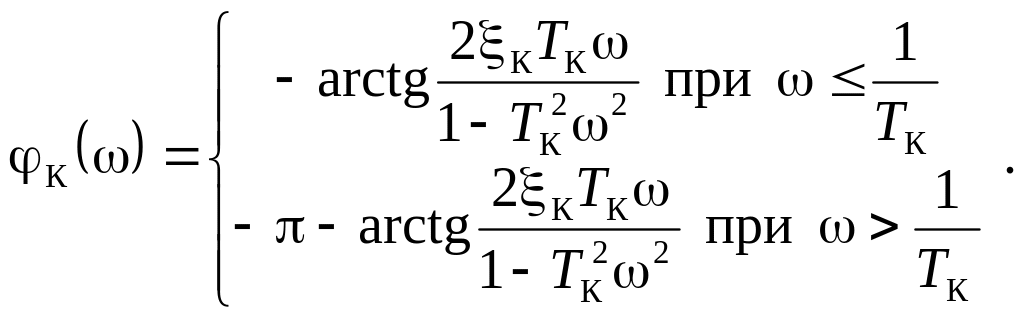
10.2.11. Найдем графически и отметим на ПЛЧХ точки логарифмической шкалы частот и , соответствующие решению уравнений:

.

Первая из этих точек изображает частоту среза разомкнутой нескорректированной системы, а вторая – частоту, на которой входной и выходной установившиеся синусоидальные сигналы в разомкнутой системе находятся в противофазе.

10.2.12. Используя критерий Найквиста для логарифмических частотных характеристик, видим, что замкнутая САУ устойчива/неустойчива по Найквисту, так как при монотонном характере :

10.2.13. В устойчивой САУ запасы устойчивости по модулю и фазе определяются соответственно соотношениями:

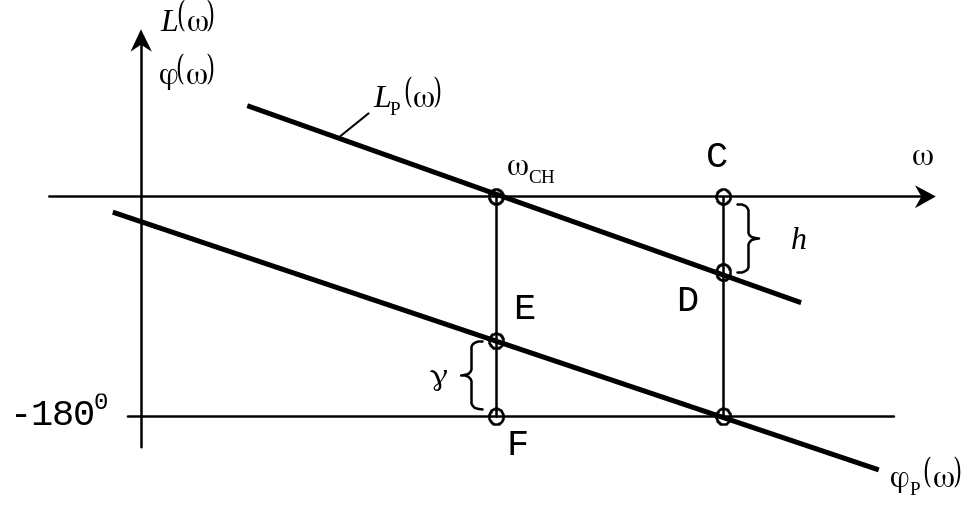
Рис. 3. Определение запасов устойчивости по ПЛЧХ.

Определяя эти запасы через длины отрезков CD и EF на ПЛЧХ, получаем:

В случае, если частота оказывается близкой к частоте , , , , следует уточнить положение ЛАЧХ в окрестности частоты , используя поправки к асимптотическим ЛАЧХ или расчет ЛАЧХ по точным формулам.

10.2.14. Для проверки правильности построения асимптотических ЛАЧХ построим точные ЛАЧХ разомкнутой системы, воспользовавшись средствами программного комплекса MatLab.

Для этого представим передаточную функцию разомкнутой системы, полученную в пункте 4 (преобразованную ‑ в пункте 5.2) в виде отношения двух полиномов с коэффициентами a_i и b_i:

.

Зададим эту передаточную функцию в командной строке MatLab, используя известные функции этого пакета.

Введем переменные num и den ‑ векторы коэффициентов числителя и знаменателя соответственно передаточной функции. Порядок написания коэффициентов следует соблюдть в порядке убывания степени s. Строка h=tf(num,den) создает передаточную функцию h с числителем num и знаменателем den.

Пример:

>> num=[125];

>> den=[0.000467 0.0228 0.318 1];

>> h=tf(num,den)

Transfer function:

125

---------------------------------------

0.000467 s^3 + 0.0228 s^2 + 0.318 s + 1

Далее используем функцию bode(h,’r’) для построение ЛАЧХ и ЛФЧХ. Набрав её в рабочем поле, получаем следующее:

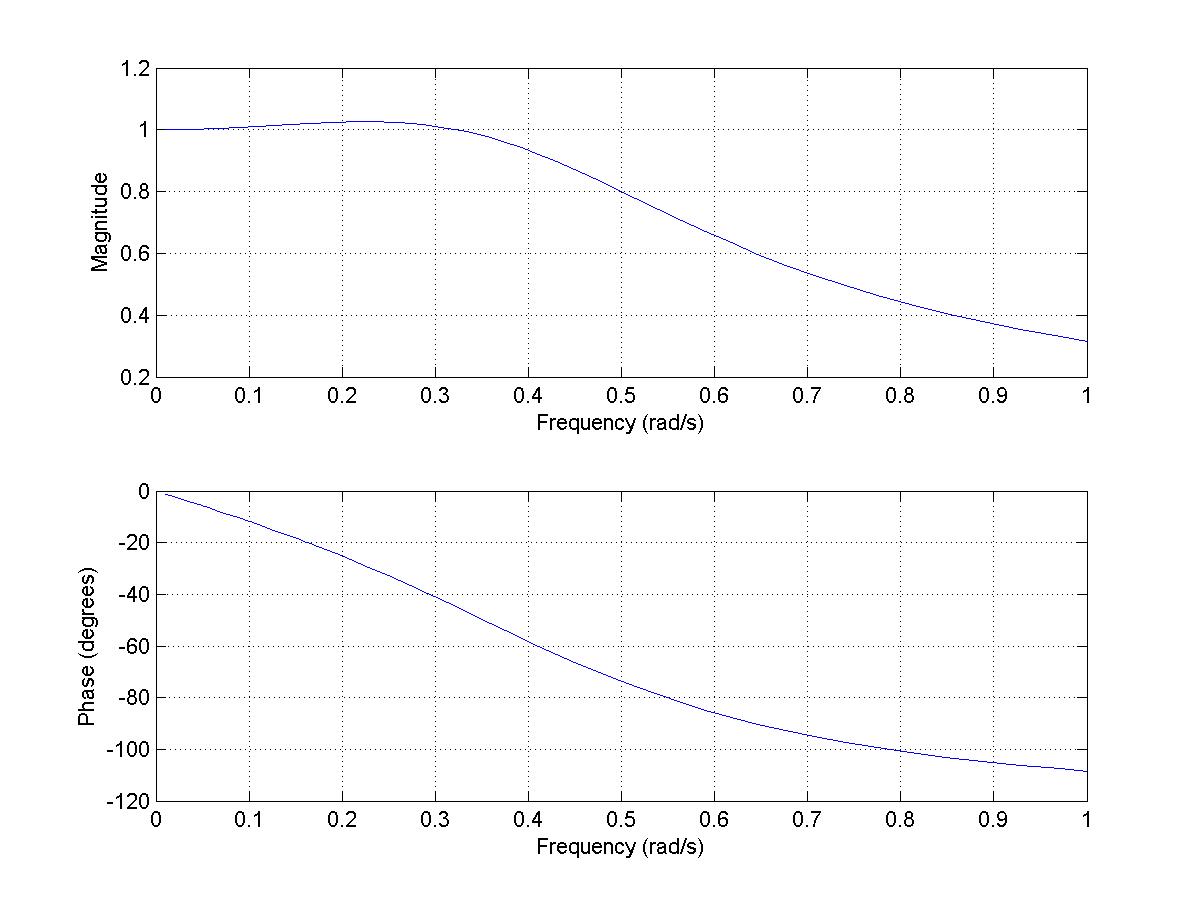
Возможно отредактировать вид осей в настройках осей(Axes propeties). По умолчанию Matlab делает формат осей логарифмическим. Приводим полученные графики и сравниваем их с асимптотическими ЛАЧХ, построенными вручную.