§ 7. Критерий согласия

Рассмотрим задачу проверки правдоподобия гипотез. Предположим, что мы хотим установить, противоречат ли опытные данные гипотезе о том, что случайная величина распределена по данному закону. Для ответа на такой вопрос пользуются так называемыми критериями согласия. Одним из наиболее часто применяемых является критерий Пирсона.

Изложим идею этого критерия сначала для случая дискретной с.в. с возможными значениями Предположим, что произведено независимых опытов, в каждом из которых с.в. приняла определенное значение. На основе этих опытов был составлен статистический ряд распределения с.в. :

(1)

где - частота события - число опытов, в которых появилось это событие . Выдвигаем гипотезу , состоящую в том, что с.в. имеет ряд распределения:

(2)

а отклонения частот от вероятностей объясняются случайными причинами. Чтобы проверить правдоподобность этой гипотезы, надо выбрать какую-то меру расхождения статистического распределения с гипотетическим.

В качестве меры расхождения между гипотетическим распределением и статистическим при использовании критерия берется сумма квадратов отклонений статистических вероятностей от гипотетических , взятых с некоторыми «весами» :

.

Коэффициенты вводятся потому, что отклонения, относящиеся к разным значениям , нельзя считать равноправными по значимости: одно и то же по абсолютной величине отклонение может быть малозначительным, если сама вероятность велика, и очень заметным, если она мала. Поэтому естественно «веса» взять обратно пропорциональными вероятностям . Пирсон доказал, что коэффициент пропорциональности должен быть следующим:

Таким образом, при большом числе опытов закон распределения величины обладает весьма простыми свойствами: он практически не зависит от закона распределения с.в. и мало зависит от числа опытов , а зависит только от числа значений с.в. и при увеличении приближается к распределению . При таком выборе коэффициентов мера расхождения обычно обозначается :

или, вводя величину под знаком суммы и учитывая, что , где - число значений в м разряде ; получим

Распределение , как известно, зависит от параметра , называемого «числом степеней свободы». При использовании этого критерия число степеней свободы полагается равным числу разрядов минус число независимых условий («связей»), наложенных на частоты Примерами таких условий могут быть:

если требуется только то, чтобы сумма частот была равна единице (это требование накладывается во всех случаях); или же

если требуется, чтобы совпадало статистическое среднее с гипотетическим, или же

если требуется, кроме того, еще и совпадение дисперсий и т.д.

Для распределения составлены таблицы. Пользуясь ими, можно для каждого значения и числа степеней свободы найти вероятность того, что величина, распределенная по закону , превзойдет это значение.

Распределение дает возможность оценить расхождение между гипотетическим распределением и статистическим. Если вероятность очень мала (не превосходит выбранного нами значения «уровня значимости» , такого, что событие с вероятностью считается уже практически невозможным), это значит, что опытные данные противоречат гипотезе , состоящей в том, что с.в. имеет распределение (2): эту гипотезу надо отбросить. Если же вероятность не мала, можно признать расхождения между теоретическим и гипотетическим распределениями несущественными и отнести их за счет случайных причин. Гипотезу можно считать правдоподобной, или, по крайней мере, не противоречащей опытным данным.

Подчеркнем, что большое значение вероятности (например, близкое к единице) отнюдь не свидетельствует о большом правдоподобии гипотезы . Это может говорить о том, например, что опытные данные сознательно «подгонялись» под желательное нам распределение (или просто о том, что число опытов недостаточно велико, чтобы распределение величины стало близко к ).

Критерий согласия можно применять и для непрерывных случайных величин, если, группируя статистический ряд, приближенно заменить непрерывную с.в. дискретной с возможными значениями где - середина -го разряда:

а - частота попадания с.в. в -й разряд ( );

Пусть мы хотим выровнять (сгладить) статистическое распределение с помощью гипотетической плотности . Будем поступать точно так же, как для дискретной с.в. , заменяя частоты их гипотетическими значениями: - т.е. вероятность попадания с.в. в - й разряд, вычисляемая по формуле 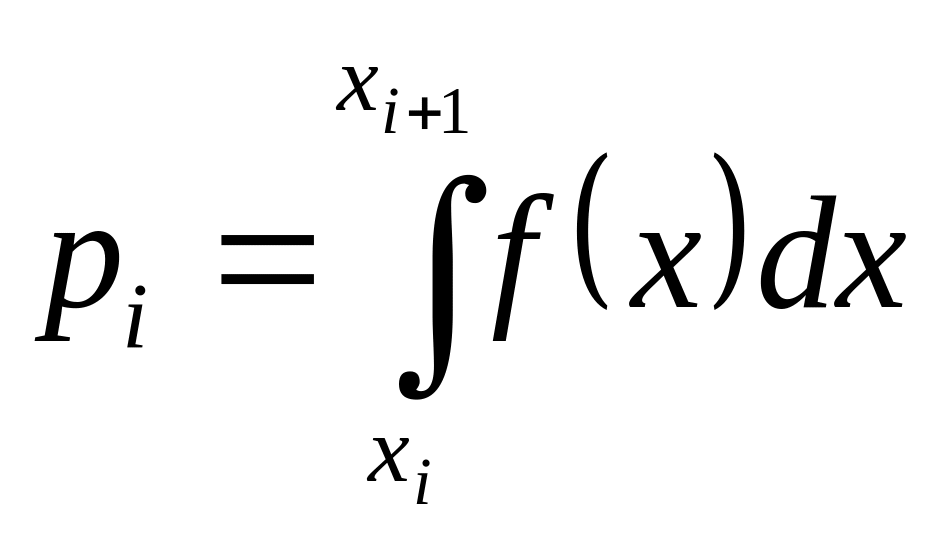; вместо числа значений с.в. берется число разрядов .

Во всем остальном поступаем и рассуждаем также, как для дискретной с.в.

Примеры с решениями

Пример 1. Произведено наблюдений над случайной величиной , возможные значения которой: Результаты 800 опытов представлены в виде таблицы ( - число появлений):

	0	1	2	3	4	5	6	7	8	9	10
	25	81	124	146	175	106	80	35	16	6	6

Требуется оценить правдоподобие гипотезы , состоящей в том, что распределена по закону Пуассона с параметром , равным статистическому среднему наблюденных значений с.в. . В качестве уровня значимости принять .

Решение. Разделив на , получим группированный статистический ряд:

	0	1	2	3	4
	0.031	0.101	0.155	0.183	0.219
	5	6	7	8	9	10
	0.132	0.100	0.044	0.020	0.008	0.008

Найдем статистическое среднее

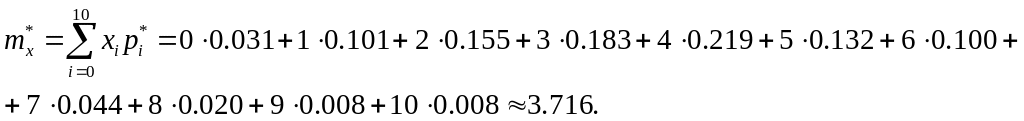
Вычислим вероятности , соответствующие закону Пуассона, по формуле

где

По найденному значению рассчитываем вероятности :

	0	1	2	3	4
	0.0243	0.0904	0.1680	0.2081	0.1933
	5	6	7	8	9	10
	0.1437	0.0890	0.0472	0.0219	0.0091	0.0033

Находим значение :

Число степеней свободы в данном случае равно числу значений случайной величины минус единица (первое условие: ) и минус еще единица – совпадение гипотетического математического ожидания со статистическим: По таблице значения распределения находим для и Таким образом, в данном примере гипотеза о пуассоновском распределении с.в. противоречит опытным данным и ее надо отбросить, так как достаточно мала.

Пример 2. Пользуясь критерием согласия Пирсона, определить не противоречат ли опытным данным гипотеза о том, что с.в. , имеющая статистическое распределение

Разряды	(-4) – (-3)	(-3) – (-2)	(-2) – (-1)	(-1) - 0
Частоты	0.012	0.050	0.144	0.266
Число попаданий в -й разряд	6	25	72	133
Разряды	0 ­- 1	1 - 2	2 - 3	3 - 4
Частоты	0.240	0.176	0.092	0.020
Число попаданий в -й разряд	120	88	46	10

распределена по нормальному закону с теми же математическим ожиданием и дисперсией, уровень значимости

Решение. Определяем число степеней свободы распределения , оно равно числу разрядов минус число наложенных связей: 1) ; 2) ; 3)

Составим таблицу вероятностей попаданий с.в. , подчиненной нормальному закону с параметрами и в разряды:

Разряды	(-4) – (-3)	(-3) – (-2)	(-2) – (-1)	(-1) - 0
Вероятности	0.0126	0.0522	0.1422	0.2433
Разряды	0 - 1	1 - 2	2 - 3	3 - 4
Вероятности	0.2668	0.1789	0.0770	0.0212

Пользуясь данными таблиц, вычислим значения

По таблице значений распределения при и находим значение это свидетельствует о том, что выдвинутая нами гипотеза о нормальности распределения с.в. не противоречит опытным данным.

Задачи

Задача 1. Используя критерий Пирсона, при уровне значимости 0.05 проверить, согласуется ли гипотеза о нормальном распределении генеральной совокупности с эмпирическим распределением выборки объема

Задача 2. Используя критерий Пирсона, при уровне значимости 0.01 установить, случайно или значимо расхождение между эмпирическими частотами , которые вычислены, исходя из гипотезы о нормальном распределении генеральной совокупности :