§ 2. Статистические оценки параметров распределения

Статистической оценкой неизвестного параметра теоретического распределения называют функцию от наблюдаемых случайных величин .

Точечной называют статистическую оценку, которая определяется одним числом , где ­- результаты наблюдений над количественным признаком (выборка).

Несмещенной называют точечную оценку, математическое ожидание которой равно оцениваемому параметру при любом объеме выборки:

Эффективной называют точечную оценку, обладающей минимальной дисперсией:

Состоятельной называют точечную оценку, которая при увеличении числа опытов приближается (сходится по вероятности) к искомому параметру:

Естественной оценкой для математического ожидания случайной величины является среднее арифметическое ее наблюденных значений (или статистическое среднее):

Эта оценка является состоятельной, эффективной и несмещенной.

Оценка

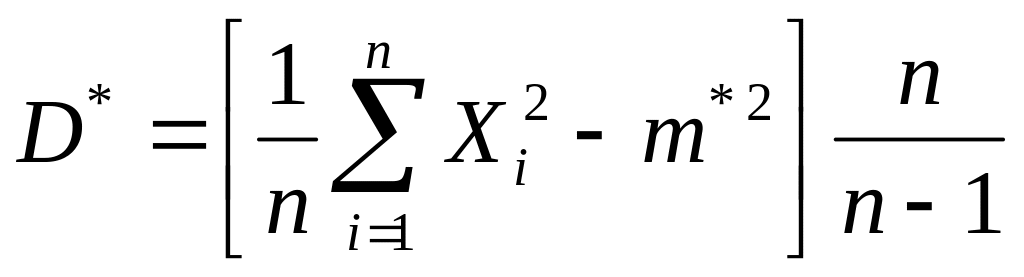
Является состоятельной и несмещенной для дисперсии .

Примеры с решениями

Пример 1. По данному распределению выборки объема найти несмещенную оценку математического ожидания.

наблюдаемые значения	2	5	7	10
частота	16	12	8	14

Решение. Несмещенной оценкой математического ожидания является статистическое среднее

Пример 2. По распределению выборки из предыдущего примера найти несмещенную оценку для дисперсии.

Решение. Несмещенной оценкой для дисперсии является оценка

В качестве статистического среднего использовали значение, полученное в предыдущем примере.

Задачи

Задача 1. Из генеральной совокупности извлечена выборка объема

наблюдаемые значения	1	3	6	26
частота	8	40	10	2

Найти несмещенную оценку генеральной средней.

§ 3. Метод моментов

Метод моментов точечной оценки неизвестных параметров заданного распределения состоит в приравнивании теоретических моментов соответствующим эмпирическим моментам того же порядка.

Если распределение определяется одним параметром, то для его отыскания приравнивают один теоретический момент одному эмпирическому моменту того же порядка. Например, можно приравнять начальный теоретический момент первого порядка начальному эмпирическому моменту первого порядка:

. (1)

Математическое ожидание является функцией от неизвестного параметра заданного распределения, поэтому, решив уравнение (1) относительно неизвестного параметра, получим его точечную оценку.

Если распределение определяется двумя параметрами, то приравнивают два теоретических момента двум соответствующим эмпирическим моментам того же порядка.

Например,

(2)

Левые части этих равенств являются функциями от неизвестных параметров, поэтому, решив систему (2) относительно неизвестных параметров, получим их точечные оценки.

Примеры с решениями

Пример 1. Случайная величина распределена по закону Пуассона

где -число испытаний, произведенных в одном опыте, - число появлений события в -м опыте. Найти методом моментов по выборке точечную оценку неизвестного параметра , определяющего распределение Пуассона.

Решение. Требуется оценить один параметр, поэтому достаточно иметь одно уравнение относительно этого параметра. Приравниваем начальный теоретический момент первого порядка начальному эмпирическому моменту первого порядка :

Приняв во внимание, что получим Учитывая, что математическое ожидание распределения Пуассона равно параметру этого распределения, имеем

Таким образом, точечной оценкой параметра распределения Пуассона служит выборочная средняя:

Пример 2. Найти методом моментов по выборке точечные оценки неизвестных параметров и гамма-распределения, плотность которого

.

Решение. Для отыскания двух неизвестных параметров необходимо иметь два уравнения; приравняем начальный теоретический момент первого порядка начальному эмпирическому моменту первого порядка и центральный теоретический момент второго порядка центральному эмпирическому моменту второго порядка

Учитывая, что имеем

Математическое ожидание и дисперсия гамма-распределения соответственно равны следовательно

Решив эту систему, получим искомые точечные оценки неизвестных параметров:

Пример 3. Случайная величина имеет геометрическое распределение:

где - число испытаний, произведенных до появления события, - вероятность появления события в одном испытании, . Найти методом моментов точечную оценку параметра .

Решение. Для геометрического распределения имеем следующий ряд распределения

Учитывая, что , получаем

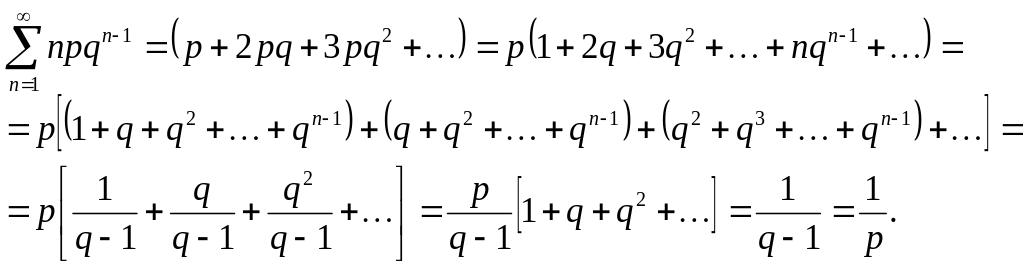
Таким образом, следовательно

.

Задачи

Задача 1. Найти методом моментов по выборке точечные оценки неизвестных параметров и нормального распределения, плотность которого

Задача 2. Устройство состоит из элементов, время безотказной работы которых подчинено гамма-распределению. Испытания пяти элементов дали следующие наработки (время работы элемента в часах до отказа): 50, 75, 125, 250, 300. Найти методом моментов точечные оценки неизвестных параметров и , которыми определяется гамма-распределение.

Задача 3. Случайная величина (число нестандартных изделий в партии) распределена по закону Пуассона. Ниже приведено распределение нестандартных изделий в партиях (в первой строке указано количество нестандартных изделий в одной партии, во второй строке указана частота - число партий, содержащих нестандартных изделий):

Найти методом моментов точечную оценку неизвестного параметра распределения Пуассона.

Задача 4. Найти методом моментов по выборке точечную оценку неизвестного параметра показательного распределения, плотность которого