§ 6. Вероятностные распределения, применяемые в статистике: гамма-распределение, распределение , распределение Стьюдента

Данные распределения возникают в статистике при анализе различных функций от конечной суммы случайных величин, каждая из которых является элементом некоторой выборки.

Производящая функция моментов. Данная функция представляет собой способ задания вероятностных распределений. Производящая функция используется чаще всего для вычисления моментов. Пусть есть случайная величина с известным распределением. Тогда её производящей функцией моментов называется функция, имеющая вид

.

Если случайная величина дискретна, то есть , то

Если случайная величина непрерывна, то есть задана плотность , то

.

Для вычисления моментов с помощью производящей функции используется следующая формула

.

Гамма-распределение. Данное распределение представляет собой двухпараметрическое семейство абсолютно непрерывных распределений.

Пусть распределение случайной величины задаётся плотностью вероятности, имеющей вид

где - гамма-функция Эйлера, тогда говорят, что случайная величина имеет гамма-распределение с параметрами и . Пишут ~ .

При различных значениях параметров и распределение и распределение Стьюдента являются частными случаями гамма-распределения.

Свойства гамма-распределения.

1. Если 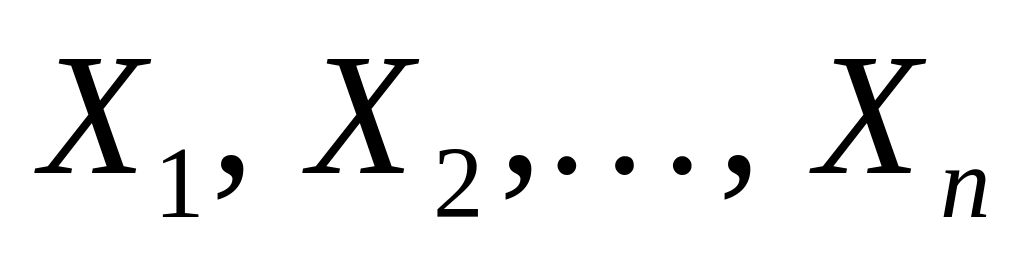- независимые случайные величины, такие что 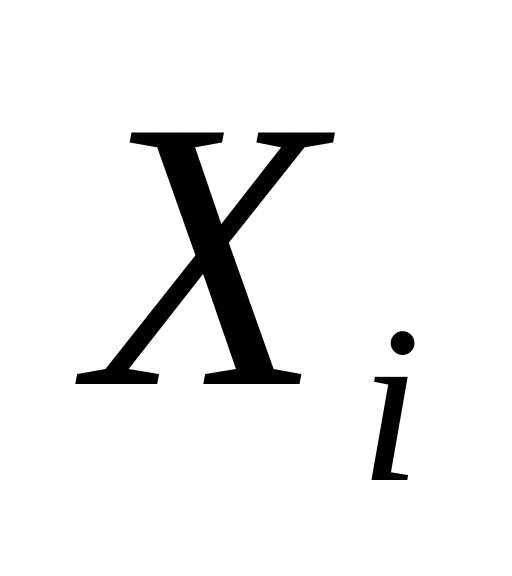~ 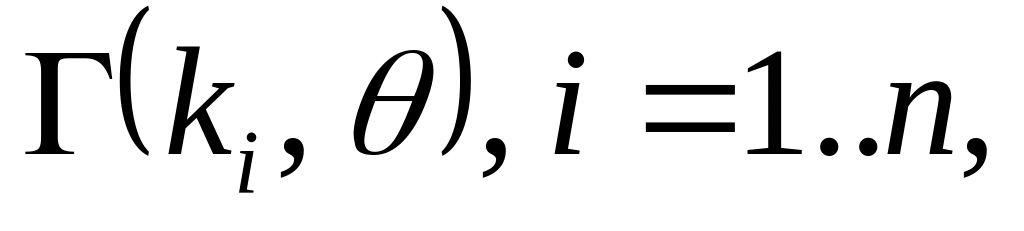то ~ .

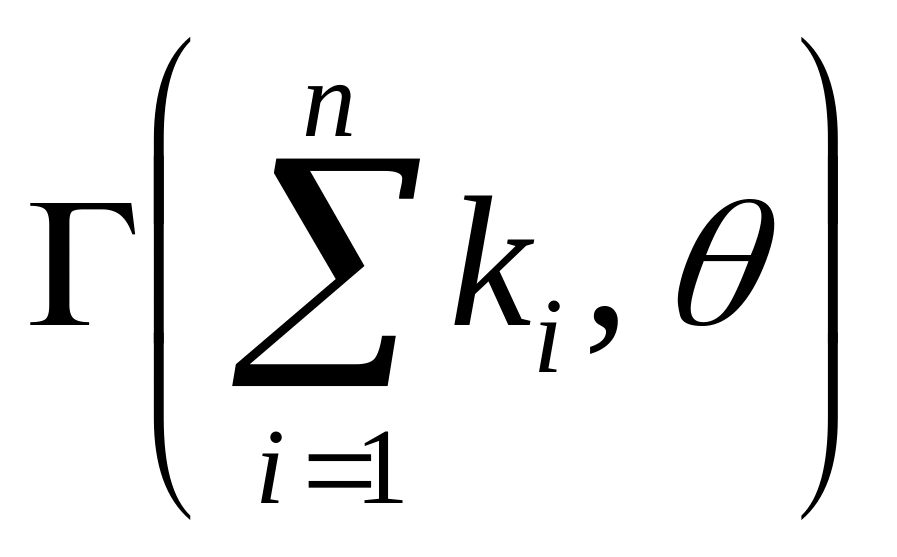2. Если ~ , и 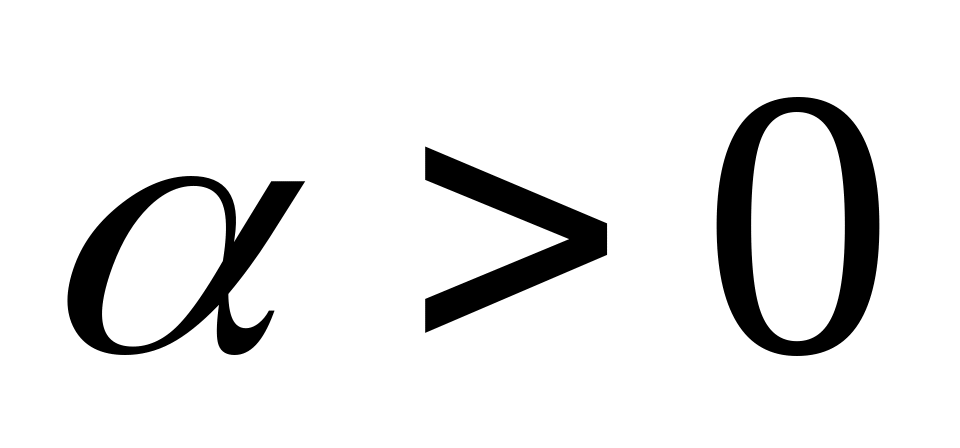- произвольная константа, то ~ .

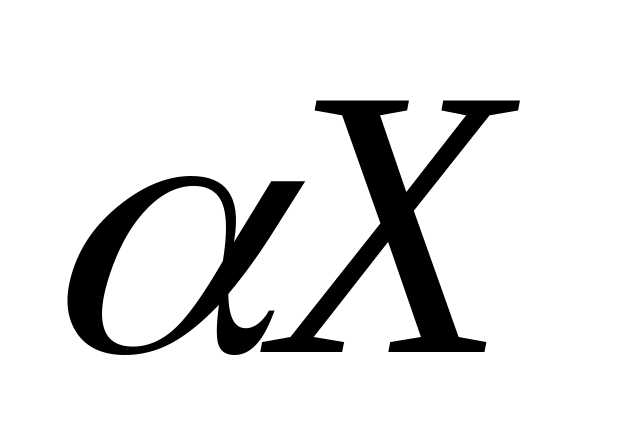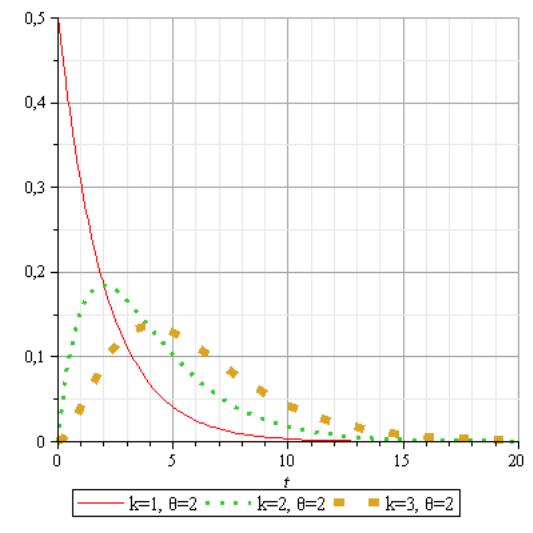
Распределение . Данное распределение является частным случаем гамма-распределения

Распределение с степенями свободы - это распределение суммы квадратов независимых стандартных нормальных случайных величин.

Пусть - совместно независимые стандартные нормальные случайные величины, то есть ~ . Тогда случайная величина имеет распределение с степенями свободы.

Найдем плотность распределения , используя технику производящих функций. Плотность распределения стандартной нормально распределенной случайной величины имеет вид

Используя определение производящей функции, получаем для случайной величины

Поскольку - совместно независимые случайные величины, получаем производящую функцию для случайной величины

Выпишем теперь производящую функцию для гамма-распределения

сделаем замену

тогда

.

Очевидно, что при значении параметров производящая функция гамма-распределения совпадает с полученным ранее выражением для производящей функции распределения .

Подставляя найденные значения параметров в выражение для плотности распределения гамма-распределения, получаем плотность распределения .

Таким образом, плотность распределения имеет вид

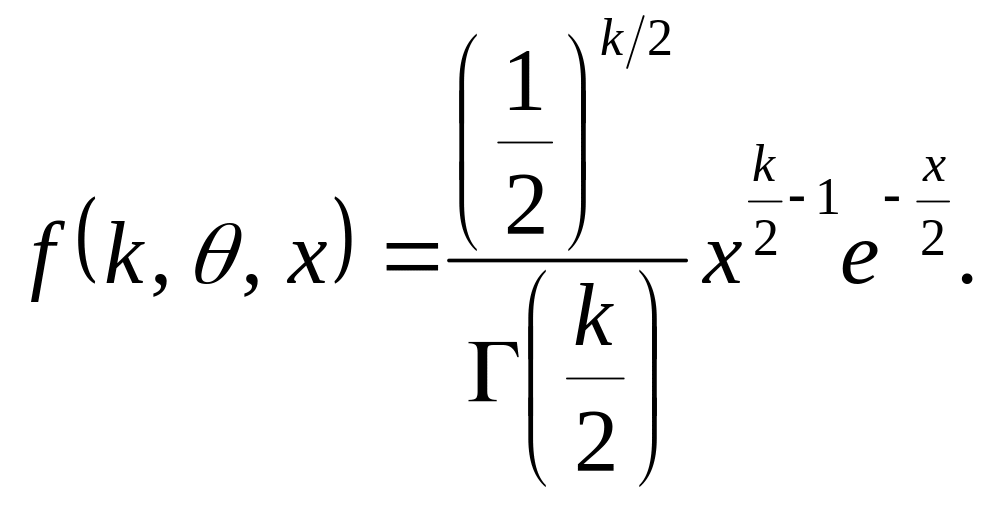
Свойства распределения .

1. Распределение устойчиво относительно суммирования. Если 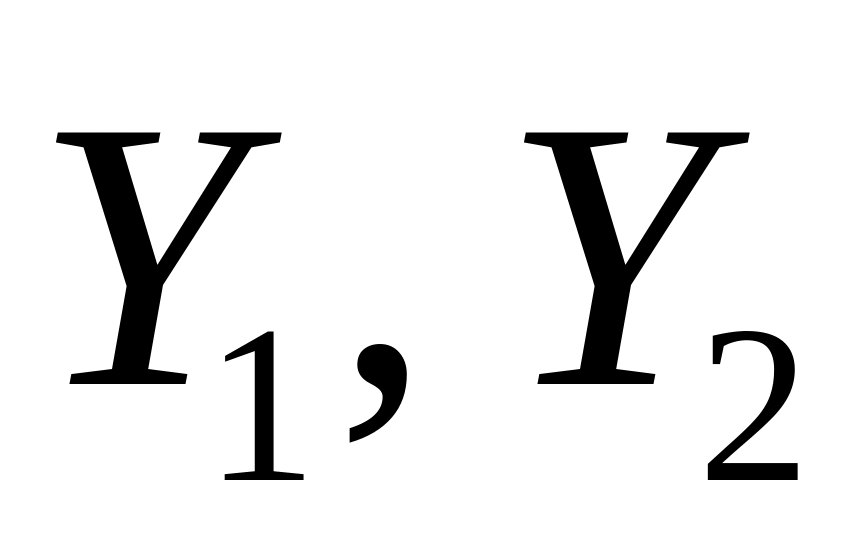независимы, и 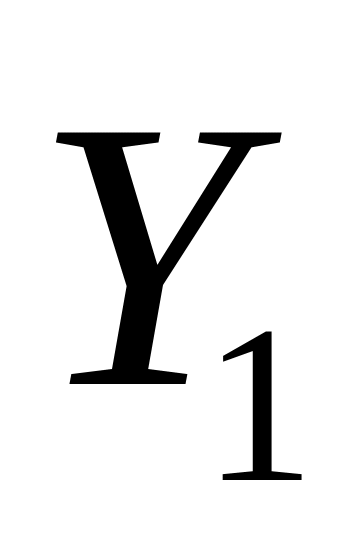~ 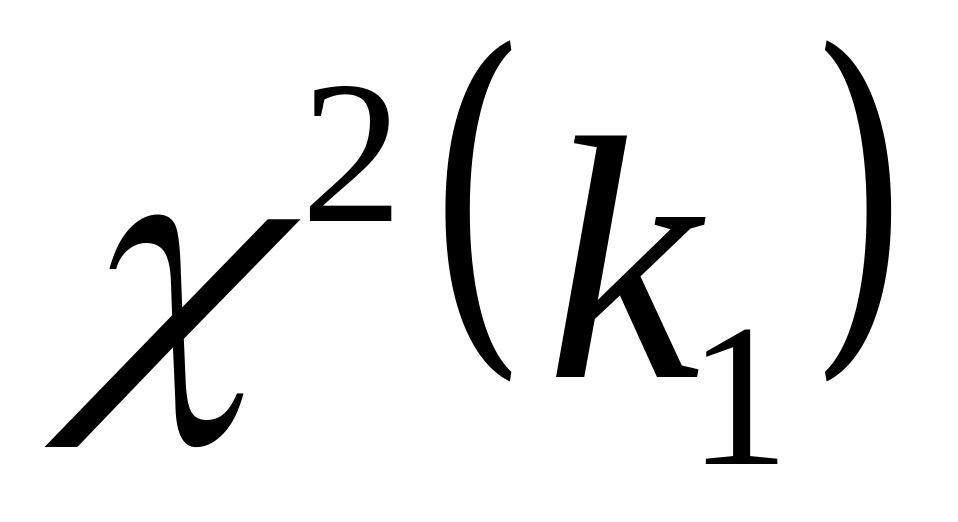, 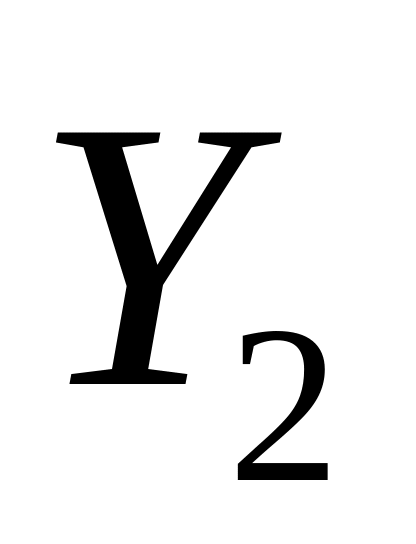~ 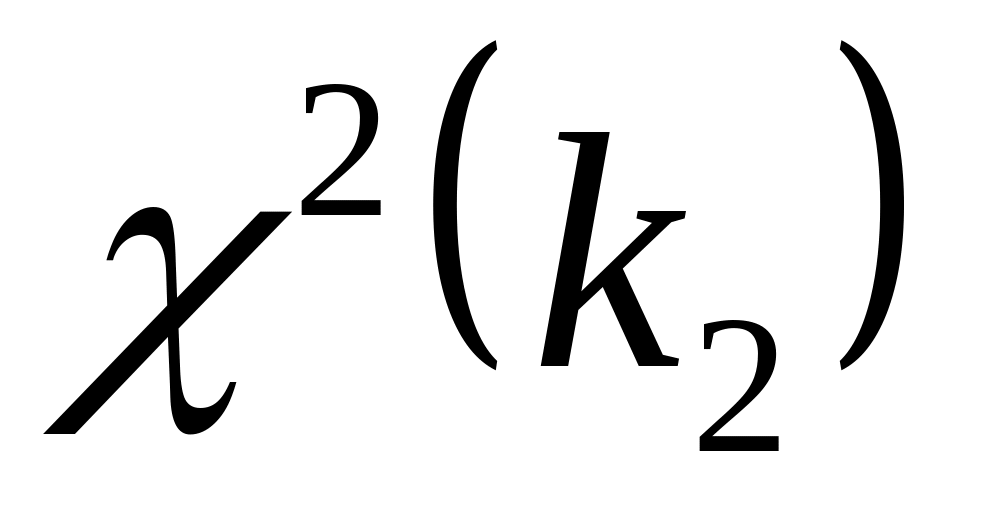, то ~ .

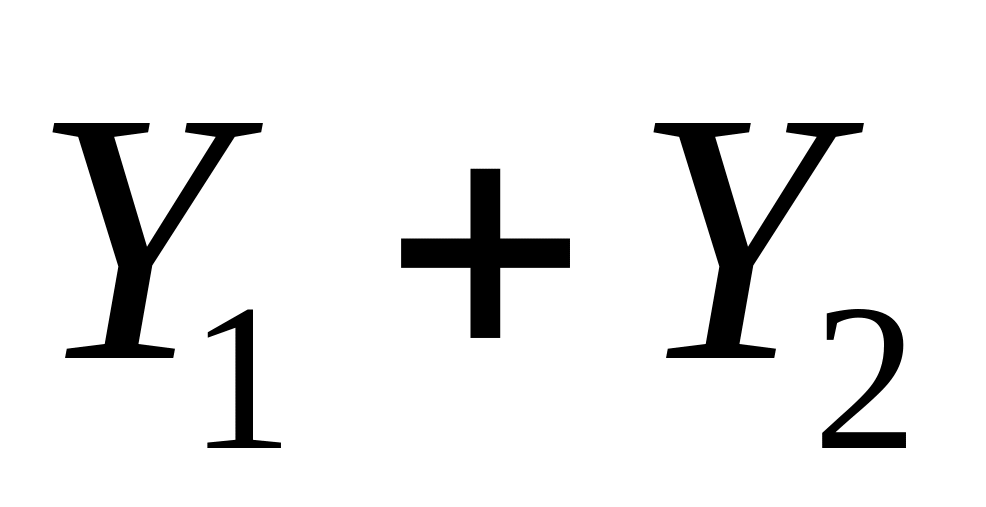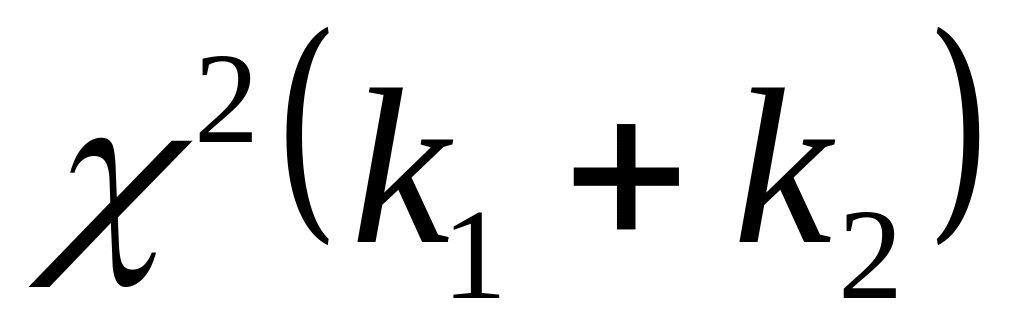2. Из определения легко получить моменты распределения . Если ~ 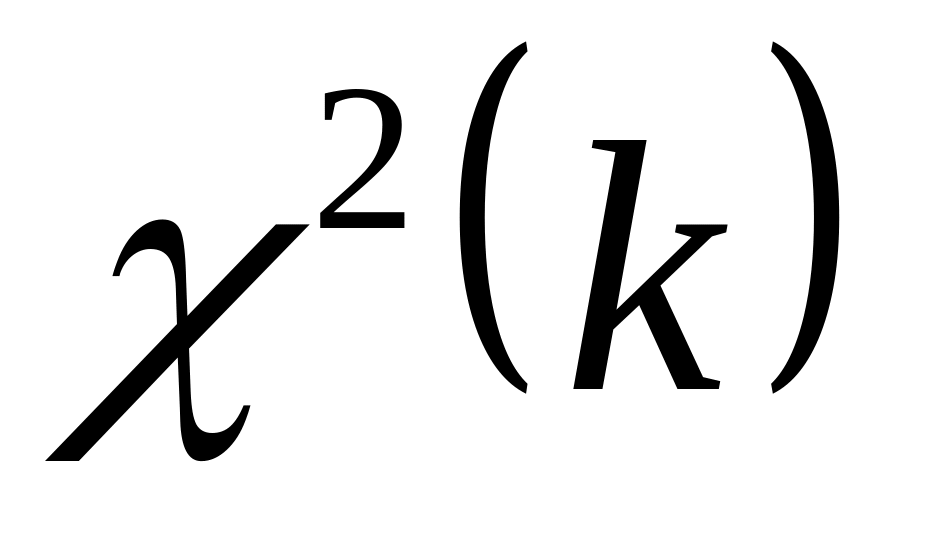, то

3. В силу центральной предельной теоремы, при большом числе степеней свободы распределение случайной величины ~ может быть приближено нормальным

.

Распределение Стьюдента. Данное распределение представляет собой однопараметрическое семейство абсолютно непрерывных распределений. Пусть независимые стандартные нормальные случайные величины, такие что ~ . Тогда распределение случайной величины , где

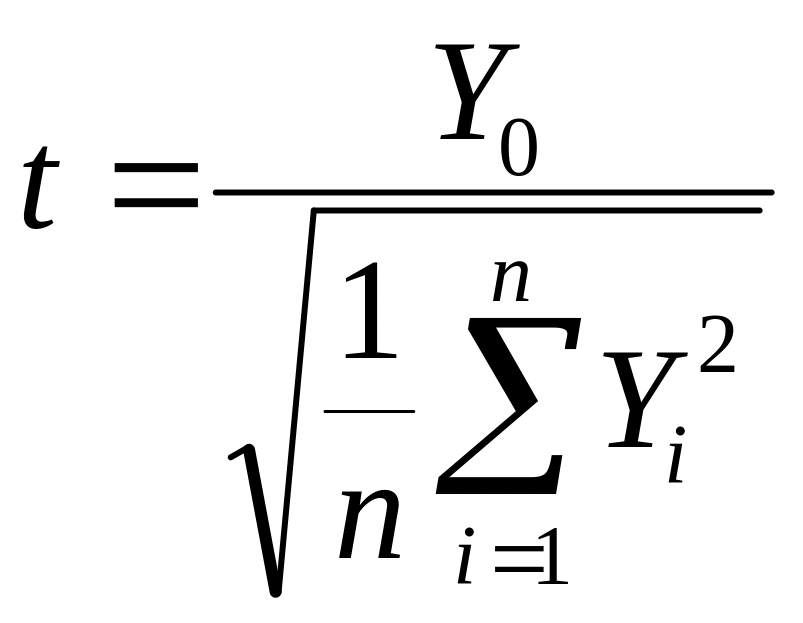
называется распределением Стьюдента с степенями свободы. Пишут ~ .

Плотность распределения имеет вид

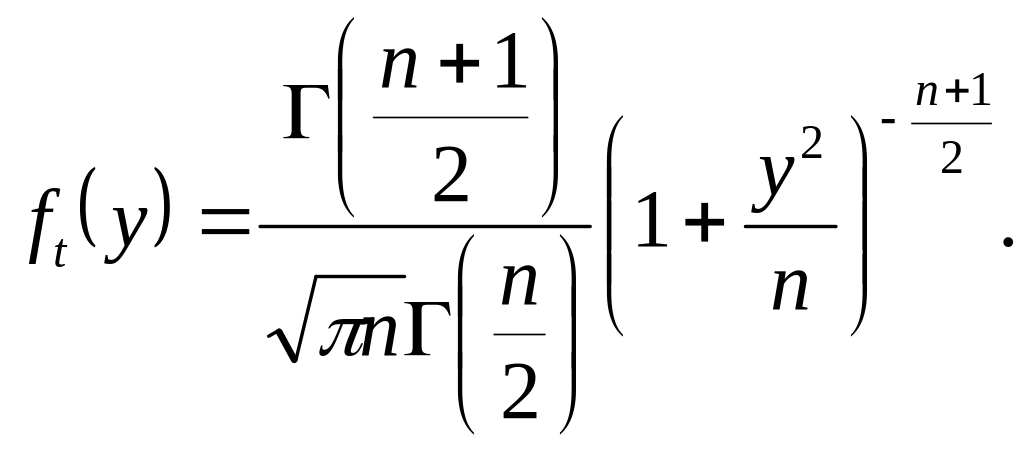
Свойства распределения Стьюдента.

1. Распределение Стьюдента симметрично. В частности, если ~ , то ~ .

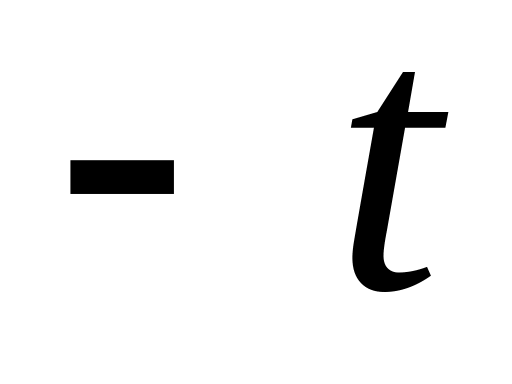2. Случайная величина ~ имеет только моменты порядков . Моменты порядков 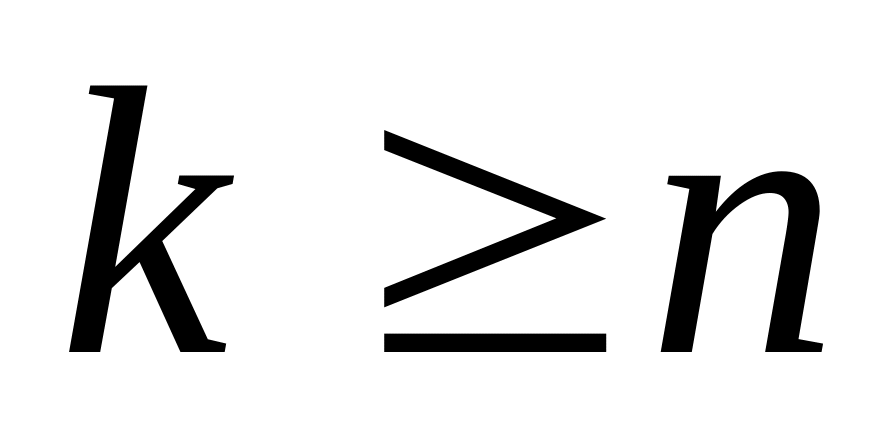не определены. В частности,

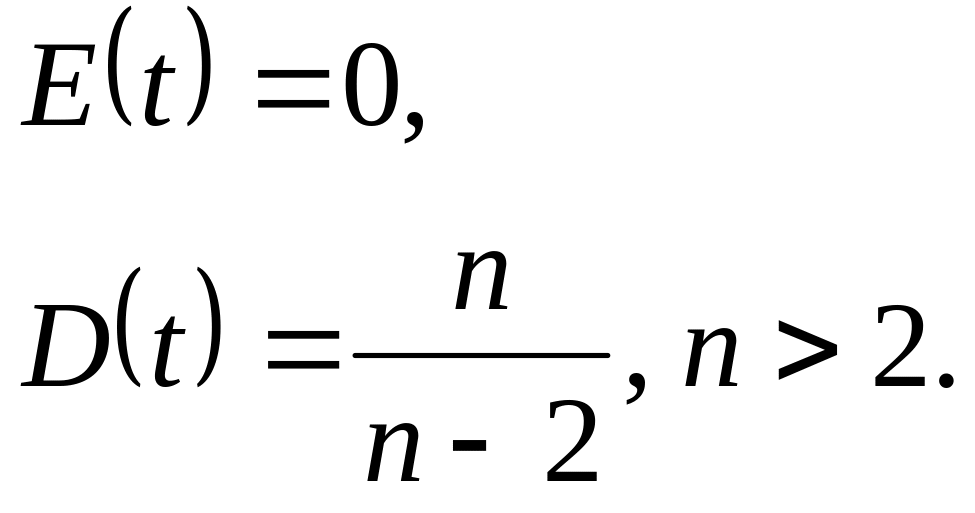
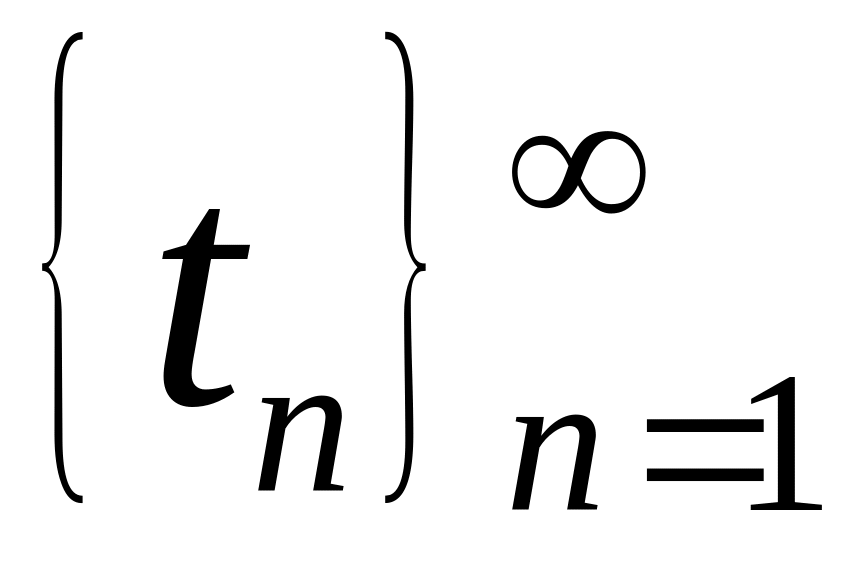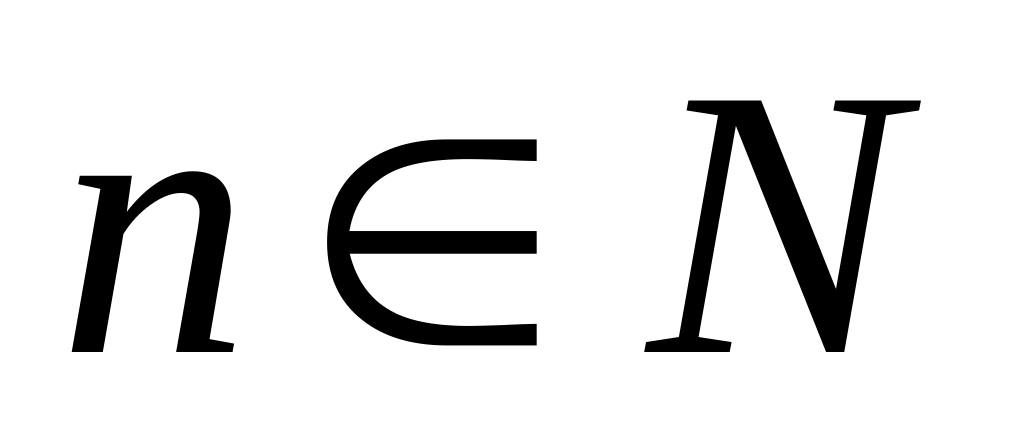3. Распределение Стьюдента сходится к стандартному нормальному при . Пусть дана последовательность случайных величин , где ~ , . Тогда 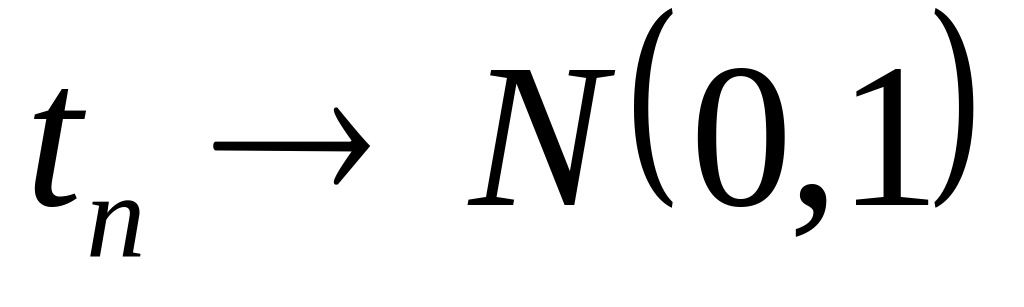по распределению при .

Распределение Стьюдента используется в статистике для точечного оценивания, построения доверительных интервалов и тестирования гипотез, касающихся неизвестного среднего статистической выборки из нормального распределения.

Техника работы с различными распределениями использует понятие производящей функции. При этом вид производящей функции однозначно определяет данное распределение.

Примеры с решениями

Пример 1. Найти производящую функцию нормально распределенной случайной величины , заданной плотностью распределения

.

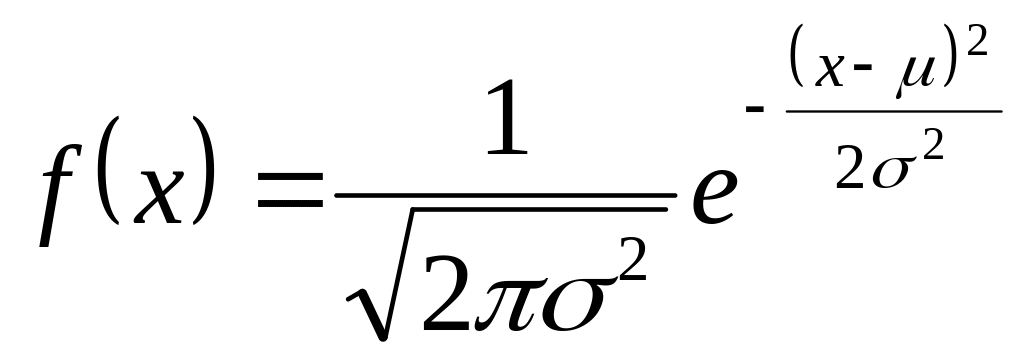Решение. .

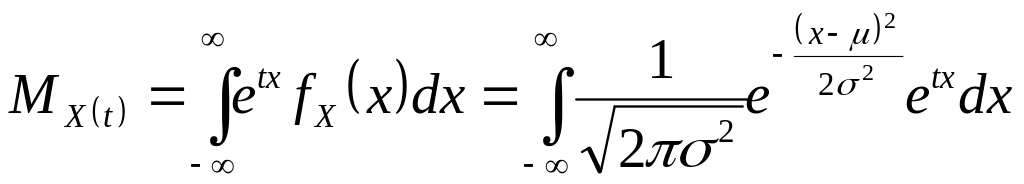Сделаем замену

Тогда

.

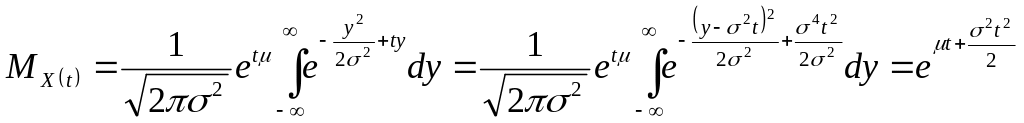Таким образом, производящая функция имеет вид

.

С помощью производящей функции найдем математическое ожидание

Задачи

Задача 1. С помощью производящей функции найти дисперсию нормально распределенной случайной величины , заданной плотностью распределения

.