
- •3. Расчет показателей безотказности невосстанавливаемых объектов для различных законов распределения
- •3.1. Показатели безотказности для экспоненциального распределения
- •3.2. Показатели безотказности для равномерного распределения
- •3.3. Показатели безотказности для усеченного нормального распределения
- •3.4. Показатели безотказности для распределения Вейбулла
3.3. Показатели безотказности для усеченного нормального распределения
Функция плотности распределения вероятностей классического нормального распределения записывается в виде:
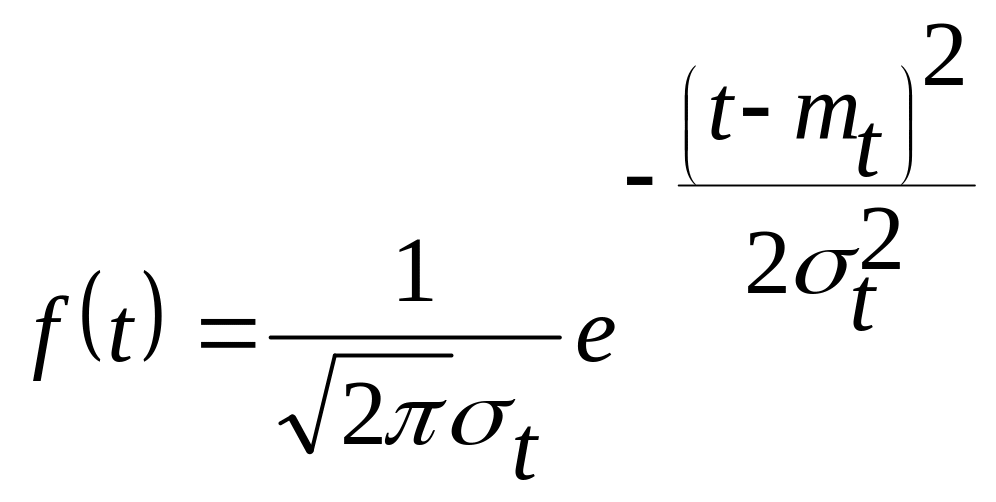 (3.6.)
(3.6.)
где: mt - математическое ожидание классического распределения;
t - среднеквадратическое отклонение.
Условие нормирования этой функции:
![]() (3.7)
(3.7)
Для случая t = mt :
![]()
Для
случая
![]() :
:
![]()

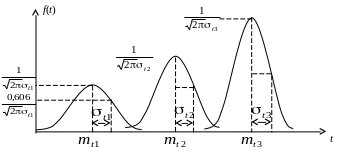 Рис.
4.3. Графики функций классического
нормального распределения при условии:
mt1<
mt2<
mt3
и
t3<t2<t1.
Рис.
4.3. Графики функций классического
нормального распределения при условии:
mt1<
mt2<
mt3
и
t3<t2<t1.
Поскольку случайная величина - наработка до отказа Т - теоретически изменяется в пределах от нуля до бесконечности, необходимо часть кривой распределения f(t), определяемой формулой (4.6.) для t<0 отсечь (т. е. устранить из рассмотрения). В этом случае имеет место усеченное нормальное распределение. Чтобы сохранить условие нормирования, а именно - площадь под кривой усеченного нормального распределения должна быть равна единице, вводится коэффициент усечения C0. Для нахождения коэффициента усечения С0 запишем условие нормирования:
![]() (3.8)
(3.8)
А коэффициент усечения равен:
 (3.9)
(3.9)
После ряда преобразований С0 равен:
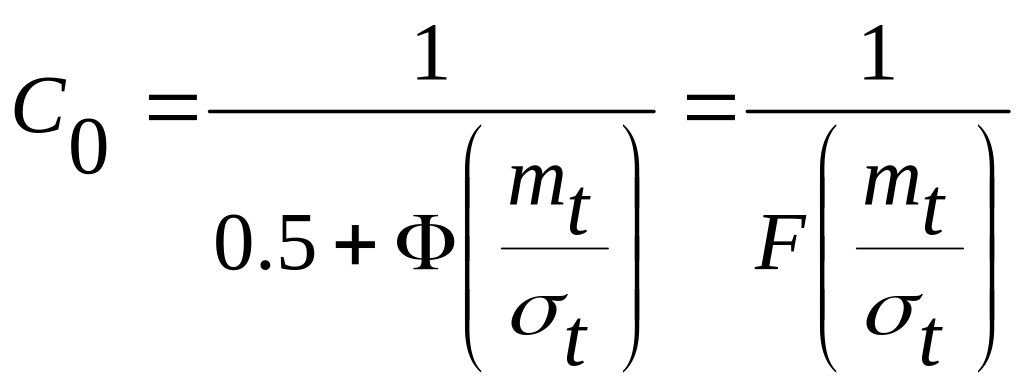 ,
(3.10.)
,
(3.10.)
где: Ф - нормированная функция Лапласа;
F - интеграл Лапласа.
Таблица 3.3.
Значения
С0
для разных отношений
|
|||||||
mt /t |
0,5 |
1,0 |
1,5 |
2,0 |
3,0 |
4,0 |
5,0 |
C0 |
1,446 |
1,186 |
1,071 |
1,023 |
1,001 |
1,0 |
1,0 |
Функция распределения наработки до отказа для усеченного нормального распределения:
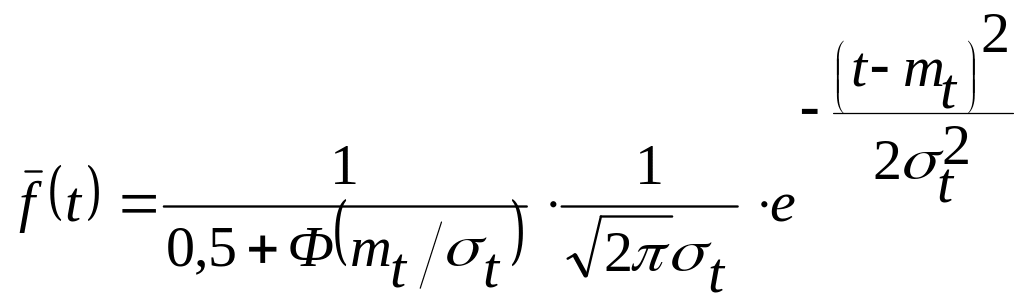 (3.11.)
(3.11.)
Вероятность безотказной работы и вероятность отказа с учетом (3.11.) и после преобразований запишем:
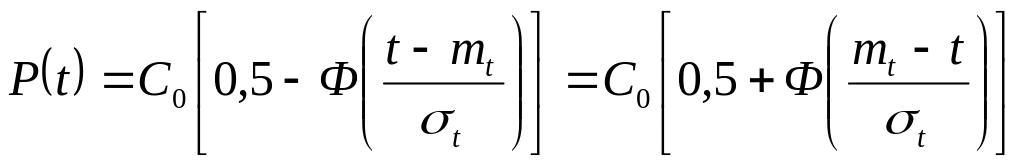
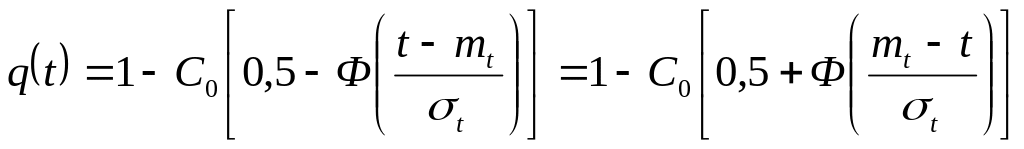 (3.12.)
(3.12.)
при
t
= mt
и при
![]()
![]() ,
т.к. Ф(0)=0
и С01,0
,
т.к. Ф(0)=0
и С01,0
Для
усеченного нормального распределения
на практике имеет место
T0mt,
если
![]() равенство P(t)
и q(t),
как и для равномерного распределения,
наступает при наработке, равной средней
наработке до отказа t=T0.
равенство P(t)
и q(t),
как и для равномерного распределения,
наступает при наработке, равной средней
наработке до отказа t=T0.
Таблица. 3.4.
Расчетные
значения P(t)
для двух
|
||||||
T |
0,5T0 |
0,7T0 |
T0 |
1,3T0 |
1,5T0 |
2T0 |
P(t)
|
0,7565 |
0,6882 |
0,4539 |
0,3258 |
0,2032 |
0,0651 |
P(t)
|
0,9937 |
0,9332 |
0,5 |
0,0668 |
0,0063 |
310-6 |
Данные таблицы показывают, что наибольшее число отказов происходит в интервале наработки от (T0-0,5t) до (T0+0,5t), т. е. при =1 наибольшее число отказов происходит в широком интервале наработки: от 0.9Т0 до 1.5Т0. В случае наибольшее число отказов происходит в значительно узком интервале наработки: от 0,9T0 до 1,1 T0.
Такой результат более предпочтителен, так как в более узком интервале наработки отказы становятся более вероятны, значит, легче организовать и обеспечить обслуживание и восстановление отказавших объектов.
0,5T0
T0
1,5
T0
2T0
0
t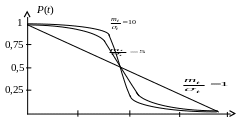
Рис.3.4 Графики P(t) для усеченного нормального распределения.
Интенсивность отказов усеченного нормального распределения найдем по формуле:
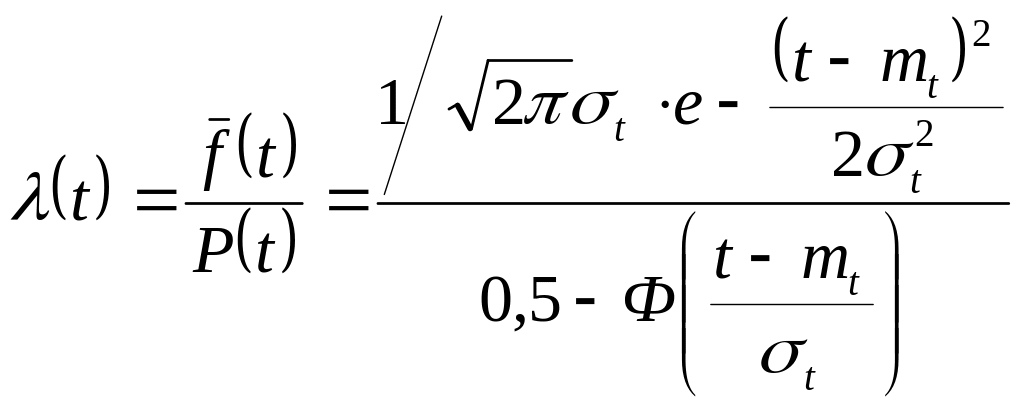 (3.13.)
(3.13.)
С
(t)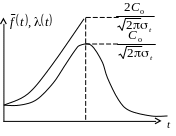
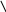 ростом наработки поведение кривой (t)
определяется как ходом функции
ростом наработки поведение кривой (t)
определяется как ходом функции
![]() усеченного нормального
распределения, так и ходом функции
надежности P(t).
усеченного нормального
распределения, так и ходом функции
надежности P(t).
(0)=f(0)
T0=mt
f(t)
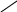
Рис.3.5
Графики функций
и (t)
для одного
значения отношения
![]() при
при
![]() .
.
При t=To и P(t=To)=0,5, (t=T0) равно удвоенному значению "высоты" функции и t>To интенсивность отказов увеличивается.
Средняя наработка до отказа определим по формуле:
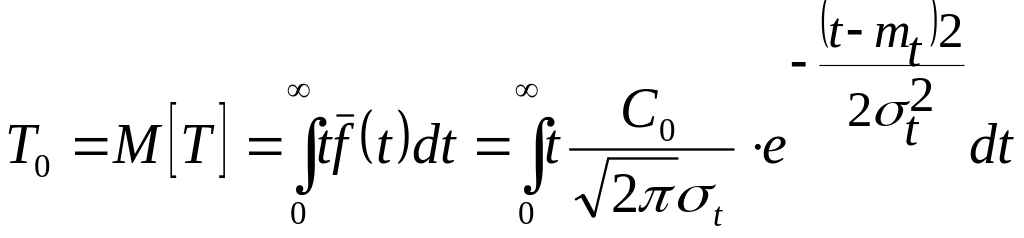 (3.14.)
(3.14.)
Проведя преобразование T0 формулы (3.14), получаем:
![]() где
(3.15.)
где
(3.15.)
![]()
Таблица 3.5.
Значения коэффициента К0 для разных отношений |
|||||||
|
0,5 |
1,0 |
1,5 |
2,0 |
3,0 |
4,0 |
5,0 |
К0 |
0,51 |
0,29 |
0,095 |
0,055 |
0,02 |
0,007 |
0,0026 |
T0/mt |
2,02 |
1,29 |
1,063 |
1,027 |
1,006 |
1,002 |
,10005 |
Из
Табл.3.5. видно, что превышение То
над
mt
существенно
при
![]() ,
а при
,
а при
![]() можно считать
.
можно считать
.
Усеченное
нормальное распределение имеет
среднеквадратические отклонения
![]() ,
отличное от
,
отличное от
![]() классического нормального распределения.
Для определения
найдем дисперсию наработки до отказа,
используя формулу (3.5):
классического нормального распределения.
Для определения
найдем дисперсию наработки до отказа,
используя формулу (3.5):
![]()
![]() (3.16.)
(3.16.)
Подставив в формулу (3.16) выражение (3.15) и проведя преобразование, получаем:
![]()
При
![]()
![]() ,
а
,
а![]()
При
![]()
![]() ,
а
,
а![]()
Следовательно,
при
![]()
![]()
Особенности усеченного нормального распределения следующие:
Для
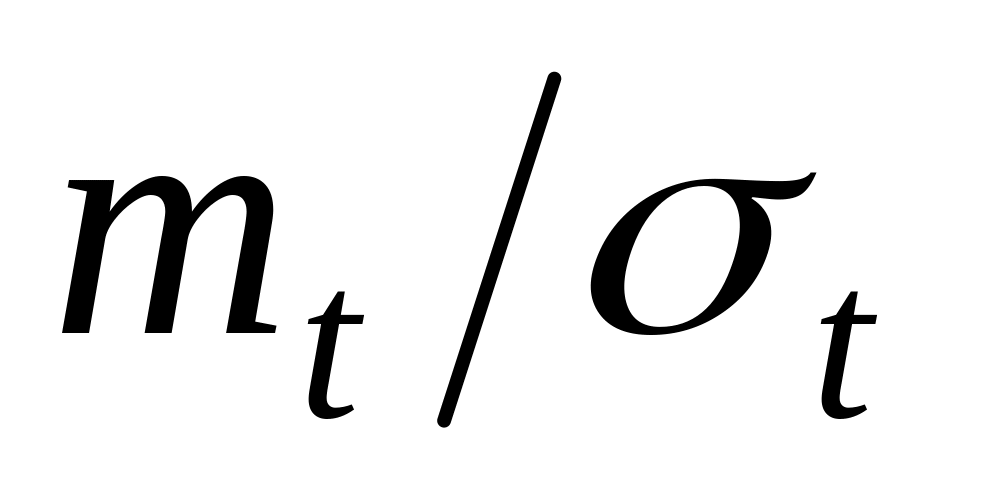 в пределах
3…10 число
отказов для объектов, находящихся под
наблюдением в интервале наработки
[0…(0,7….0,9)Т0]
увеличивается мало, достигая величины
порядка n(t) (0,07….0,1)N;
в пределах
3…10 число
отказов для объектов, находящихся под
наблюдением в интервале наработки
[0…(0,7….0,9)Т0]
увеличивается мало, достигая величины
порядка n(t) (0,07….0,1)N;Основное число объектов отказывает в интервале наработки (0,8…1,2)То при
 ;
;При t=T0 P(T0)=0,5, как в случае равномерного распределения - примерно половина объектов переходит в неработоспособное состояние;
При
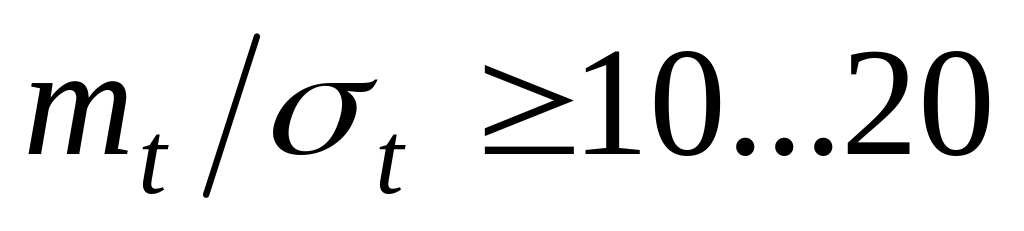 функция надежности приближается к
идеалу- релейной функции: Р(t)
резко падает от Р(t1)1,0
до Р(t2)0,
т. е. все объекты отказывают в узком
интервале наработки (t1….t2).
функция надежности приближается к
идеалу- релейной функции: Р(t)
резко падает от Р(t1)1,0
до Р(t2)0,
т. е. все объекты отказывают в узком
интервале наработки (t1….t2).
